Разработка нейро-нечеткого регулятора для противобуксовочной системы

DEVELOPMENT OF A NEURO-FUZZY CONTROLLER OF THE TRACTION CONTROL SYSTEM

Guzel Khairutdinova

Master, Naberezhnye Chelny Institute (branch) Federal State Autonomous Educational Institution of Higher Education K (P) FU, Russia, Naberezhnye Chelny

Аннотация. В данной работе представлена цифровая модель противобуксовчной системой (ПБС) с использованием нейро-нечеткого регулятора. Для выявления эффекта буксования анализируется разность угловых скоростей ведущих колес автомобиля  и для того чтобы устранить буксование на буксующем колесе будет уменьшаться подача передаваемого от двигателя крутящего момента.

Abstract. This article presents a digital model of a traction control system using a neuro-fuzzy controller. To identify the effect of skidding, the difference in angular speeds of the driving wheels of the car is analyzed and in order to eliminate skidding on the slipping wheel, the supply of torque transmitted from the engine will decrease.

Ключевые слова: противобуксовочная система, пробуксовка, прямолинейное движение автомобиля, ведущие колеса, ведомые колеса, нейро-нечеткий регулятор.

Keywords: traction control, slipping, rectilinear movement of the car, drive wheels, driven wheels, neuro-fuzzy regulator.

При составлении модели системы внешних сил и моментов, действующих на автомобиль при прямолинейном движении, примем следующие допущения:

• левые и правые колеса одноименных мостов имеют одинаковые нагрузки;
• конфигурация автомобиля изображается в виде плоской фигуры;
• опорная поверхность дороги представляется в виде прямой линии, наклоненной под малым углом   к горизонту;
• аэродинамическое сопротивление отсутствует;
• упругие свойства подвески не учитываются и колебания кузова не происходят.

Рассмотрим прямолинейное движение автомобиля (Рисунок 1).

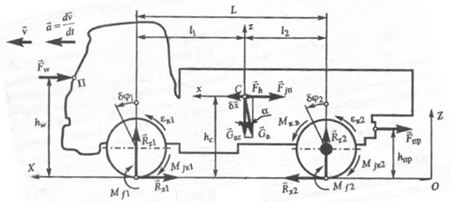
Рисунок 1. Воздействия на автомобиль при прямолинейном движении

Составим уравнение движения автомобиля:

,

где:  - скорость автомобиля вдоль горизонтальной оси;

 - горизонтальные реакции опорной поверхности дороги.

Рассмотрим колесо, катящееся по гладкой горизонтальной поверхности дороги с твердым покрытием в ведущем режиме (Рисунок 2).

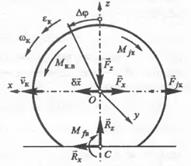
Рисунок 2. Система сил и моментов, действующих на ведущее колесо при движении

Составим общее уравнение динамики, согласно которому алгебраическая сумма работ всех внешних сил, приложенных к системе, равна нулю.

                                                                                               (1)

Рассмотрим колесо, катящееся по недеформируемой поверхности   (Рисунок 3) в ведомом режиме.

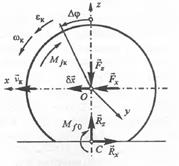
Рисунок 3. Система сил и моментов, действующих на ведомое колесо при движении

Составим общее уравнение динамики ведомого колеса аналогично случаю ведущего колеса. Получим:

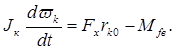                                                                                                        (2)

На основании, описанной выше, математической модели, создадим модель прямолинейного движения автомобиля в Matlab Simulink (рис 4).

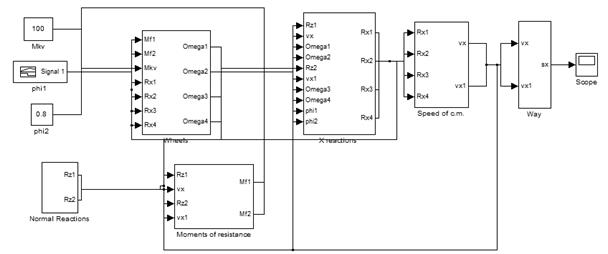
Рисунок 4. Модель прямолинейного движения автомобиля в Matlab Simulink

Подсистема «Wheels», построенная на основании формул (1) и (2), предназначена для расчета угловых скоростей колес правой и левой колеи автомобиля.

Подсистема «X Reactions» предназначена для расчета продольных реакций дороги.

Подсистема «Norm Reactions» предназначена для расчета нормальных реакций дороги

Подсистема «Moments of resistance» предназначена для расчета моментов сопротивления качению.

Подсистема «Speed of c.m.», предназначена для расчета скорости центра масс колей автомобиля.

Для выявления эффекта буксования будем анализировать разность угловых скоростей ведущих колес автомобиля. Пусть при превышении этой разности некоторого значения одно из колес начинает буксовать и для того чтобы устранить буксование на этом колесе необходимо уменьшить подачу передаваемого от двигателя крутящего момента.

На вход нечеткого регулятора (Рисунок 5) подается разность (w) угловых скоростей правого и левого ведущего колеса автомобиля. Нечеткий регулятор имеет два выхода:

• момент,  подводимый к левому колесу от двигателя через трансмиссию (Mkl);
• момент, подводимый к правому колесу от двигателя через трансмиссию (Mkr).

Рисунок 5. Нечеткий регулятор для ПБС

Диапазоны изменений значений термов для входных и выходных данных были установлены на основании исследовании построенной модели движения автомобиля.

Входная переменная имеет 5 термов, рассматривающих следующие соотношения угловых скоростей ведущих колес:

• угловая скорость левого ведущего колеса намного больше угловой скорости правого колеса (L>>R);
• угловая скорость левого ведущего колеса больше угловой скорости правого колеса (L>R);
• угловая скорость левого ведущего колеса приблизительно равна угловой скорости правого колеса (L~R);
• угловая скорость правого ведущего колеса больше угловой скорости левого колеса (L<R);
• угловая скорость правого ведущего колеса намного больше угловой скорости левого колеса(L<<R).

Рисунок 6. Графики функций принадлежности термов лингвистической переменной «W»

Выходные переменные имеют по 3 терма.

Рисунок 7. Графики функций принадлежности термов лингвистических переменных«Mkl» и «Mkr»

Нечеткие правила имеют следующий вид:

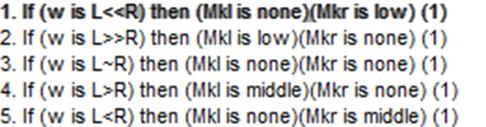
Рисунок 8. Нечеткие правила

Для проведения ряда экспериментов был выбран бортовой КАМАЗ-4308-Н3 (4х2) [4]. Примем следующие параметры:

масса автомобиля  ;

ускорение свободного падения  

приведенный к ведущему колесу суммарный момент инерции  колеса, двигателя и трансмиссии  

Так же для упрощения вычислений, будем считать, что:

• автомобиль движется с небольшой скоростью;
• деформация колеса при качении невелика (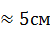) и радиус качения  не меняется с течением времени;
• коэффициент сопротивления качению является постоянной величиной ;
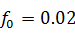• передаваемый от двигателя крутящий момент 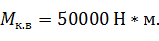 100 Н*м.

Для первого эксперимента, при прочих равных условиях, возьмем коэффициент сцепления 0.8 для левого колеса, а для правого представлен на рисунке ниже:

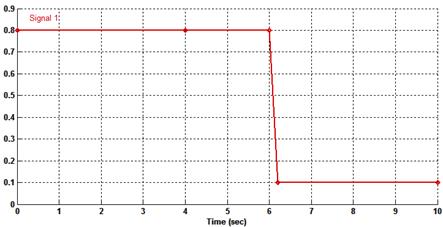
Рисунок 9. Коэффициент сцепления для правого колеса

Т.е. предполагаем, что правое колесо через ~6 секунд после начала движения попадает на обледенелый участок дороги и начинает буксовать.

Угловые скорости правого (синяя линия) и левого(зеленая линия) колеса до и после применения  ПБС представлены ниже:

Рисунок 10. Без использования ПБС

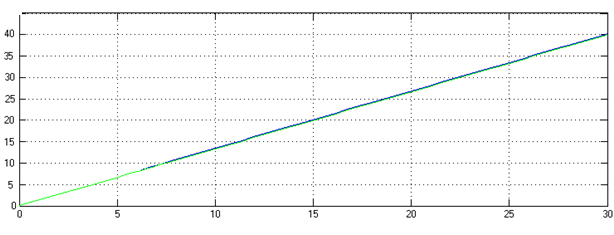
Рисунок 11. После применения ПБС

Для второго эксперимента, при прочих равных условиях, возьмем коэффициент сцепления   для правого колеса,  а для левого представлен на рисунке ниже:

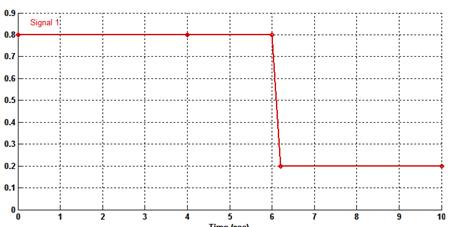
Рисунок 12. Коэффициентт сцепления для левого колеса

Угловые скорости левого(зеленая линия) и правого (синяя линия) колеса:

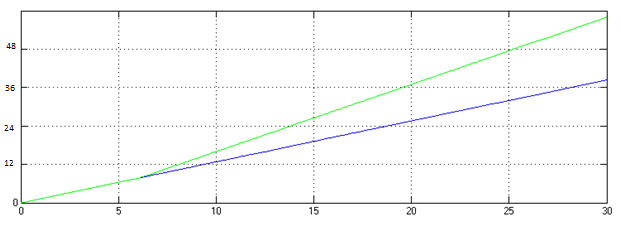
Рисунок 13. Без использования ПБС

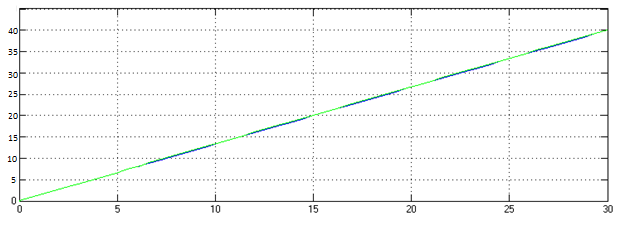
Рисунок 14. После применения ПБС

Главным достоинством данной модели является её простота. Так как в начальных условиях мы приняли, что автомобиль движется с небольшой скоростью по гладкой горизонтальной дороге.