Нелокальная задача для уравнения Лапласа в параллелепипеде

NONLOCAL PROBLEM FOR THE LAPLACE EQUATION IN A PARALLELEPIPED

Madinabonu Muxamadaliyeva

Undergraduate, Fergana state University, Uzbekistan, Fergana

Аннотация. Исследована нелокальная задача для уравнения Лапласа в прямоугольном параллелепипеде. Доказательство единственности решения и его построение проведены спектральным методом с использованием разложения в ряд Фурье. При некоторых условиях относительно параметров и заданных функций доказана равномерная сходимость построенного ряда.

Abstract. A nonlocal problem for the Laplace equation was investigated in a rectangular parallelepiped. The proof of the uniqueness of the solution and its construction was carried out by the spectral method, using Fourier series expansion. Under certain conditions, with respect to the parameters and given functions, the uniform convergence of the constructed series was proved.

Ключевые слова: уравнения Лапласа, нелокальная задача, спектральный метод, параллелепипед.

Keywords: Laplace equation, nonlocal problem, spectral method, parallelepiped.

1. Введение. Постановка задачи. В работе [1] А.А.Дезин исследовано уравнение  при граничном условии . Здесь предполагается, что для  функция  принимает значенные в комплексном банаховом пространстве , коммутирующий с  неограниченный линейный оператор с плотной областью определения и комплексное число, а также поясняется, что заданная условия «нелокальные» в том смысле, что задают связь между значениями неизвестной функции в различных точках границы.

Рассмотрим трехмерное уравнение Лапласа

,                                                                                                       (1)

для которого нелокальная задача исследуется в параллелепипеде

,

здесь неизвестная функция.

Рассмотрим следующую задачу и исследуем ее однозначную разрешимость.

Нелокальная задача. Найти функцию , удовлетворяющую уравнению (1) в области  и условиям

                                                                       (2)

, ,                                                                                 (3)

                                                                                      (4)

,                                                                                     (5)

где заданные непрерывные функции.

Краевые условия с локальным смещением (2) можно охарактеризовать следующим образом: условия (2) связывают значения искомого решения  и его производной на участках  и  границы  области .

2. Построение собственных функций

Для нахождения решения нелокальной задачи, применим метод Фурье, основанный на разделении переменных [11]. Найдем нетривиальные решения задачи (1)-(3). С этой целью, разделив переменные по формуле , из уравнения (1) получим

,                                                                                                  (6)

,                                                                                          (7)

где константа разделения.

Учитывая однородные условия (2) и (3), для уравнения (7) получим следующую задачу на собственные значения в области 

Задача . Найти значения параметра  и соответствующие им нетривиальные в  решения  уравнения (7), удовлетворяющие условиям

Путем разделения переменных  задача  сводится к следующим задачам на собственные значения для обыкновенных дифференциальных уравнений:

Задача: 

Задача:

где константа разделения.

Сначала найдем решение задачи . Нетрудно убедиться, что при  задача  не имеет нетривиальных решений. При  решением задачи  является функция  (постоянная). Если , то задача  имеет собственные значения . Следовательно, собственные значения  соответствующие этим собственным значениям, собственные функции задачи , представима в виде  и

.                                                                 (8)

Система собственных функций (8) ортогональна и полна в пространстве  и в нем образует ортонормированный базис [3].

Теперь перейдем к исследованию задачи . Рассмотрим уравнение  и найдем его общее решение. Уравнениа , удовлетворяющее условию , определяется равенством

.                                                                                                      (9)

Подставляя (9) в условие , получим условие существования нетривиального решения задачи :

                                                                                              (10)

Решая уравнения (10), находим те значения параметра , при которых существуют нетривиальные решения задачи :   где ,  .

Полагая в формуле (9) , , получим нетривиальные решения (собственные функции) задачи , с точностью до постоянного множителя:

                                                                                              (11) 

Согласно работе[3,4], система собственных функций (11) полна в .

Полагая в уравнении (6) , найдем его общее решение:

                                                                            (12)

здесь  и –произвольные постоянные.  

3. Единственность решения

Теперь переходим к доказательству единственности решения нелокальной задачи.

Теорема 1. Поставленная нелокальная задача не имеет более одного решения.

Доказательство. Пусть  и  есть решения задачи DZ. Тогда функция  удовлетворяет уравнению (1), условиям (2), (3) и однородным краевым условиям, соответствующим (4), (5). Докажем, что  в .

В области  справедливо тождество

.

Интегрируя это тождество по области

,

где  достаточно малые положительные числа, имеем

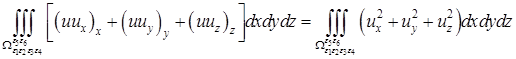.                                                                (14)

Если  стремится к нулю, то .

Применяя формулу Гаусса-Остроградского [2] к левой части равенства (14), после некоторых преобразований, имеем

.

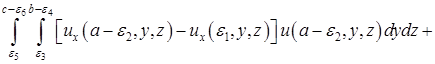
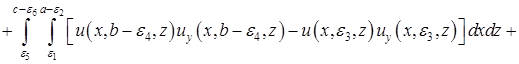
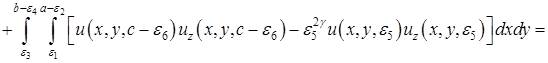
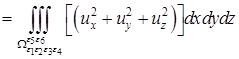Отсюда, переходя к пределу при  и однородные краевые условия получим

.

Следовательно, , . Тогда , . Так как  и , то , . Отсюда следует утверждение теоремы.

4. Построение и обоснование решение нелокальной задачи DZ

Решение нелокальной задачи в области  будем искать в виде

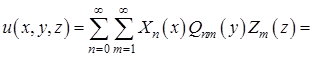
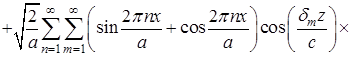
.                                                                                                     (15)

Каждый член ряда (15), удовлетворяет уравнению (1) и условиям (2) и (3). Предполагая, что этот ряд сходится абсолютно и равномерно, тогда постоянные  и  находим из требования, что функция (15) должно удовлетворять граничным условиям (4) и (5). Сначала, подставляя его в условия (4), получим

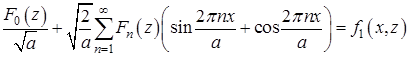,                                                                                   (16)

где 

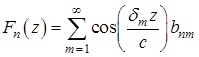.                                                                                                         (17)

Ряды (16) и (17) соответственно называются рядами Фурье функций  и  разложенной по системе тригонометрическим функциям. Из (16), коэффициенты Фурье определяется по формуле

,                                                                                                           (18)

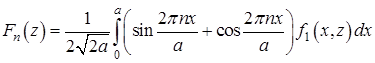.                                                                                    (19)

Так как  и  известны, поставляя их в (17), однозначно определяются  коэффициенты  и :

,    ,

где , .

Теперь подставляя функцию (15) в условие (5), имеем

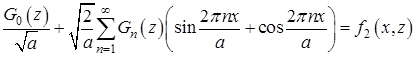,                                                                                (20)

где 

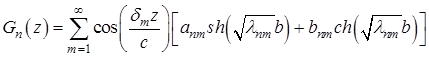.                                                                               (21)

Из (20) находим

, .

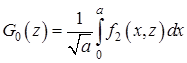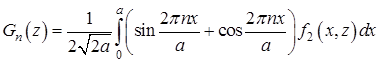Поставляя  и  в (21) получим

 ,

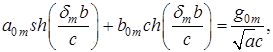
где , .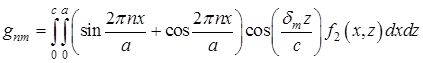

В силу известных коэффициентов  и  из последнего однозначно находим коэффициенты  и :

 .

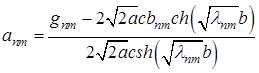Подставляя значения коэффициентов  и  в (15), находим формальное решение нелокальной задачи в виде

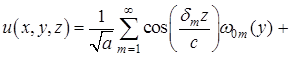
,                                                                          (22)

где

,

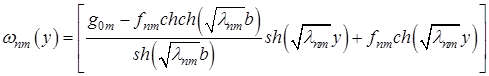      ,                                                                   (23)

Каждый член этого ряда удовлетворяет всем условиям нелокальной задачи. Отметим, что знаменатель коэффициентов ряда (22) не имеет нулей. Можно доказать, что ряд (15) и ряды , , , полученные из него дифференцированием, сходится равномерно в области их рассмотрения. Следовательно, его сумма будет решением нелокальной задачи.