ГЕНЕРАЦИЯ СИСТЕМ УРАВНЕНИЙ ПРИ РЕШЕНИИ ОДНОМЕРНЫХ ЗАДАЧ ДИРИХЛЕ И НЕЙМАНА МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Секция: 1. Математические науки

IV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: естественные и медицинские науки»
ГЕНЕРАЦИЯ СИСТЕМ УРАВНЕНИЙ ПРИ РЕШЕНИИ ОДНОМЕРНЫХ ЗАДАЧ ДИРИХЛЕ И НЕЙМАНА МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Постановка задачи. Рассмотрим краевую задачу
![]() для
для ![]() , (1)
, (1)
условия Дирихле:
![]() , (2)
, (2)
условия Неймана:
![]() (3)
(3)
Задачи (1), (2) и (1), (3) эквивалентны задаче минимизации функционала:
![]() (4)
(4)
Произведем разбиение ![]() с шагом
с шагом ![]() , получим сетку
, получим сетку ![]() . Приближенное решение ищем в виде линейной комбинации:
. Приближенное решение ищем в виде линейной комбинации:
![]() , (5)
, (5)
где коэффициенты ![]() — значения искомой функции в узлах сетки, а
— значения искомой функции в узлах сетки, а ![]() — финитные функции (базисные), заданные на разбиениях
— финитные функции (базисные), заданные на разбиениях ![]() такие, что
такие, что ![]() ,
, ![]() . Вид базисных функции [1, с. 101]:
. Вид базисных функции [1, с. 101]:
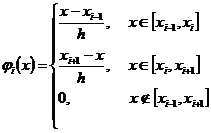 ,
, ![]() ,
,
 ,
, 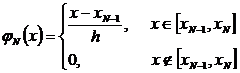 .
.
Геометрическая интерпретация базисных функций:

Рисунок 1. Графики базисных функций
Осуществляя переход от непрерывной задачи к конечномерной, подставляем (5) в (4). Для задач Дирихле и Неймана функционал принимает вид:
![]() ,
,
где: ![]() , а
, а 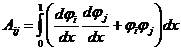 — элементы матрицы жесткости:
— элементы матрицы жесткости:
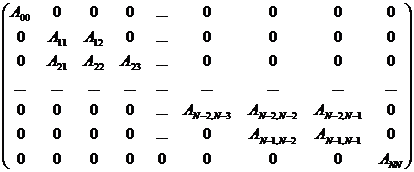 (6)
(6)
Учитывая необходимое и достаточное условие существования минимума выпуклого функционала, находим его вариацию и приравниваем ее к нулю. В результате получаем систему вида:
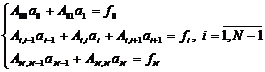 (7)
(7)
Для задачи Дирихле с однородными краевыми условиями ![]() матрица жесткости имеет вид:
матрица жесткости имеет вид:
 (8)
(8)
Соответствующая система уравнений:
 (9)
(9)
Для задачи Дирихле с неоднородными краевыми условиями ![]() матрица жесткости примет вид:
матрица жесткости примет вид:
 (10)
(10)
Соответствующая система уравнений:
 (11)
(11)
В задаче Неймана с однородными краевыми условиями ![]() значение функции на границе определяется следующим образом:
значение функции на границе определяется следующим образом:
![]()
Тогда матрица жесткости:
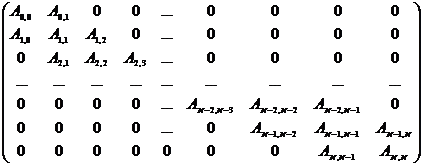 (12)
(12)
А соответствующая ей система примет вид:
 (13)
(13)
Для задачи Неймана с неоднородными краевыми условиями ![]() матрица жесткости имеет вид (12), система уравнений:
матрица жесткости имеет вид (12), система уравнений:
 (14)
(14)
где: ![]()
Так как матрицы коэффициентов систем имеют трехдиагональный вид, то целесообразно решать их методом прогонки.
Пример 1. Найти непрерывную на ![]() функцию
функцию  удовлетворяющую уравнению
удовлетворяющую уравнению ![]() и краевым условиям
и краевым условиям ![]() .
.
В результате решения данной краевой задачи при ![]() получаем:
получаем:
![]() ,
, ![]() .
.
Базисные функции: ![]()
 ;
;  ;
; 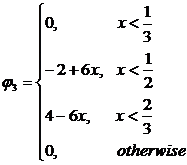 ;
;
 ;
;  .
.
В матрице жесткости элементы главной диагонали равны ![]() , поддиагональ и наддиагональ состоит из элементов
, поддиагональ и наддиагональ состоит из элементов ![]() . Правые части системы:
. Правые части системы:
![]()
В результате решения получаем искомые коэффициенты:
![]()
Приближенное решение имеет следующий вид:
![]()
График приближенного решения представлен на рисунке 2.

Рисунок 2. График решения задачи Дирихле с однородными краевыми условиями
Пример 2. Найти решение задачи Дирихле на ![]() для уравнения
для уравнения ![]() и краевых условий
и краевых условий ![]() Значения
Значения ![]() такие же как в примере 1. Базисные функции, для узлов
такие же как в примере 1. Базисные функции, для узлов ![]() и
и ![]() :
:
 ;
; 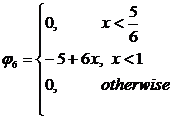 .
.
В матрице жесткости ![]() элементы на главной диагонали равны
элементы на главной диагонали равны ![]() , а поддиагональные и наддиагональные элементы равны
, а поддиагональные и наддиагональные элементы равны ![]() .
.
Правые части системы:
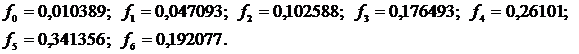
Искомые коэффициенты:
![]()
Приближенное решение имеет следующий вид:

График приближенного решения представлен на рисунке 3.
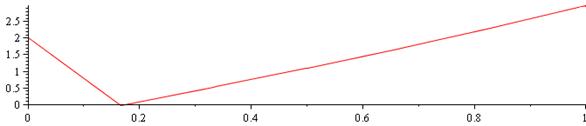
Рисунок 3. График решения задачи Дирихле с неоднородными краевыми условиями
Пример 3. Найти на ![]() функцию
функцию ![]() удовлетворяющую уравнению
удовлетворяющую уравнению ![]() и краевым условиям
и краевым условиям ![]() Значения
Значения ![]()
как в примере 2.
В матрице жесткости ![]() диагональные элементы равны
диагональные элементы равны ![]() , поддиагональные и наддиагональные
, поддиагональные и наддиагональные ![]()
![]() .
.
Правые части системы:
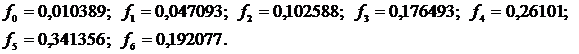
Получаем коэффициенты:
![]()
Приближенное решение имеет следующий вид:

![]()
График приближенного решения представлен на рисунке 4.

Рисунок 4. График решения задачи Неймана с однородными краевыми условиями
Пример 4. Найти на ![]() функцию
функцию ![]() удовлетворяющую уравнению
удовлетворяющую уравнению ![]() и краевым условиям
и краевым условиям ![]() Значения
Значения ![]()
как в примере 3.
В матрице жесткости ![]() диагональные элементы равны
диагональные элементы равны ![]() , поддиагональные и наддиагональные
, поддиагональные и наддиагональные ![]()
![]() .
.
Правые части системы:
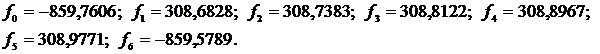
Получаем коэффициенты:
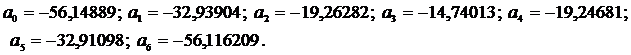
Приближенное решение имеет следующий вид:
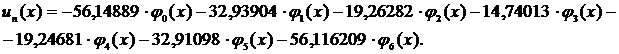
График приближенного решения представлен на рисунке 5.

Рисунок 5. График решения задачи Неймана с неоднородными краевыми условиями
Список литературы:
1. Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. — М.: Наука. Главная редакция физико-математической литературы, 1981. — 416 с.





