РЕШЕНИЕ МАТРИЧНЫХ ИГР

В практической деятельности часто приходиться рассматривать явления и ситуации, в которых участвуют две и более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления принято называть конфликтами. Конфликтная ситуации, взятая из жизни, довольно сложна. К тому же её изучение затруднительно наличием многих разных обстоятельств, часть из которых не оказывает существенного влияния на развитие конфликта или на его исход. Поэтому, для того что бы анализ конфликтной ситуации оказался возможным, необходимо отвлечение от второстепенных факторов, при удачном стечении обстоятельств позволяющее построить упрощенную формализованную модель конфликта, которую принято называть игрой. От реальной конфликтной ситуации её отличает то, что она ведется по определенным правилам.

Рассмотрим основные термины. Заинтересованные стороны являются игроками. Любое возможное для игрока действие является стратегией. Набор стратегий, называется ситуацией. Число, выражающее степень удовлетворения интересов игрока, является выигрышем.

Классификация, по виду функций выигрышей игры делятся:

1)  Матричные.

2)  Биматричные.

3)  Игры типа дуэль.

4)  Непрерывные.

5)  Выпуклые.

6)  Позиционные.

В моем докладе мы рассмотрим самые простые виды игр — матричные.

Матричные игры моделируют основные ситуации, в которых каждая из сторон-участниц делает свой ход одновременно со второй стороной.

Рассмотрим основные понятия матричных игр.

Рассмотрим игру, в которой участвуют 2 игрока, причем каждый из игроков имеет конечное число стратегий. Для удобства обозначим их как A и B. Предположим, что игрок А имеет m стратегий, а игрок B — n стратегий. Будем считать что выигрыш игрока А со стратегий Аik равен выигрышу игрока Bik или проигрышем. Тогда если нам известны значения aik, выигрыша при каждой паре стратегий, то их удобно записать в виде матрицы.

Полученная матрица имеет размер m x n и называется матрицей игры или платежной матрицей.

Оптимальная стратегия — это стратегия при многократном повторении которой отказ от выбранной стратегии одним из игроков увеличивает его шансы на проигрыш. В теории игр предполагается, что каждый из игроков стремиться к максимальному выигрышу, считая что соперник действует наилучшим для себя образом.

Таблица 1.

Действия игроков А и B при оптимальных стратегиях

Если α=β, то ситуация оказывается равновесной, и ни один из игроков не заинтересован в том, чтобы её нарушить. Если нижняя цена игры равна верхней цене игры, то общее значение называется ценой игры и обозначается ν.

В случае если α<β, уже нельзя говорить о равновесной игре и стоит говорить о смешанных стратегиях.

Смешанная стратегия — это случайная величина, значением которой являются стратегии игрока. Задание смешанной стратегии игрока состоит в указании вероятностей, с которыми выбираются его первоначальные стратегии. Рассмотрим матрицу m x n.

Сумма чистых стратегий игрока А равна 1.

Сумма чистых стратегий игрока В равна 1.

Задав 2 набора P={p₁, p₂, …, p_m} и Q={q₁, q₂, …,q_n} мы оказываемся в ситуации смешанных стратегий.

Величина ν=H_A(P⁰,Q⁰) является ценой игры. А набор (P⁰, Q⁰, ν), называется решением матричной игры.

Методы решения матричных игр.

Игры 2 x n.

Предположим что игрок А выбрал смешанную стратегию P={p,1-p}, а игрок В чистую стратегию k=1,2,…,n. Тогда средний выигрыш игрока А в ситуации {P,k} оказывается равным w=a_ikp+a_2k(1-p), на плоскости это уравнение описывает прямую, тем самым каждой чистой стратегии игрока В соответствует своя прямая. Поэтому на плоскости (p,w) рисуем все прямые w=a_ikp+a_2k(1-p), k=1,2, …, n. Затем на каждой из построенных прямых определяется и отмечается наименьшее значение. В результате должна получиться ломаная, которая огибает снизу все семейство построенных прямых. Данная кривая является нижней огибающей. Верхняя точка нижней огибающий определяет цену игры — ν и оптимальную стратегию игрока А — P⁰={p⁰,1-p⁰}.

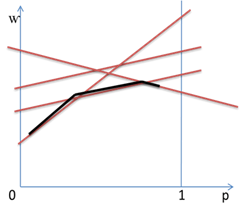
Игры m x 2.

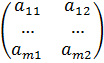
Пусть Q={q,1-q} — произвольная смешанная стратегия игрока В. Если игрок А выбирает i-ю чистую стратегию, i=1,2, …, m, то средний выигрыш игрока В в ситуации {I,Q} будет равен w=a_i1q+a_i2(1-q), i=1,2, …,m. Аналогично строим прямые, но теперь находим максимальные значения. В результате получается ломаная — верхняя огибающая. Абсциссой нижней точки полученной ломаной будет значение q⁰, определяющие оптимальную смешанную стратегию игрока B, а ординатой w⁰ — цена игры.

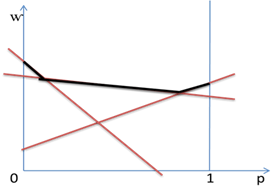
Игры m x n.

Решение любой матричной игры можно свести к решению матриц 2 x n и m x 2.

Рассмотрим несколько правил, помогающих решать матричные игры.

Правило доминирования.

Произвольная матрица.

Будем говорить, что i-я строка матрицы А (a_i1 a_{i2 …} a_in) не больше j-й строки этой матрицы (a_j1 a_{j2 …} a_jn), если одновременно выполнены следующие n неравенств — a_{i1 ≤} a_j1, a_{i2 ≤} a_{j2, …} a_{in ≤} a_jn. При этом говорят, что j-я строка доминирует i-ю строку, или что стратегия A_j игрока А доминирует стратегию A_i. Если в матрице А строка доминирует другую строку, то число строк можно уменьшить путем отбрасывания доминируемой строки.

Рассмотрим случай когда k-й (a_1k, a_2k, …, a_mk) столбец матрицы А не меньше l-го (a_1l, a_2l, …, a_ml) столбца этой матрицы, если одновременно выполнены следующие m неравенствa a_1k ≥ a_1l, a_2k ≥ a_2l, …, a_mk ≥ a_ml. При этом говорят, что l-й столбец доминирует k-й столбец, или что стратегия B_l игрока В доминирует стратегию B_k. Если в матрице А один из столбцов доминирует другой столбец, то число столбцов в матрице А можно уменьшить путем отбрасывания доминируемого столбца.

Аффинное правило. (Допустимые преобразования матрицы игры и её цена).

Оптимальные стратегии у матричных игр, элементы матриц А и С которые связаны равенством с_ik=a_ik+µ, i=1,2,…,m; k=1,2,…,n, где λ>0, а µ — произвольно, имеют одинаковые равновесные ситуации, а их цены удовлетворяют следующему условию ν_с=ν_А+µ.

Рассмотрим пример матричной игры.

«Рейтинг-план студента».

Рассмотрим рейтинг-план студента по некоторому предметы.

Предположим, что платежная матрица, отражающая интересы договаривающихся сторон, имеет следующий вид

Матрица описывает результаты студента (игрок А) и баллы преподавателя (игрок В). Первая строка это баллы студента, которые он получил за первый модуль, Первый столбец — баллы преподавателя, которые можно максимально получить за первый модуль. Вторая строка показывает баллы студента за второй модуль, а второй столбец баллы, которые готов поставить преподаватель за второй модуль и так далее аналогично.

Студент стремиться максимизировать свои баллы, в то время как преподавателю хотелось бы минимизировать баллы для того что бы студент учился еще лучше.

В данной задаче нас интересует вопрос, хватит ли студенту баллов для получения зачета?

Нетрудно заметить, что седловой точки у платежной матрицы нет. Кроме того, для дальнейшего анализ существенными являются лишь стратегии А₁ и А₄ игрока А и стратегии В₃ и В₄ игрока В. (в этом нетрудно убедиться, воспользовавшись правилом доминирования стратегий) В результате соответствующего усечения получим матрицу

Воспользовавшись аффинным правилом

65=5·4+45; 45=5·0+45; 50=5·1+45; 55=5·2+45,

Получаем новую матрицу