КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ АЛГЕБР СИММЕТРИИ УРАВНЕНИЯ КЛЕЙНА-ГОРДОНА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
Секция: 3. Физические науки
лауреатов
участников
лауреатов


участников



XXIV Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: естественные и медицинские науки»
КЛАССИФИКАЦИЯ ТРЕХМЕРНЫХ АЛГЕБР СИММЕТРИИ УРАВНЕНИЯ КЛЕЙНА-ГОРДОНА В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
В настоящей работе рассматривается уравнение Клейна-Гордона для заряженной массивной частицы во внешнем электромагнитном поле. Так как это уравнение не решается в общем случае, предлагается построить операторы симметрии для этого уравнения. Для этого строятся генераторы алгебры симметрии, затем находится 2-форма электромагнитного поля, с помощью которой можно построить операторы симметрии. В заключении работы мы анализируем полученную алгебру операторов симметрии уравнения Клейна-Гордона во внешнем электромагнитном поле и сравниваем ее с алгеброй Пуанкаре — алгеброй симметрии уравнения Клейна-Гордона для свободной заряженной частицы.
Рассмотрим уравнение Клейна-Гордона для свободной заряженной частицы массой ![]() :
:
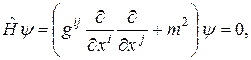 (1)
(1)
где: ![]() — оператор Гамильтона;
— оператор Гамильтона;
![]() — волновая функция частицы;
— волновая функция частицы;
![]() — ковариантный метрический тензор пространства-времени Минковского.
— ковариантный метрический тензор пространства-времени Минковского.
Операторы симметрии первого порядка ![]() уравнения (1) удовлетворяют следующему коммутационному соотношению [1]:
уравнения (1) удовлетворяют следующему коммутационному соотношению [1]:
![]() (2)
(2)
Известно, что такие операторы симметрии образуют алгебру Ли ![]() группы Пуанкаре со следующими генераторами:
группы Пуанкаре со следующими генераторами:
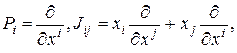 (3)
(3)
где: ![]() — генераторы сдвигов;
— генераторы сдвигов;
![]() — генераторы вращений.
— генераторы вращений.
Во внешнем электромагнитном поле с потенциалом ![]() уравнение (1) принимает вид:
уравнение (1) принимает вид:
![]() (4)
(4)
где: 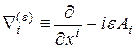 ;
;
![]() — заряд частицы.
— заряд частицы.
Будем рассматривать операторы симметрии уравнения (4) в виде:
![]() (5)
(5)
где: ![]() — неизвестные функции.
— неизвестные функции.
Учитывая потенциал внешнего поля ![]() , найдем вид функций
, найдем вид функций ![]() .
.
Операторы симметрии (5) удовлетворяют следующему коммутационному соотношению:
![]() (6)
(6)
Условие (6) равносильно системе уравнений:
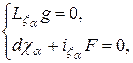 (7)
(7)
где: ![]() — замкнутая 2-форма внешнего электромагнитного поля;
— замкнутая 2-форма внешнего электромагнитного поля;
![]() — производная Ли вдоль векторного поля
— производная Ли вдоль векторного поля ![]() ;
;
![]() — оператор внутреннего произведения.
— оператор внутреннего произведения.
Уравнения (7) также приведены в работе [2], но структура алгебры операторов симметрии в этой работе не изучается.
Решение первого уравнения системы (7) — это вектора Киллинга вида (3). Отберем из них те векторы, которые сохраняют 2-форму ![]() внешнего электромагнитного поля, то есть удовлетворяющие условию:
внешнего электромагнитного поля, то есть удовлетворяющие условию:
![]() (8)
(8)
Множество таких векторов образует некоторую подалгебру ![]() в алгебре
в алгебре ![]() .
.
Решая второе уравнение системы (7) с полученными векторами ![]() , находим:
, находим:
![]() (9)
(9)
Интеграл в (9) корректен в силу условия (8).
Используя найденные функции ![]() строим операторы симметрии первого порядка уравнения Клейна-Гордона согласно (5). Данные операторы образуют некоторую алгебру
строим операторы симметрии первого порядка уравнения Клейна-Гордона согласно (5). Данные операторы образуют некоторую алгебру![]() , в общем случае отличную от алгебры Пуанкаре
, в общем случае отличную от алгебры Пуанкаре ![]() .
.
Изучим структуру алгебры ![]() . Коммутатор
. Коммутатор ![]() и
и ![]() можно записать как
можно записать как
![]() (10)
(10)
где: ![]() — структурные константы алгебры
— структурные константы алгебры ![]() ;
;
![]() имеет вид:
имеет вид:
![]() (11)
(11)
Можно показать, что ![]() образует 2-коцикл алгебры Ли
образует 2-коцикл алгебры Ли ![]() [3]. Видно, что в общем случае алгебра
[3]. Видно, что в общем случае алгебра ![]() неизоморфна алгебре
неизоморфна алгебре ![]() .
.
Если найдутся постоянные ![]() такие, что
такие, что
![]() (12)
(12)
тогда
![]() (13)
(13)
Таким образом новые операторы симметрии
![]() (14)
(14)
образуют алгебру Ли изоморфную алгебре ![]() :
:
![]() (15)
(15)
Коцикл ![]() вида (12) называется тривиальным.
вида (12) называется тривиальным.
Из (15) нетрудно заметить, что в случае тривиального коцикла ![]() «включение» внешнего поля не влияет на структуру алгебры операторов симметрии.
«включение» внешнего поля не влияет на структуру алгебры операторов симметрии.
Для иллюстрации приведенного выше алгоритма рассмотрим трехмерную подалгебру ![]() алгебры Пуанкаре
алгебры Пуанкаре ![]() со следующими коммутационными соотношениями:
со следующими коммутационными соотношениями:
![]() (16)
(16)
Рассмотрим уравнение (4) с потенциалом внешнего электромагнитного поля
![]() (17)
(17)
где: ![]() — произвольная функция;
— произвольная функция;
![]() — произвольная постоянная.
— произвольная постоянная.
Данному потенциалу соответствует 2-форма ![]()
Решая первое уравнение системы (7) совместно с условием (8), получаем векторы Киллинга:
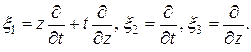 (19)
(19)
Тем самым, найдены искомые функции ![]()
Используя найденные векторы Киллинга, находим следующие функции ![]() :
:
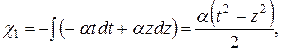 (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
Теперь мы можем построить операторы симметрии уравнения Клейна-Гордона во внешнем электромагнитном поле:
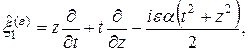 (23)
(23)
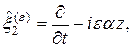 (24)
(24)
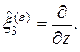 (25)
(25)
Запишем ненулевые коммутаторы операторов симметрии (23) — (25), учитывая структурные константы (17) алгебры ![]() :
:
![]() 26)
26)
![]() (27)
(27)
![]()
![]() (28)
(28)
Из (26) — (28) находим коцикл, учитывая свойство кососимметричности ![]() :
:
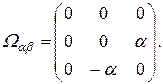 (29)
(29)
Поскольку ![]() то невозможно найти такие величины
то невозможно найти такие величины ![]() , что
, что
![]() (30)
(30)
и, следовательно, 2-коцикл (29) является нетривиальным. Операторы (23) — (25) образуют алгебру симметрии неизоморфную исходной подалгебре ![]() уравнения Клейна-Гордона (1).
уравнения Клейна-Гордона (1).
В настоящей работе были построены операторы симметрии уравнения Клейна-Гордона для заряженной массивной частицы в электромагнитном поле. Выяснилось, что алгебра операторов симметрии данного уравнения в общем случае неизоморфна алгебре Пуанкаре, образованной операторами симметрии уравнения Клейна-Гордона для свободной частицы. Сохранение симметрий уравнения при «включении» внешнего поля определяется тривиальностью соответствующего 2-коцикла. Для всех трехмерных подалгебр алгебры Пуанкаре, в соответствие с изложенным в настоящей работе алгоритмом, были построены операторы симметрии первого порядка, приведен пример их вычисления для одной из подалгебр.
Список литературы:
1. Фущич В.И., Никитин А.Г. Симметрия уравнений квантовой механики. — 1990.
2. Van Holten J.W. Covariant hamiltonian dynamics // Physical Review D. — 2007. — Т. 75. — № 2. — С. 025027.
3. Гото М., Гроссханс Ф. Полупростые алгебры Ли. — 1981.

