Автоматическое выравнивание горизонта на фотографиях при помощи метода Хафа
Конференция: XI Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

XI Студенческая международная научно-практическая конференция «Молодежный научный форум»
Автоматическое выравнивание горизонта на фотографиях при помощи метода Хафа
ВВЕДЕНИЕ. Сложно представить себе современный мир без сотовых телефонов, фотоаппаратов, камер и прочих гаджетов, способных запечатлеть самые яркие моменты нашей жизни. Но не всегда полученные снимки нас сразу полностью устраивают, и здесь, в арсенале фотолюбителя целый набор различного рода программ и приложений, направленных на обработку и корректировку фотографий. Одной из «проблем», требующих решения и внимания со стороны человека является выравнивание горизонта на фотографиях. Казалось бы, что сложного в том, чтобы изменить положение горизонтальной оси на снимке? Однако, если изображений много, то хотелось бы ускорить и автоматизировать данный процесс. Именно этой задачей мы и занялись в данной работе. Чтобы автоматическое выравнивание горизонта работало на должном уровне для как можно большего числа фотографий, было принято решение разделить эту задачу на отдельные этапы, а именно:
определение границ изображения и всех прямых линий; вычисление наиболее интенсивной линии;
расчет угла между центром изображения и наиболее интенсивной линией; поворот изображения на рассчитанный уровень;
расчет максимального размера прямоугольника, который был бы вписан в повернутое изображение.
ОПРЕДЕЛЕНИЕ ГРАНИЦ. АЛГОРИТМ КАННИ. Перед началом выравнивания изображения по линии горизонта необходимо найти границы наиболее контрастных переходов цвета. Для их определения было решено применять метод Канни, который также необходим в качестве предобработки для получения точек, которые находятся на кривой в изображении.
Джон Канни (John F.Canny) решил математическую проблему по получению фильтра границ, который стал оптимизированным для любого изображения, локализовал и минимизировал несколько откликов одного и того же края. Более того, Канни ввел понятие Non-Maximum Suppression, которое означает, что граничными пикселями признаются точки, в которых достигается локальный максимум градиента в направлении вектора градиента. Детектор использует фильтр на основе первой производной по Гауссу. Однако, так как детектор восприимчив к шумам, лучше не применять данный метод на необработанном изображении.
Алгоритм состоит из пяти отдельных шагов:
1. Сглаживание. Размытие изображения для удаления шума.
2. Поиск градиентов. Границы отмечаются там, где градиент изображения приобретает максимальное значение.
3. Подавление не-максимумов. Только локальные максимумы отмечаются как границы.
4. Двойная пороговая фильтрация. Потенциальные границы определяются порогами.
5. Трассировка области неоднозначности. Итоговые границы определяются путем подавления всех краев, несвязанных с определенными (сильными) границами.
Оператор Кэнни использует фильтр, который может быть хорошо приближен к первой производной гауссианы. σ {\displaystyle \sigma } σ= 1.4:
|
|
|
|
Рисунок 1. Матрица преобразования |
Рисунок 2. Схема трассировки |
Границы выделяются в тех местах, где градиент исследуемого изображения приобретает наибольшее значение. Они могут иметь разную направленность, поэтому алгоритм Канни использует четыре фильтра: горизонтальные, вертикальные и диагональные ребера в размытом изображении: 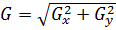 ;
; 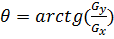 ;
;
Угол наклона вектора градиента округляется и может принимать значения 0, 45, 90, 135. Но границами отмечаются только локальные максимумы. Итоговые границы находятся путём исключения всех краёв, не связанных с определенными границами. Перед применением детектора обычно преобразуют изображение в оттенки серого, чтобы уменьшить вычислительные затраты.
|
|
|
|
|
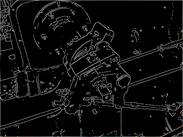
Рисунок 3. Оригинал изображения
|
Рисунок 4. Изображение после применения маски Гаусса 5x5 |
Рисунок 5. Детектор границ Canny
|
Задача преобразования Хафа состоит в решении проблемы группировки граничных точек с помощью применения процедуры голосования к набору параметризованных объектов изображения. В общем случае прямая линия задается уравнением y = kx + b и может быть вычислена по любой паре точек (x, y) на изображении. Главная идея преобразования Хафа заключается в учете характеристик прямой не в виде уравнений, построенных по паре точек изображения, а с помощью параметров, задающих ее, то есть k — коэффициента наклона и b — точки пересечения с осью ординат. Таким образом, прямая, представленная уравнением y = kx + b, может задаваться в виде точки с координатами (b, k) в пространстве параметров.
Поскольку параметр k имеет бесконечные значения для прямых, параллельных к оси ординат, то удобней представить прямую с помощью других параметровθ {\displaystyle \theta } . Положим, параметр r {\displaystyle r} r — это длина радиус-вектора ближайшей к началу координат точки на прямой, аθ {\displaystyle \theta } ϑ — это угол между этим вектором и осью абсцисс. Уравнение прямой после преобразований можно записать в виде: 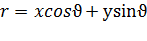 , тем самым, исключая проблему бесконечности параметров. Бесконечно множество прямых линий может пересекать каждую точку плоскости. Если эта точка имеет координаты (
, тем самым, исключая проблему бесконечности параметров. Бесконечно множество прямых линий может пересекать каждую точку плоскости. Если эта точка имеет координаты ( 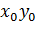 ), то все прямые, проходящие через неё, соответствуют уравнению:
), то все прямые, проходящие через неё, соответствуют уравнению: 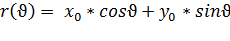 . Это соответствует синусоидальной линии в пространстве Хафа (r,
. Это соответствует синусоидальной линии в пространстве Хафа (r, 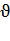 ), которая, в свою очередь, уникальна для данной точки и однозначно её определяет. В случае наложения этих линий, соответствующих двум точкам, друг на друга, точка их пересечения соответствует прямым (в оригинальном месте изображения), проходящим через обе точки. Таким образом, проблема обнаружения коллинеарных точек может быть сведена к проблеме обнаружения пересекающихся кривых.
), которая, в свою очередь, уникальна для данной точки и однозначно её определяет. В случае наложения этих линий, соответствующих двум точкам, друг на друга, точка их пересечения соответствует прямым (в оригинальном месте изображения), проходящим через обе точки. Таким образом, проблема обнаружения коллинеарных точек может быть сведена к проблеме обнаружения пересекающихся кривых.
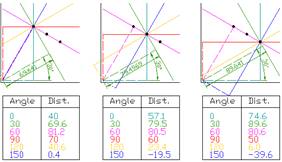
Рисунок 6. Визуализация преобразования Хафа
Далее рассмотрим изображение, сформированное из трех черных точек. Проверим, расположены ли точки на прямой линии и к каждой прямой из начала координат построим нормаль. Для всех прямых длина соответствующей нормали и ее угол с осью абсцисс представлены в таблице. Значения, указанные в таблице, являются результатом преобразования Хафа и могут служить основой для графического представления в "пространстве Хафа". Однако, следует отметить, что выполненное преобразование дает неоправданно большое множество линий. Более того, с помощью него формируется матрица, в которой по горизонтали отсчитываются углы линий, а по вертикали — расстояние от центра до линии, что неудобно для последующих этапов. Для решения этих проблем, была написана функция преобразования линий из полярных координат в прямоугольные:
public static double CalculateAngle(int width, int height, double x1, double y1, double x2, double y2)
{doubledx = x2 - x1;doubledy = y2 - y1;
doublex3 = width /2;doubley3 = height /2;
double r = dx * dx + dy * dy;
double nx = (dx * (x3 * dx - dy * y1) + dy * (dx * y3 + x1 * dy)) / r - x3;
double ny = (dx * (y1 * dx - x1 * dy) + dy * (dx * x3 + dy * y3)) / r - y3;doubleresult = Math.Atan2(ny, nx) + Math.PI /2;
if(result > Math.PI) result = result - Math.PI *2;returnresult; }
Стоит отметить, что если вычисленный угол становится больше определенного заданного значения поворота (в нашем случае это 45°), то автоматический поворот выполняться не будет. После того как расчитан угол, на который нужно повернуть изображение, необходимо вычислить размеры наибольшего прямоугольника, вписанного в повернутое изображение. Стоит отметить, что данный прямоугольник может быть как пропорциональным, так и непропорциональным, покрывающим всю максимальную площадь в повернутом изображении. Чтобы лучше понять работу каждого из этапов, предлагаем вашему вниманию следующий рисунок.

Рисунок 7. Пример работы
ЗАКЛЮЧЕНИЕ В итоге, проведя серию экспериментов по автоматическому выравниванию различных изображений вдоль линии горизонта, нам удалось прийти к достаточно высокому соотношению удачного/неудачного поворота картинки, достигнув при этом высокой скорости работы с объектами. Была устранена и проблема со сглаживанием, из-за которой отредактированные фотографии теряли в качестве. Таким образом, посредством варьирования коэффициентов в алгоритме определения границ и преобразования Хафа, нам удалось создать достаточно гибкий и удобный инструмент для работы с изображениями, который может найти применение в различных областях графической обработки и дизайна.