ЧИСЛА СКЬЮЗА: ТЕОРИЯ И ПРАКТИКА

Число Скьюза (англ. Skewes number) — наименьшее натуральное число n, такое, что, начиная с него, неравенство  перестает выполняться, где π(n) — количество простых чисел, не превосходящих n также называемой функцией распределения простых чисел или пи-функция, а 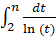  — сдвинутый интегральный логарифм. Джон Литтлвуд в 1914 году привел неконструктивное доказательство того, что такое число существует.

Стэнли Скьюз в 1933 году оценил это число, исходя из гипотезы Римана, как   — первое число Скьюза, обозначающееся Sk₁. Он же в 1955 году  примерно определил, без предположения о верности гипотезы Римана, что 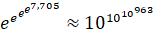  , в дальнейшем названное вторым числом Скьюза, обозначающееся Sk₂. Это одно из самых больших чисел, имеющих свое название, когда-либо применявшихся в математических доказательствах, хотя и намного меньше, чем число Грэма. В 1987 году Герман Риел (H. J. J. te Riele) без учета гипотезы Римана определил, что число Скьюза  приблизительно равно 8,185·10³⁷⁰ (далее в статье оно будет называться Sk₃). К 2017 году было принято считать, что число Скьюза заключено между 10¹⁹ и 1,3971672·10³¹⁶ ≈ e^{727,951336108}.  [1]

Вопрос целостности Sk₁= является открытой математичекой проблемой. [2]

Для нахождения значений трех выше названных чисел, была применена программа, написанная мной (автором статьи) на языке С++, код которой приведен ниже:

#include <iostream>

#include <math.h>

#include <ctype.h>

#include <string>

#include <stdlib.h>

using namespace std;

int main() {

long double const e= 

         long double e1, e2, sk1,n,t,u, e3,sk1w, e4,e5,e6,sk2,k,i,j,r,x;

         long double const c = 27/4;

         string s1, s2, s3;

         e1 = pow(e, e);         //Вычисление Sk1

         e2 = pow(e1, e);

         sk1 = pow(e2, 79);

         s1 = to_string(sk1);    //Вывод Sk1

         cout << "Sk1 = " << s1 << endl;

         n = modf(sk1,&t);

         if (n == 0&&sk1>0) {         //Проверка на целостность Sk1

                   cout << "Sk1 is integer" << endl;

         }

         else {

                   cout << "Sk1 is not integer" << endl;

         }

         e4 = pow(e, e);    //Вычисление Sk2

         e5 = pow(e4, e);

         e6 = pow(e5, e);

         sk2 = pow(e6, 7.705);

         s2 = to_string(sk2);       //Вывод Sk2

         cout << "Sk2 = " << s2 << endl;

         k = modf(sk2, &u);

         if (k == 0 && sk2 > 0) {     //Проверка на целостность Sk2

                   cout << "Sk2 is integer " << endl;

         }

         else {

                   cout << "Sk2 is not integer" << endl;

         }

         e3 = pow(e, e);          //Вычисление Sk3

         sk1w = pow(e3, c);

         j = modf(sk1w, &i);

         s3 = to_string(sk1w);    //Вывод Sk3

         cout << "Sk3 = " << s3 << endl;

         if (j == 0 && sk1w > 0) {       //Проверка на целостность Sk3

                   cout << "Sk3 is integer" << endl;

         }

         else {

                   cout << "Sk3 is not integer" << endl;

         }

         return 0;

}

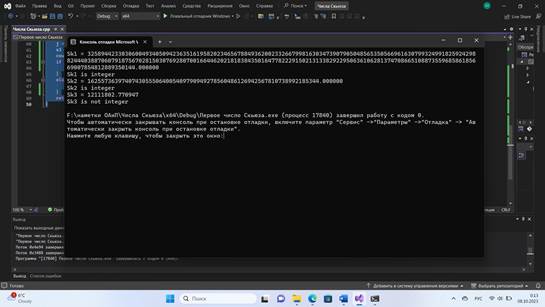
Рисунок. Результаты работы кода

Согласно рисунку Sk₁ и Sk₂ являются целыми числами, а Sk₃ не является целым числом. Но следует учесть, что вычисления с использованием ЭВМ являются приближенными.

Вот их приближенные значения:

Sk₂16255736397407430555064005409790949278560486126942567810738992185344

Sk₃12111802,770947

Однако, если в коде значение переменной «с» изменить с 27/4 на 6,75 (27/4=6,75) то значение Sk₃ будет совсем другим, оно помечено как Sk₃^*:

Sk₃^*93027187,034304

В программе Microsoft Excel версии 2021:

Sk₁ = 3,2589*10²⁵³

Sk₂ = 1,62557*10⁶⁷

 Sk₃ = 93027187,0343043

Программа PTC Mathcad Prime 3.0 вычислить числа не позволяет, т.к. амплитуда чисел превышает значение 10³⁰⁷.

Таким образом мы видим, что использование современных ЭВМ и ПО позволяют выпонить вычисления, ранее невозможные при использовании классических методов.

Сами исследования простых чисел широко используются в теории чисел, современной криптографии и криптологии.