Исследование масштабируемых алгоритмов анализа графов на основе фреймворка Apache Flink

С каждым днем размеры графов увеличиваются, их сложность растет, и даже такая важная задача, как визуализация, становится проблематичной. Один из возможных подходов к ее решению заключается в более высокоуровневом представлении исходного графа. Однако, важно, чтобы при группировке вершин не потерялась глобальная структура графа. Такие группы можно назвать сообществами в графе.

Методы выделения сообществ в социальных графах активно исследуется в последнее время, и визуализация графа всего лишь один из практических аспектов этой задачи. В данной работе анализ графов будет идти именно с этой точки зрения.

На концептуальном уровне сообществом называется такая группа вершин, что внутригрупповые связи гораздо плотнее межгрупповых, что хорошо видно на рис. 1.

Обычно также делают предположение, что сообщество состоит из одной компоненты связности. В противном случае его можно разделить на несколько более мелких сообществ.

В этой работе будет использоваться такое предположение о структуре сообществ в графе, согласно которому каждая вершина графа входит в одно и только одно сообщество.

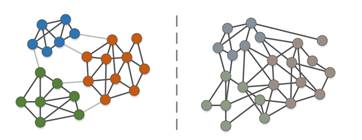
Рисунок 1. Пример графа, который имеет структуру из трех сообществ (слева) и графа на тех же вершинах, который ее не имеет (справа)

Из предположения сразу следует, что сообщества полностью покрывают граф. Тогда можно говорить о поиске сообществ в графе как о задаче поиска разбиения множества вершин на подмножества, которое минимизирует некоторый функционал.

Исследование проводилось на программном комплексе Apache Flink. Apache Flink является распределенной платформой обработки данных для использования данных в больших приложениях, прежде всего, включая анализ данных, хранящихся в кластерах Hadoop. Поддерживает комбинацию обработки в оперативной памяти и на основе диска.

В качестве алгоритмов исследования были выбраны два наиболее популярных алгоритма: Community Detection и Connected Components.

Рассмотрим алгоритм Community Detection подробнее. Обнаружение структуры сообщества в сети как правило, предназначено для процедуры отображения сети в дерево, известной как дендрограмма. В этом дереве, листья - это узлы и ветви соединяют их или (на более высоком уровне) группу листьев, тем самым идентифицируя иерархию сообществ. Узлы могут быть либо агломерированы последовательно начиная от отдельных узлов (агломератов), или вся сеть может быть рекурсивно разделенной.

Ньюмен и Гирван представили алгоритм семантического деления, в котором выбор удаляемого ребра основан на значении наибольшей промежуточности, количество кратчайших путей между всеми парами узлов проходящих через этот узел. Ясно, что когда граф состоит из тесно связанных кластеров, каждый из которых взаимосвязан, все кратчайшие пути между узлами в разных кластерах проходят через несколько межкластерных ребёр, которые поэтому имеют большое значение промежуточности. Рекурсивное удаление этих рёбер с большой промежуточностью делит сеть в сообщества разных размеров.

В данной работе был использован модифицированный алгоритм Ньюмана-Гирвана с использованием дополнительного параметра затухания переходов (Hop attenuation).

Используется оценка, которая привязана к каждой метке, и уменьшается по мере того как проходит через источник. При инициализации, каждый узел получает оценку 1.0 для своей метки. После того как узел  собрал со всех окружающих его узлов  все метки и оценки для них, происходит вычисление новой метки и соответствующей оценки.

В общем виде вычисление новой метки может быть представлено как:

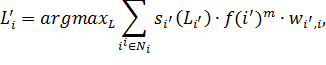
где  метка узла ,  оценка хопа метки  в узле ,  вес ребра между узлами  и ,  произвольная сопоставимая характеристика для каждого узла . Например, если определить , когда , предпочтение отдается узлу с большим количеством соседей, когда  – с меньшим. Последний шаг, назначение новой метки и соответствующей ей оценки в узел , вычитая из оценки параметр затухания переходов :

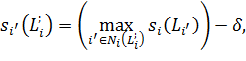
где  набор соседей узла , которые имеют метку .

Алгоритм прекращает свое действие, когда ни один узел не меняет свое значение или достигнуто максимальное число итераций, введённое пользователем.

Теперь рассмотрим алгоритм Connected Components.

Алгоритм реализуется с использованием итераций scatter-gather. Эта реализация использует сопоставимое значение вершин в качестве идентификатора начального компонента (ID).

Вершины распространяют свое текущее значение на каждой итерации. После получения идентификаторов компонентов от своих соседей вершина принимает новый идентификатор компонента, если его значение меньше его текущего идентификатора компонента.

Алгоритм сходится, когда вершины больше не обновляют свое значение идентификатора компонента или, когда достигнуто максимальное количество итераций.

Для исследования был взят набор данных, состоящий из 1005 узлов и 25571 рёбер. Набор данных был создан с использованием данных электронной почты из большого европейского исследовательского учреждения. В нём содержится анонимная информация обо всех входящих и исходящих сообщениях электронной почты между членами исследовательского учреждения. В сети есть ребро (u, v), если человек отправил человеку по крайней мере одно электронное письмо. Электронные письма представляют только связь между членами организации, а набор данных не содержит входящие сообщения или исходящие сообщения.

Идеальное распределение на группы, заданное в начальном наборе данных представлено на рисунке 2.

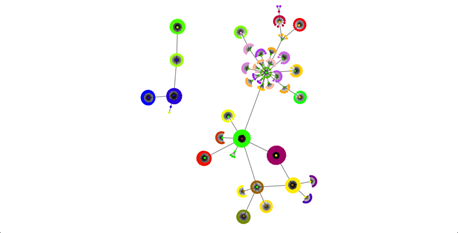
Рисунок 2. Идеальное распределение на сообщества

Рассмотрим работу обоих алгоритмов на заданном наборе данных. Результат работы двух алгоритмов представлен на рисунке 3.

Рисунок 3. Результат работы двух алгоритмов, слева Community Detection, справа Connected Components

Было выявлено по меньшей мере 25 крупных групп. Этот граф отдаленно напоминает идеальный граф и результат работы обоих алгоритмов схожи.

При схожем времени работы и затрачиваемых ресурсах, алгоритм Community Detection даёт более точные результаты, и при увеличении количества итераций имеет меньшую тенденцию к выделению больших сообществ, не несущих в себе почти никакой информации.

В первую очередь это связано с более комплексным подходом алгоритма к сравнению вершин и решении об определении какой-либо вершины в группу. В то время как Connected Components заключает в себе более простую и просто реализуемую логику работы, с чем и связана его большая погрешность и некоторая неточность в результатах.