МОДЕЛИ ОДНОМЕРНЫХ ДИСПЕРСИОННЫХ ВОЛН В ТВЕРДЫХ ТЕЛАХ С МИКРОСТРУКТУРОЙ

Аннотация. Каждый материал обладает микроструктурой определенного масштаба. Микроструктура может быть правильной или хаотичной, естественной или искусственной. Общей чертой любой микроструктуры является то, что ее характерный масштаб намного меньше размера рассматриваемого объекта. В классической механике сплошной среды не учитывается существование микроструктуры. Очевидно, что классическое волновое уравнение необходимо модифицировать, чтобы включить наблюдаемые дисперсионные эффекты, обусловленные микроструктурой. Ниже мы рассмотрим возможные модификации волнового уравнения в простом одномерном случае.

Классическое уравнение распространения линейной упругой волны в однородных твердых телах в одномерном случае

                                                           (1)

имеет решение в виде гармонической волны

                                                        (2)

где u - перемещение, c - скорость упругой волны, нижние индексы обозначают производные,  - амплитуда, k - волновое число и ω – частота.

Подставляя гармоническое волновое решение (2) в волновое уравнение (1), приходим к дисперсионному соотношению

                                                           (3)

Гармонические волны характеризуются фазовой скоростью c_p и групповой c_g

                                                                  (4)

Согласно уравнению (3), групповая скорость равна фазовой скорости в случае однородной среды. Соответствующая дисперсионная кривая представлена прямой линией (Рис. 1). Гармонические волны в однородной среде сохраняют форму и скорость, что означает отсутствие дисперсии. Для описания распространения волн в неоднородных материалах, отражающих эффекты дисперсии, было предложено несколько модификаций волнового уравнения.

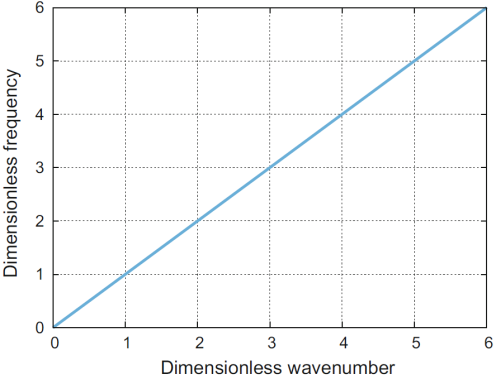
Рисунок 1. Дисперсионная кривая для волнового уравнения (1)

Простейшим обобщением волнового уравнения является модель градиента деформации. Модель градиента деформации [12] предполагает, что плотность свободной энергии зависит не только от деформации, но и от ее градиента. Соответствующее уравнение движения [12]

                                                      (5)

дисперсионное соотношение

                                                         (6)

Введение безразмерной частоты и волнового числа

                                                          (7)

где ω₀ - характерная частота, и используя безразмерный параметр b, определяемый формулой

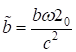                                                             (8)

можно переписать дисперсионное соотношение (6) в безразмерном виде

                                                      (9)

Это дисперсионное соотношение проиллюстрировано на рис. 2 для .

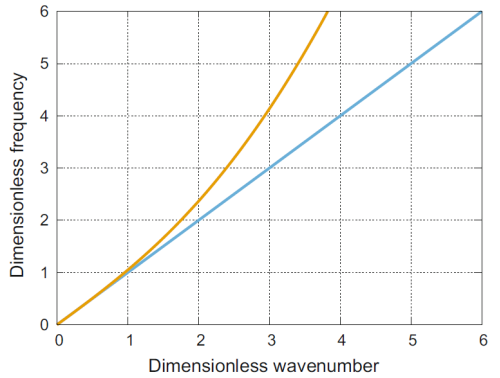
Рисунок 2. Дисперсионные кривые: синяя линия соответствует волновому уравнению (1), светло-коричневая - модели градиента деформации.

Соответствующая дисперсионная кривая является выпуклой и расположена над прямой, характеризующей классическое волновое уравнение. В то же время экспериментальные наблюдения показывают, что дисперсионные кривые для твердых тел должны быть вогнутыми и располагаться ниже этой прямой [2, 7]. Более того, реальные материалы демонстрируют оптическую ветвь кривой дисперсии [3]. Это означает, что описание эффектов дисперсии в микроструктурированных твердых телах - нетривиальная задача и определенно не может быть получена в рамках простой модели градиента деформации.

Простейшая попытка улучшить описание волновой дисперсии в твердых телах приводит к линейной версии уравнения Буссинеска для упругих кристаллов

                                        (10)

где l - параметр внутренней длины, а A11> 0 - безразмерный коэффициент. То же уравнение было получено с помощью гомогенизации периодически слоистой среды [15], гомогенизации более высокого порядка с множеством пространственных и временных масштабов [6], а также с помощью процедуры континуализации для дискретной цепочки пружина-масса [11]. Дисперсионное соотношение можно представить в безразмерном виде

                                                   (11)

Пример соответствующей дисперсионной кривой показан на рис. 3 для значения безразмерного параметра γ= 0,41.

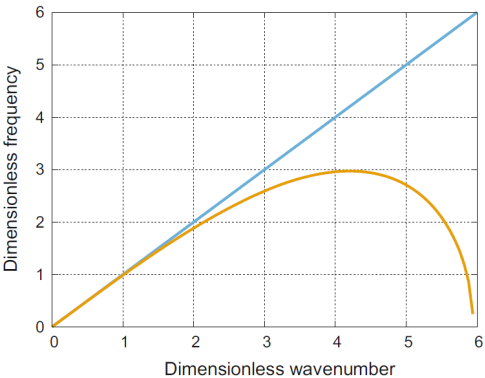
Рисунок 3 Дисперсионные кривые: синяя линия соответствует волновому уравнению (1), светло-коричневая линия - уравнению типа Буссинеска (10) для γ = 0,41

Другим обобщением волнового уравнения является уравнение Лява-Рэлея для стержней, учитывающее инерцию [8]

                                           (12)

Безразмерный вариант дисперсионного соотношения записывается

                                                (13)

Кривая дисперсии выглядит более подходящей, как это видно на рис. 4, но она демонстрирует горизонтальный асимптотический предел, что означает, что все частоты выше определенного значения запрещены.

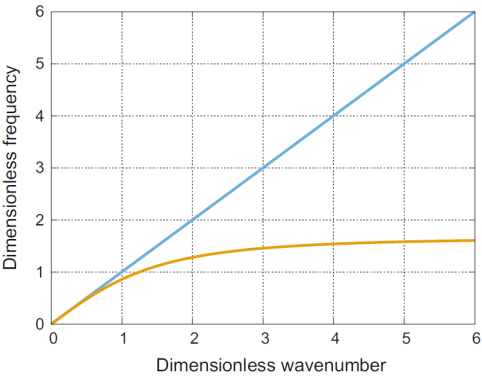
Рисунок 4. Дисперсионные кривые: синяя линия соответствует волновому уравнению (1), светло-коричневая - уравнению типа Лява-Рэлея (12) для γ1 = 0,6

Более общее уравнение, объединяющее две упомянутые выше модели дисперсии, было разработано путем континуализации модели пружины и массы [11]

                                 (14)

Такое же дисперсионное волновое уравнение выводится на основе объединения локальной и нелокальной деформации в определяющем упругом соотношении [5] и следует из теории микроструктуры Миндлина [13, 14]. Более точная модель типа Миндлина [4, 5] вводит дополнительно вклад микроструктуры в замедление скорости распространения c_A

                      (15)

Безразмерный вариант дисперсионного соотношения записывается

                         (29)

Это показано на рис. 5.

Рисунок 5. Дисперсионные кривые: синяя линия соответствует волновому уравнению (1), светло-коричневая - модели Миндлина (14) для γ’ = 0,6, γA = 0,4, γ = 0,3

Благодаря объединению трех дополнительных членов последняя модель дисперсии волн является более гибкой, но по-прежнему имеет только акустическую ветвь дисперсионной кривой.

Производная четвертого порядка по времени вводится в рассмотрение моделью аномальной дисперсии Максвелла-Рэлея [9]

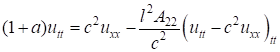                                       (16)

Кривая дисперсии имеет как оптическую, так и акустическую ветви, как это показано на рис. 6. Однако акустическая ветвь снова асимптотически ограничена.

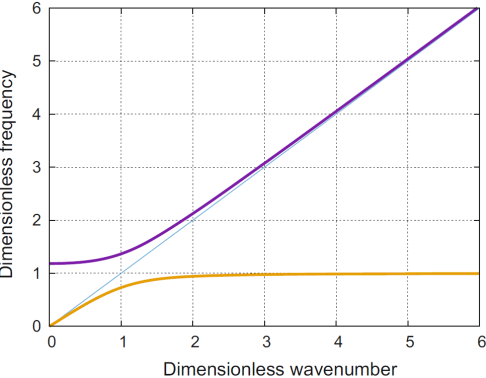
Рисунок 6. Дисперсионные кривые: темно-фиолетовая линия соответствует оптической ветви, светло-коричневая - акустической ветви модели аномальной дисперсии Максвелла-Рэлея с a = 0,4, γ2 = 1

Производная четвертого порядка по времени также включена в феноменологическую «причинную» модель распространения дисперсионных волн, предложенную в [10]

                         (17)

и в модели, основанной на теории микроструктуры Миндлина [5]

                             (18)

Здесь p и c₁ определяют масштабы времени и длины микроструктуры, соответственно, c₁ может быть связано со скоростью распространения волны в самой микроструктуре.

Явное выражение для замедления скорости распространения является преимуществом последней модели. Поучительно сравнить дисперсионные свойства двух последних моделей. Соответствующие дисперсионные соотношения можно представить в виде

                                   (19)

                                  (20)

Дисперсионные кривые для обеих моделей имеют как акустическую, так и оптическую ветви (рис. 7 и 8), но дисперсионные кривые для так называемой «причинной» модели [10] отклоняются от асимптот с увеличением параметра γ

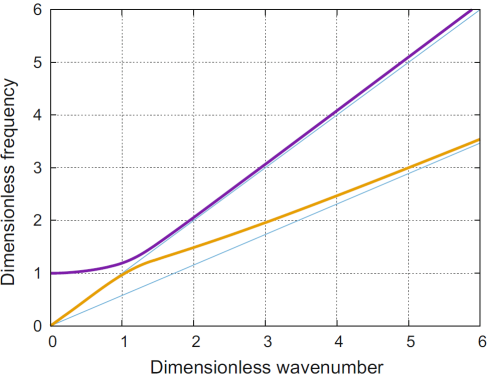
Рисунок 7. Дисперсионные кривые: темно-фиолетовая линия соответствует оптической ветви, светло-коричневая - акустической ветви причинной модели (17) для γ1 = 0,6, γ = 0,4, γ2 = 1 (цветной рисунок онлайн)

Рисунок 8. Дисперсионные кривые: темно-фиолетовая линия соответствует оптической ветви, светло-коричневая - акустической ветви модели типа Миндлина (18) для γ1 = 0.6, γA = 0.4. Синие линии представляют собой асимптоты дисперсионных кривых

Все перечисленные выше модели основаны либо на усреднении, либо на континуализации, либо на обобщенных теориях континуума. Методы асимптотической гомогенизации не обеспечивают высших производных по времени, поэтому соответствующие модели не включают оптическую ветвь дисперсионной кривой, что критически важно для учета микроструктурных эффектов.

Наиболее многообещающий подход основан на обобщенных теориях континуума [14].

В этом направлении модель типа Миндлина [5] дает наиболее общее дисперсионное волновое уравнение. Конечно, есть возможность строить модели, состоящие и из более высоких производных, однако это похоже на игру с производными высших порядков, игнорирующую задачу с начальными и граничными условиями