ПРИМЕНЕНИЕ РАСПРЕДЕЛЕНИЯ «ХИ-КВАДРАТ» ДЛЯ СТАТИСТИЧЕСКОГО АНАЛИЗА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ

Распределение «Хи-квадрат» является одним из основных методов в статистике и используется для проверки различных статистических гипотез.

Критерий согласия применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению.

Его расчетная формула выглядит таким образом:

,

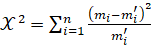где m—эмпирические частоты, m’– теоретические частоты;

n — число степеней свободы.

Для проверки гипотезы нам необходимо сравнить эмпирические (реальные) и теоретические частоты.

Распределение вероятных значений случайной величины χ² непрерывно и ассиметрично. Оно зависит от числа степеней свободы (n) и приближается к нормальному распределению по мере увеличения числа наблюдений. Поэтому применение критерия χ² к оценке дискретных распределений сопряжено с некоторыми погрешностями, которые сказываются на его величине, особенно на малочисленных выборках [1, c.23].

Точность определения критерия χ² в значительной степени зависит от точности расчета теоретических частот (m’ i ), для получения разности между эмпирическими и вычисленными частотами следует использовать неокругленные теоретические частоты.

Частота - это количество возникновений какого-либо события. Частоту появления события обычно имеют в виду, когда переменные измеряются в номинальной шкале и другие их характеристики, кроме частоты возникновения, невозможно или трудно подобрать. Другими словами, когда переменная имеет качественные характеристики.

Рассмотрим применение критерия «Хи-квадрат» на примере полученных результатов испытаний ЭКБ.

Очевидно, что изделий надлежащего качества больше, однако, это нужно доказать статистически. Для этого используем критерий «хи-квадрат».

Результаты испытаний были распределены на три группы: годен, сомнительный результат (требуются дополнительные испытания), не годен.

Частоты выглядят следующим образом:

Годен (Г) — 87 шт.

Сомнительный результат (С) — 8 шт.

Не годен (Н) — 5 шт.

Требуется проверить, отличаются ли полученные эмпирические данные от теоретических. Для этого необходимо найти теоретические частоты. В нашем случае теоретические частоты – это равновероятные частоты, которые находятся путем сложения всех частот и деления на количество групп.

В нашем случае:

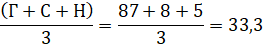
Построим сравнительную таблицу.

Таблица.

Результаты испытаний

Далее найдем сумму последнего столбца: χ² = 129,9. Теперь нужно найти критическое значение критерия. Для этого используем число степеней свободы (n) и таблицу распределения χ² .

Число степеней свободы рассчитывается по следующей формуле:

,

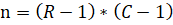где R – количество строк в таблице, C – количество столбцов.

В нашем случае учитывается только один столбец и три строки, поэтому формула изменяется:

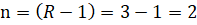
Для вероятности ошибки p≤0,05 (принятой в статистических исследованиях) и n = 2 критическое значение χ² = 5,99. Полученное эмпирическое значение больше критического – различия частот достоверны (χ² = 129,9; p≤0,05). Следовательно, гипотеза о том, что расхождение между эмпирическими и теоретическими (ожидаемыми) частотами носит случайный характер, опровергается. Метод расчета критерия «Хи-квадрат» является простым и быстрым, демонстрируя значительную практическую пользу. Этот критерий имеет большую ценность при анализе результатов испытаний ЭКБ, играя важную роль в процессе исследования.