МЕТОДЫ АНАЛИЗА ДАННЫХ СЕТЕВОЙ АКТИВНОСТИ АБОНЕНТОВ

Существует достаточно много подходов к анализу данных сетевой активности абонентов. В конечном итоге, именно цель анализа определяет выбор того или иного метода. Поэтому в таблице 1 представим методы и тезисное описание того, какие проблемы анализа данных позволяют решить эти методы:

Таблица 1.

Направления и методы анализа данных

Рассмотрим представленные в таблице 1 методы более подробно.

Пусть у нас есть определенный массив факторов Хi, которые, как уже было отмечено выше, являются клиентскими и техническими метриками сетевой активности. Y – это результирующая переменная, которая показывает конечную эффективность для пользователей. Например, многие компании используют в качестве Y показатель NPS – удовлетворенность клиентов от оказанных услуг, вероятность того, что они порекомендуют услуги компании другим абонентам.

Математически, связь между факторами и результирующей переменной, находится посредством корреляционно-регрессионного анализа. Главное преимущество регрессии состоит в том, что в модели могут быть рассмотрены факторы, имеющие разную размерность, кроме того, это могут быть количественные и качественные переменные. Общее уравнение, при помощи которого описывается регрессия, представлено в (1.1):

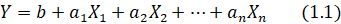
В качестве Х берутся данные, представленные либо за определенную единицу времени, либо соответствующие определенному состоянию среды. Решение задачи связи Х и У лежит в разрезе двух методов – метод наибольшего правдоподобия и метод наименьших квадратов, при этом, метод наименьших квадратов является более простым и интерпретируемым - формула (1.2):

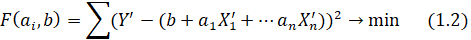
Нахождение коэффициентов множественной регрессии методом наименьших квадратов при больших данных – сложная задача. Существует достаточно много программных средств для решения задачи регрессии. Отметим наиболее распространенные:

- коэффициенты регрессии возможно получить при помощи функции ЛИНЕЙН в Excel, при этом формируется массив 2*5 с коэффициентами регрессии и параметрами регрессионной модели, в частности, коэффициентом детерминации;

- надстройка «Регрессия» - более продвинутый способ, который позволяет также оценить и другие параметры регрессионной модели, характеризующей ее точность и качество;

- однако, Excel достаточно проблемно работает с данными размером более 1 млн. строк. Поэтому библиотеки распространенных языков программирования, например, Python, также реализуют встроенные методы. Например, такой библиотекой является sklearn – пакет для продвинутой аналитики, реализующий не только линейную, но и нелинейные регрессии.

Итак, линейная модель – это частный случай модели регрессии. [1] Как правило, линейную модель используют достаточно часто, поскольку с бизнесовой точки зрения она интерпретируется проще всего. В то же время, когда речь идет о специфичных зависимостях, например с выраженной сезонностью, использовать линейную модель проблематично ввиду низкого уровня аппроксимации. Поэтому также необходимо рассматривать и другие нелинейные модели. Остановимся более подробно на основных моделях, которые будут использоваться в практической части работы:

- модель сезонности, крайне распространенная при анализе сетевой активности – это связано с началом и окончанием учебного года, сезоном отпусков и т.п. Для сезонных моделей как правило используются гармонические регрессии, ряды Фурье и т.п.;

- полиномиальная модель, например параболическая, с выраженными восходящей и нисходящей компонентой в форме колокола;

- логарифмическая модель – когда речь идет о зависимости с нарастающим итогом, которая, как правило, подчиняется закону Парето 80 на 20.

Важным инструментом эконометрического анализа является корреляционный анализ, который позволяет существенно продвинуться в контексте определения взаимосвязей между переменными. Суть корреляционного анализа заключается в нахождении коэффициентов корреляции – именно они позволяют интерпретировать через числовую форму тесноту связи между факторами и результирующей переменной, а также между факторами друг с другом. Коэффициент корреляции всегда лежит на отрезке от -1 до 1. Значения меньше 0 характеризуют обратную связь, значения больше 0 – прямую. Существует достаточно много шкал интерпретации коэффициентов корреляции, наиболее распространенной является шкала Чеддока. В любом случае, для каждого конкретного случая необходимо интерпретировать коэффициенты корреляции в соответствие не только с определенной шкалой, но и со здравым смыслом. В контексте корреляционно-регрессионного анализа возникает проблема мультиколлинеарности. Эта проблема существенно снижает точность модели регрессии. Сущность проблемы заключается в том, что факторы, которые входят в модель, могут тесно коррелировать друг с другом, поэтому оставлять мультиколлинеарные факторы не имеет смысла. Как правило, при коэффициентах корреляции больше 0,7 по модулю факторы считаются коррелирующими друг с другом, поэтому в модели оставляют какой-либо один из этих факторов. После построения модели регрессии происходит определение качества уравнения при помощи следующих критериев:

- коэффициент детерминации, который в частном случае линейной однофакторной модели равен квадрату коэффициента корреляции между Х и У. Как правило, приемлемым коэффициентом детерминации считается значение от 0,8, но, как уже было отмечено выше, возможны допущения, например, при невозможности построения более качественного уравнения регрессии или его сложной интерпретируемости;

- коэффициенты t-критерия, характеризующие случайность каждого члена в уравнении регрессии. При незначимых по t-критерию переменных, они удаляются из модели регрессии;

- F-критерий Фишера, характеризующий общее качество уравнения регрессии;

- стандартная ошибка аппроксимации, показывающая, на какой средний процент отклоняется прогнозное значение уравнения регрессии от фактического. Приемлемое значение составляет 8%, в различных ситуациях допускается уровень от 10 до 15%.

Перейдем к кластерному анализу, который применяется практически во всех сферах анализа данных. Основная сущность кластерного анализа – это своего рода группировка похожих пользователей и их дальнейшее исследование уже в рамках этого кластера (группы). Основным математическим методом кластеризации является метод k-means (k-средних), который предусматривает следующие этапы. Пусть в качестве метрики у нас будет медианное время сессии абонента за прошедший месяц.

1) Выбираем число кластеров k, например, это может быть сделано с помощью визуального анализа, а также при помощи статистических группировок (к примеру, по персентилям);

2) В зависимости от выбранного числа кластеров, выбираем k-случайных значений, которые будут использоваться как центроиды для каждого кластера;

3) Определяем расстояние от фактического значения до центроида – это позволяет нам определить, к какому кластеру принадлежит тот или иной абонент в зависимости от его медианного времени сессии;

4) Пересчитываем центроиды для каждого k-кластера, используя формулу расстояния между точками;

5) Оцениваем качество кластеризации с использование метрики WCSS (within-cluster sum of squares) – cумму квадратов внутрикластерных расстояний до центра кластера.

Большинство методов оперативного исследования, которые рассмотрены выше, в основном связаны с очень конкретной контентной задачей. Так, определение взаимосвязей между переменными с использованием корреляционного анализа – это получение классической матрицы корреляции, на основании которой уже можно принимать управленческие решения. В некоторых ситуациях факторы, характеризующие сетевую активность, достаточно вариабельны и их статическое рассмотрение на небольших временных отрезках не дает нужной математической точности. Решением являются модели динамического программирования. Таким образом, рассмотренные методы позволяют, в целом, достигнуть основной цели анализа данных сетевой активности абонентов, а именно реализовать функцию связи аналитики и бизнеса.