Усилия в покрытиях с радиальной системой вант

При расчетах висячих покрытий полагают, что вертикальная нагрузка воспринимается одними вантами, работающими подобно гибким нитям лишь на растяжение. Кровельное ограждение считается либо полностью пассивным, либо способным воспринимать одни сжимающие усилия [1]. Лишь в отдельных случаях в зависимости от материала и конструктивного решения стыковых соединений сборных элементов кровельное ограждение может воспринимать касательные усилия.

Для многих расчетных случаев ванты могут считаться нерастяжимым и абсолютно гибкими (не обладающими жесткость на изгиб) нитями. Обычно расчет с этими предпосылками дает несколько преувеличенные значения усилий в вантах, что идет в запас прочности [2].

При весьма пологих покрытиях должны приниматься во внимание упругие деформации вантовых систем.

Рассмотрим усилия, возникающие под воздействием вертикальной нагрузки в отдельной гибкой, недеформируемой, свободно висящей нити, закрепленной на опорах, расположенных на одном уровне (рис.1а). Напряжения в ней определяются лишь осевым усилием. Очевидно, реактивные опорные усилия R_A и R_В направлены по касательным к оси нити на ее концах.

Горизонтальные проекции Н_А и Н_В (называемые натяжением нити) соответствующих реактивных усилий могут быть определены из условия: сумма проекций на горизонтальную ось всех сил (в том числе нагрузок), которые на нее действуют, равна нулю. Учитывая, что нагрузка вертикальна, находим: Н_А = Н_В

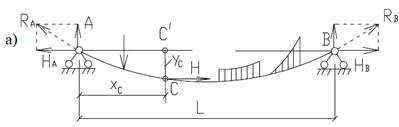
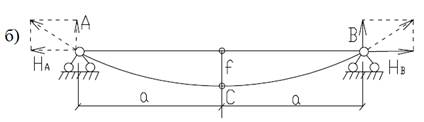
Рисунок 1 Расчетная схема нити (а - нагрузка любого вида; б - нагрузка, равномерно распределенная по длине пролета)

Вертикальные составляющие А и В реактивных опорных усилий R_A и R_B находим из условия равенства нулю моментов заданных сил (нагрузки) и реактивных  сил, действующих на нить, принимая поочередно за моментные точки опоры А и В: 

Для любой точки С, взятой на нити, при моментальной точке  на направлении усилий натяжения существует зависимость

где Н - натяжение нити (горизонтальная проекция усилия в нити) в точке на расстоянии хо от опоры; ус- стрела провисания нити в рассматриваемой точке; Мсб - балочный момент на расстоянии хс от опоры.

Из этого выражения следует, что натяжение троса равно:

.

При нагрузке q, равномерно распределенной по пролету (рис.1а), вертикальные составляющие реакций A =B = ql/2, а наибольший момент  =ql/8.

Полагая, что стрела провисания нити у_c=f_c, находим натяжение ее по выражению:

Где .

Значение продольных усилий N в гибкой нити определяется по формуле:

Где Q_б - поперечная сила, соответствующая балки-проекции.

Как видим, для данного случая задача решается весьма просто. При несимметричной нагрузке провисание нити неизвестно, поскольку оно за висит от вида нагрузки и ее расположения в пролете. Задача также усложняется, если нить подвешена на опорах, находящихся на разных уровнях.

Линия провисания гибкой нити под действием вертикальной нагрузки

q = q(x) определяется ординатой у_с [3]. Она совпадает по очертанию с уменьшенной в Н раз эпюрой моментов в соответствующей шарнирно-опертой балке с пролетом, равным горизонтальной проекции нити, находящейся под действием той же нагрузки: .

При этом тангенс угла наклона нити к горизонту совпадает с уменьшенной в Н раз эпюрой поперечных сил той же балки, а именно

Если известна величина натяжения (распора) Н, то линия провисания может быть определена как  . Если известна хотя бы одна из промежуточных ординат , то известен и распор нити.

Для нерастяжимой нити длиной S справедлива зависимость

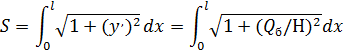
В случае пологой нити

Полагая при этом значение Н постоянным во всем пролете, находим

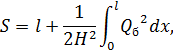
откуда

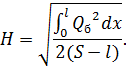
Вычисление интеграла под знаком радикала затруднений не вызывает при любой, в том числе и несимметричной, нагрузке в пролете. При равномерно распределенной нагрузке

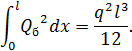
Стрела провисания в середине пролета:

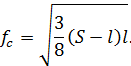
Зависимости для отдельной нити используются при расчете вантовых систем.

Рассмотрим расчет радиальной системы вант в покрытии и с круглым планом при на грузке, равномерно распределенной относительно проекции покрытия.

Поскольку конструкция и нагрузка осесимметричны, каждая нить системы может быть рассчитана самостоятельно.

На рис. 2а в плане выделена одна нить с заштрихованной грузовой площадью, которая ей соответствует, а на рис. 2б показана расчетная схема этой нити. Нагрузка вдоль нити изменяется линейно от нуля в середине до интенсивности q_o= qb, где b - расстояние между тросами по периметру покрытия.

На основании рис. 2б вертикальные и горизонтальные составляющие опорных реакций 

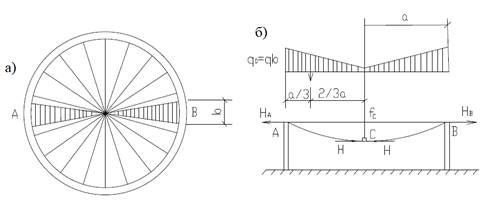
Рисунок 2. К расчету висячего покрытия с радиальной системой вант (а – план; б - расчетная схема троса)

Балочный момент для середины пролета:

а натяжение ванты:

Усилие в ванте

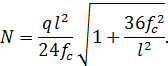
От вант на опорное кольцо передаются радиальные усилия, направленные внутрь области покрытия, интенсивностью

Сжимающее усилие в контурном кольце