СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВЕРОЯТНОСТИ ВЫИГРЫША В СОРЕВНОВАТЕЛЬНЫХ СИСТЕМАХ: ПРИМЕНЕНИЕ ТЕОРИИ ВЕРОЯТНОСТИ К АНАЛИЗУ СТРАТЕГИЧЕСКИХ ИГР И РЕЙТИНГОВЫХ СИСТЕМ

STATISTICAL MODELING OF THE PROBABILITY OF WINNING IN COMPETITIVE SYSTEMS: THE APPLICATION OF PROBABILITY THEORY TO THE ANALYSIS OF STRATEGY GAMES AND RATING SYSTEMS

Maslovsky Pavel Aleksandrovich

Student, Belarusian State University of Informatics and Radioelectronics, Republic of Belarus, Minsk

Kudelko Evgeniy Sergeevich

Student, Belarusian State University of Informatics and Radioelectronics, Republic of Belarus, Minsk

Fedosyuk Lyudmila Petrovna

Scientific supervisor,  Senior lecturer at the Department of Economics Computer Science, Belarusian State University of Informatics and Radioelectronics, Republic of Belarus, Minsk

Аннотация. В статье рассматривается применение теории вероятностей и статистического моделирования к анализу стратегических игр. Рассмотрены примеры из покера, шахмат и Dota 2. Показано, как вероятностные модели и рейтинговые системы позволяют оценивать вероятность выигрыша и прогнозировать результаты соревнований. Также приведено сравнение рейтинговых моделей Эло, Glicko и TrueSkill и показано, как они используются для прогнозирования исходов матчей.

Abstract. The article discusses the application of probability theory and statistical modeling to the analysis of strategic games. Examples from poker, chess and Dota 2 are considered. It shows how probabilistic models and rating systems make it possible to estimate the probability of winning and predict the results of competitions. It also provides a comparison of Elo, Glicko, and TrueSkill rating models and shows how they are used to predict match outcomes.

Ключевые слова: вероятность, статистика, стратегические игры, покер, шахматы, Dota 2, рейтинговые системы.

Keywords: probability, statistics, strategy games, poker, chess, Dota 2, rating systems.

В современных соревновательных системах – от классических игр до киберспорта – оценка шансов на победу имеет решающее значение. Теория вероятностей и математическая статистика предлагают инструменты для моделирования вероятности выигрыша, позволяя анализировать стратегические ситуации и эффективность игроков. Под статистическим моделированием вероятности выигрыша понимается использование случайных моделей или статистических данных для оценки шанса победы одной стороны над другой в условиях неопределенности или неполной информации. Такие подходы получили широкое распространение в спортивной аналитике. В последние годы аналогичные методы начали применяться и к киберспортивным дисциплинам и другим стратегическим играм, где исход зависит как от навыка, так и от элемента случайности.

В данной работе рассмотрены подходы к моделированию вероятности выигрыша на примере трех различных типов игр: покер, шахматы и командная компьютерная игра Dota 2. Особое внимание уделяется рейтинговым системам (таким как система Эло и ее современные обобщения), которые позволяют на основе статистики игр предсказывать вероятности исходов. Приводятся методы имитационного моделирования (Монте-Карло) и аналитические модели, демонстрирующие применение теории вероятностей в анализе данных игр. Цель статьи – показать, как математические модели помогают количественно оценить шансы на победу и сравнить стратегии в разных соревновательных системах.

Покер представляет собой игру, в которой исход отдельной партии сильно зависит от случайного расклада карт, хотя в долгосрочной перспективе навык игрока оказывает значимое влияние. Для оценки шансов выигрыша в покере широко применяется метод статистического (имитационного) моделирования Монте-Карло. Суть подхода заключается в том, что вместо точного аналитического вычисления вероятностей исхода (что часто затруднительно из-за огромного числа возможных раскладов карт) проводится многократное случайное моделирование раздач. Например, для данной ситуации (известны некоторые карты на руках и на столе) генерируются тысячи случайных завершений раздачи и подсчитывается, в скольких из них целевая рука победила. Отношение числа побед к общему числу симуляций дает приближенную вероятность выигрыша рассматриваемой руки. Такой метод позволяет учесть все возможные варианты скрытых карт оппонентов и дальнейших общих карт, не прибегая к сложному перебору всех комбинаций.

Важно отметить, что математически точное вычисление вероятностей в покере возможно для некоторых простых ситуаций (например, вероятность получить определённую комбинацию или улучшить руку с заданным числом аутов). Однако в общем случае, когда на руках у нескольких игроков разные стартовые карты и впереди несколько раундов торговли и открытия карт, аналитическое вычисление становится крайне сложным. Здесь на помощь и приходит моделирование Монте-Карло, позволяющее статистически оценить эквити – долю банков, которую данная рука выиграет в среднем против заданного диапазона оппонента. Специализированные покерные калькуляторы используют подобные алгоритмы, перебирая миллионы случайных раздач для вычисления шансов одной руки против другой или против диапазона рук оппонента.

В играх с полной информацией и отсутствием случайных элементов, таких как шахматы, исход партии в основном определяется сравнительной силой игроков. Теория вероятностей применяется здесь через рейтинговые системы, главной из которых является система Эло. Рейтинг Эло каждого игрока – это численная оценка его способности побеждать других, вычисляемая на основании результатов прошлых партий. Ключевым допущением модели Эло является то, что разность рейтингов двух игроков может быть преобразована в вероятность победы одного над другим. Классическая формула Эло задаёт ожидаемую вероятность выигрыша игрока A против игрока B через разность их рейтингов:

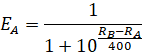
Если рейтинги равны, то вероятность победы каждого игрока равна 50%. Превосходство в рейтинге на определённое число пунктов увеличивает вероятность победы: так, разница ~200 пунктов соответствует тому, что более сильный игрок побеждает примерно в 76% партий, а разница ~400 пунктов – около 91%.

Система Эло оказалась настолько успешной, что её принципы были адаптированы для других игр и соревнований. Например, рейтинговая система Glicko вводит параметр дисперсии, отражающий степень неопределенности рейтинга, а система TrueSkill, применяемая в онлайн-играх, использует байесовский подход для учета неопределенности навыков и динамического обновления рейтингов.

Компьютерная игра Dota 2 представляет класс соревновательных стратегических командных игр, где успех зависит от навыков игроков, их слаженной командной работы, а также от определённых случайных факторов. Для обеспечения баланса соревнований используется рейтинговая система MMR (Matchmaking Rating), аналогичная рейтингу Эло. Система подбирает команды таким образом, чтобы вероятность победы каждой из них была примерно равна. Разница средних MMR двух команд влияет на ожидаемый результат матча. Эмпирические данные показывают, что преимущество в ~300 MMR соответствует примерно 90% вероятности победы более сильной команды.

Рейтинговые модели для командных игр сложнее, чем для дуэльных, и здесь применяются более продвинутые системы, такие как TrueSkill, использующая байесовское обновление вероятностей навыков. Кроме того, в Dota 2 активно развиваются аналитические модели, оценивающие вероятность победы по ходу матча, исходя из игровых параметров – количества золота, опыта, количества убитых героев и других факторов.

Подводя итог, теория вероятностей и математическая статистика предоставляют единый язык и инструментарий для анализа самых разных игр и соревновательных систем. Через примеры покера, шахмат и Dota 2 показано, как вероятностные модели позволяют оценивать шансы на победу и вырабатывать оптимальные стратегии. В эпоху больших данных и развитой игровой аналитики применение теории вероятностей становится важнейшим инструментом прогнозирования и стратегического анализа в играх и спорте.