Лабораторный анализ сигнальной игры с ассиметричной информацией

Laboratory analysis of a signal game with asymmetric information

Kirill Pushkarev

master,  Moscow Institute of Physics and Technology, Russia, Moscow

Аннотация. Целью исследования является нахождение равновесия дискретного отклика для рассматриваемой игры. Проблемой является вычисление данного равновесия для общего случая игры. В общем случае получается, что у продавца есть бесконечное количество чистых стратегий, которым он может следовать. Это приводит к системе, состоящей из бесконечного количества уравнений, которую решить даже на компьютере представляется проблемой.

Для решения этой проблемы в исследования был рассмотрен упрощенный дискретный вид игры, когда продавец может выбирать только из нескольких цен, которые, для упрощения, разделены на маленькие, средние и большие цены.

Abstract. The aim of the study is to find the equilibrium of the discrete response for the game in question. The problem is to calculate this equilibrium for the general case of the game. In the general case, it turns out that the seller has an infinite number of pure strategies that he can follow. This leads to a system consisting of an infinite number of equations, which even a computer solves as a problem.

To solve this problem, the study considered a simplified discrete form of the game, when the seller can choose from only a few prices, which, for simplicity, are divided into small, medium and high prices.

Ключевые слова: теория игр; равновесие дискретного отклика; рынок подержанных автомобилей; сигнальная игра.

Keywords: game theory; discrete response equilibrium; used car market; signal game.

Данная работа изучает сигнальные игры с асимметричной информацией.

Сигнальная игра - это вид динамической игры с неполной информацией. Рассмотрим простой вариант игры, в которой задействованы два игрока: R − получатель и S – отправитель.

Бинарную сигнальную игру можно изобразить графически в виде дерева.

В центре расположим ход игрока 0 (Природы). Если игрок 0 "выбирает" тип t₁, то игра идет вверх по дереву и реализуется тип t₁.

Если же игрок 0 "выбирает" тип t₂, то этому действию соответствует ход игры вниз по дереву и реализуется тип t₂. Ниже на рис. 1 изображено дерево бинарной сигнальной игры. На концах дерева должны быть изображены векторы выигрышей игроков.

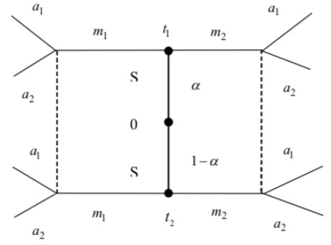
Рисунок 1. Дерево бинарной сигнальной игры

Рынок подержанных автомобилей.

«Рынок подержанных автомобилей» или по другому «Рынок лимонов» – это игра, которая была впервые упомянута в 1970 году в статье американского экономиста Джорджа Акерлофа, в которой было рассмотрено, как качество товаров, продаваемых на рынке, может ухудшаться при наличии информационной асимметрии между покупателями и продавцами, оставляя только «лимоны». В американском сленге «лимон» – это машина, которая считается дефектной только после того, как была куплена.

Предположим, что покупатели не могут отличить качественный автомобиль («персик») от «лимона». Тогда они готовы платить только фиксированную цену за автомобиль, который оценивается усредненной стоимостью «персика» и «лимона» вместе.

Но продавцы знают, какой у них тип автомобиля. Учитывая фиксированную цену, по которой покупатели будут покупать автомобиль, продавцы будут продавать только тогда, когда у них «лимоны», и они покидают рынок, когда у них «персики». В конце концов, когда достаточное количество продавцов «персиков» покинет рынок, средняя готовность покупателей платить снизится, поскольку среднее качество автомобилей на рынке снизилось, что приведет к тому, что еще больше продавцов качественных автомобилей покинут рынок.

Таким образом, цена, предложенная неосведомленному покупателю, создает неблагоприятную проблему выбора, которая вытесняет качественные автомобили с рынка.

Неблагоприятный отбор - это рыночный механизм, который может привести к обвалу рынка.

Статья Акерлофа показывает, как цены могут определять качество товаров, продаваемых на рынке. Низкие цены отгоняют продавцов качественных товаров, оставляя на рынке только лимоны. В 2001 году Акерлоф получил Нобелевскую премию по экономике за исследования по вопросам, связанным с асимметричной информацией.

Статья Акерлофа использует рынок подержанных автомобилей, как пример проблемы неопределенности качества. Подержанный автомобиль - это автомобиль, в котором право собственности передается от одного человека другому после периода использования его первым владельцем и его неизбежного износа. Есть хорошие подержанные автомобили («персики») и бракованные подержанные автомобили («лимоны»), как правило, вследствие ряда не всегда прослеживаемых переменных таких, как стиль вождения владельца, качество и частота обслуживания, а также история аварий. Поскольку многие важные механические детали и другие элементы скрыты от глаз и недоступны для осмотра, покупатель автомобиля заранее не знает, персик это или лимон. Таким образом, лучший выбор покупателя для данного автомобиля заключается в том, что за автомобиль среднего качества покупатель будет готов заплатить только цену автомобиля известного среднего качества. Это означает, что владелец хорошего подержанного автомобиля не сможет получить достаточно выгодное предложение, чтобы оправдать продажу этого автомобиля.

Поэтому владельцы хороших автомобилей не будут размещать свои автомобили на рынке подержанных автомобилей. Отказ от хороших автомобилей снижает среднее качество автомобилей на рынке, заставляя покупателей пересматривать свои ожидания в отношении любого конкретного автомобиля. Это, в свою очередь, мотивирует владельцев умеренно хороших автомобилей не продавать и т. д. В результате рынок, на котором существует асимметричная информация относительно качества, демонстрирует характеристики, аналогичные описанным в законе Грешама: плохое вытесняет хорошее.

Вывод. Данная работа исследует различные виды равновесий в сигнальных играх с асимметричной информацией на примере игры «Рынок подержанных автомобилей». В частности особый интерес представляет равновесие дискретного отклика (QRE). В равновесии с дискретным откликом игроки допускают ошибки при выборе чистой стратегии. Вероятность того, что какая-либо конкретная стратегия будет выбрана, положительно связана с выигрышем от этой стратегии. Другими словами, очень дорогостоящие ошибки маловероятны. В QRE заложен настраиваемый параметр , от которого зависит то, насколько игроки рациональны.

Проблема поиска QRE в сигнальной игры «Рынок подержанных автомобилей» состоит в том, что набор стратегий продавца бесконечен, так как продавец может выбирать любое число из заданного диапазона. Были рассмотрены дискретные случаи игры, которые можно обобщить до общего случая, за исключением вырожденных случаев, когда игроки получают нулевые выигрыши.

В результате исследований было получено, что в равновесии дискретного отклика будет существовать n  m изолированных равновесий, где n - число больших цен, а m - число маленьких цен. Также было получено, что QRE при 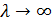 будет сходиться к изолированному СБР, которое соответствует максимальному ожидаемому суммарному выигрышу покупателя и продавца. Также стратегия продавца в изолированном равновесии будет зависить только от большой цены и не будет зависить от маленькой цены.

Обощая эти результаты можно сделать вывод, что QRE для игры со всеми ценами, но без вырожденного случая, будет сходиться к изолированному равновесию, при котором используется цены p₁ → 2 и p₂ → 12, но не равные своим предельным значениям, при которых происходит вырожденный случай.