MS Excel как средство решения задач экономического моделирования и оптимизации
Секция: Экономика

XLI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: общественные и экономические науки»
MS Excel как средство решения задач экономического моделирования и оптимизации
Введение
Планирование производства всегда сопряжено с поиском ответа на вопросы: какую продукцию и в каких количествах выгоднее всего производить из имеющегося сырья, и т.п. Подобные задачи относятся к классу задач линейного программирования – оптимального планирования при условии заданных ограничений. Как правило, это минимизация затрат, максимизация выгоды и оптимизация решений.
На сегодняшний день для создания экономических моделей и решения подобных задач существуют инструменты, позволяющие учитывать множество различных факторов при поиске решения. Один из таких инструментов – надстройка MS Excel «Поиск решения».
В данной статье рассматривается способ решения задачи оптимизации – составление оптимального плана производства – при помощи надстройки «Поиск решения».
Надстройка «Поиск решения»
Поиск решения – это инструмент MS Excel, который помогает решать так называемые задачи оптимизации: минимизация, максимизация или поиск оптимального значения по заранее известным исходным данным.
Кнопка «Поиск решения» находится во вкладке «Данные» (Рисунок 1).

Рисунок 1. Панель инструментов
Если же она на момент запуска программы отсутствует, необходимо произвести следующие действия: запустите главное меню (кнопка “Office” в Excel 2007 или «Файл» в Excel 2010 и 2013), выберите пункт «Параметры», далее перейдите к пункту «Надстройки», нажмите кнопку «Перейти» (Рисунок 2).
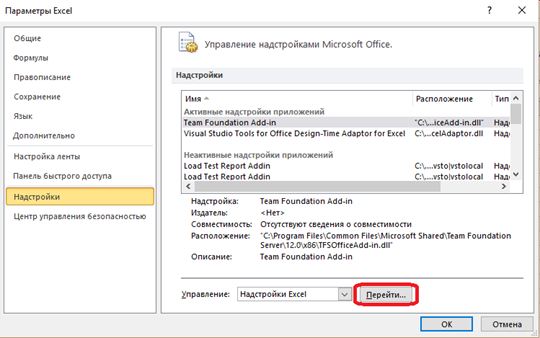
Рисунок 2. Параметры Excel
В появившемся окне отметьте галочкой «Поиск решения» и нажмите ОК (Рисунок 3).
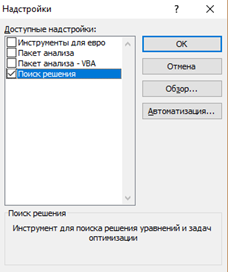
Рисунок 3. Надстройки
После этих действий во вкладке «Данные» появится вкладка «Анализ» с инструментом «Поиск решения».
Постановка задачи
Чтобы получить ответ, необходимо грамотно обозначить условия: исходные данные, ограничения задачи и непосредственно вопрос, который должен разрешиться при решении задачи.
Рассмотрим такую задачу: предприятие занимается изготовлением и продажей канцтоваров (Ручки, Карандаши, Фломастеры, Линейки). Необходимо найти такое соотношение продукции, которое обеспечит получение максимальной прибыли с учетом заданных ограничений.
Задача определена, теперь необходимо определиться с исходными данными. Каждая единица продукции имеет набор характеристик:
· Цена – рыночная цена, за которую покупатель приобретает продукцию.
· Переменные затраты на изготовление – та сумма денег, которую предприятие затрачивает на производство одной единицы продукции. В переменные затраты принято включать не только стоимость сырья, но и заработную плату производственного персонала, административные и управленческие расходы, расходы по реализации продукции, амортизационные отчисления – все расходы, которые меняются прямо пропорционально изменению объемов производства.
· Маржинальный доход – разница между ценой и переменными затратами на изготовление.
· Ограничение по продажам – максимальное количество изделий, которое может быть реализовано за определенный промежуток времени в условиях определенного рынка.
Вне зависимости от специфики товара, каждое предприятие также обладает некоторыми свойствами:
· Ограничения производства – максимальное количество изделий, которое предприятие может произвести вне зависимости от номенклатуры.
· Объем продаж – количество изделий определенной номенклатуры, которое требуется реализовать для получения максимальной прибыли.
· Сумма продаж – это выручка за все продажи определенной продукции (объем продаж умноженный на цену).
· Переменные затраты – это та сумма, которую предприятие потратило на изготовление реализованной продукции (объем продаж умноженный на переменные затраты за единицу изделия).
· Маржинальный доход – разница между полученной выручкой (суммой продаж) и затратами на изготовление продукции (переменные затраты).
· Прибыль – это чистая выручка компании (в нашем случае она равна суммарному маржинальному доходу, т.к. в условиях задачи отсутствуют постоянные затраты).
Предположим, что нам известна вся необходимая информация: цены, переменные затраты (и соответственно маржинальность), ограничения по продажам и ограничения производства. Заполним таблицу имеющимися значениями (Рисунок 1).
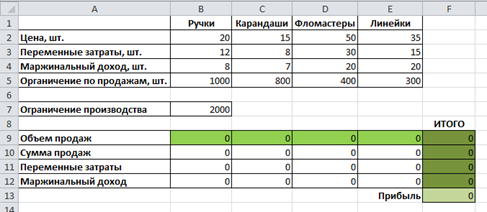
Рисунок 4. Условия задачи
Строка «Объем продаж» – это именно те значения, которые мы будем оптимизировать, так как нам нужно составить оптимальный план производства: определить набор товаров, которые выгоднее всего производить при заданных ограничениях.
Когда условия обозначены, мы можем приступать к решению задачи при помощи «Поиска решений».
Решение задачи при помощи надстройки «Поиск решения» MS Excel
При поиске решения создается математическая модель, состоящая из целевого значения, изменяемых параметров и ограничений. Целевое значение – это тот показатель, который мы стремимся оптимизировать путем подбора значений изменяемых параметров в условиях заданных ограничений. В нашем случае целевое значение – прибыль, которая должна быть максимальной, изменяемые параметры – объем продаж, а ограничения – заранее известные ограничения по продажам, ограничения производства и некоторые другие.

Рисунок 5. Математическая модель задачи
Запускаем инструмент «Поиск решения». Заполняем все необходимые поля: устанавливаем целевую ячейку (должна содержать максимальное значение). В поле «До:» должно быть указано значение «Максимум», так как мы решаем задачу максимизации прибыли, а значит, максимизируем значение целевой ячейки. Далее щелкаем мышкой в поле «Изменяя ячейки» и выбираем изменяемые параметры: В9-Е9 (Рисунок 6).
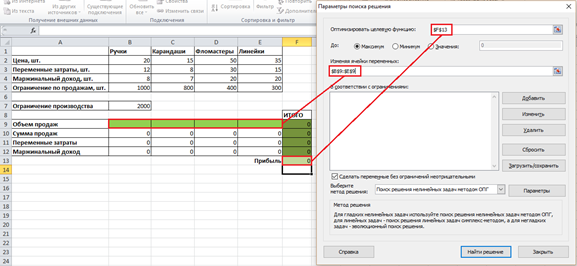
Рисунок 6. Подготовка параметров поиска решения
Также добавим ограничения: нажимаем кнопку «Добавить» справа от поля «Ограничения». Первое ограничение, которое необходимо предусмотреть – объемы продаж могут содержать только положительные значения. На языке Excel это ограничение будет звучать так: $B$9:$E$9 >= 0 (Рисунок 7).
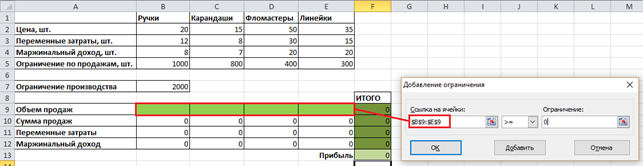
Рисунок 7. Ограничение 1
Второе ограничение – объем продаж не может быть больше, чем ограничение по продажам: $B$9:$E$9 <= $B$5:$E$5 (Рисунок 8).
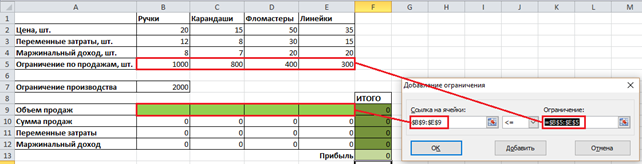
Рисунок 8. Ограничение 2
Третье ограничение – в сумме объем продаж не может быть больше, чем значение ограничения производства: $F$9 <= $B$7 (Рисунок 9).
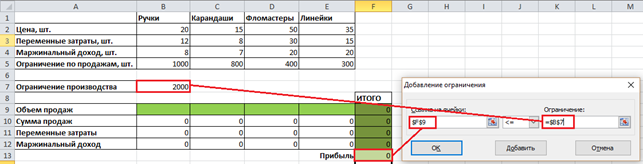
Рисунок 9. Ограничение 3
Таким образом, мы получаем параметры поиска решения (Рисунок 10):
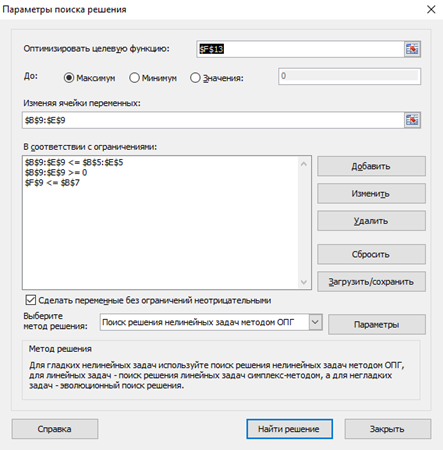
Рисунок 10. Параметры поиска решения
Теперь мы можем найти решение нашей задачи. Нажимаем кнопку «Найти решение» и смотрим результаты:
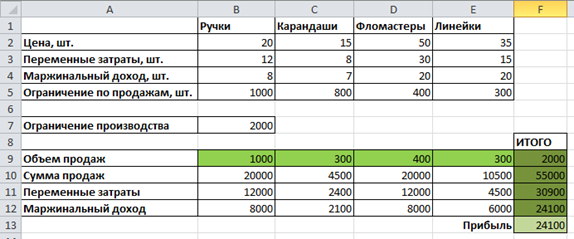
Рисунок 11. Результат применения инструмента «Поиск решения»
Таким образом, мы делаем следующие выводы: при заданных условиях задачи для того, чтобы прибыль была максимальна, выгоднее всего производить 1000 единиц ручек, 300 карандашей, 400 фломастеров и 300 линеек.
Заключение
В данной статье было рассмотрено применение инструмента MS Excel «Поиск решения» для решения задачи максимизации функции. Помимо приведенного примера, эта надстройка подходит для решения огромного количества задач в сфере экономической оптимизации. При помощи «Поиска решения» можно решить практически любую задачу, четко определив параметры математической модели.





