МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЗОДИНАМИКИ КРИЗИСОВ В ЭКОНОМИЧЕСКИХ СИСТЕМАХ

Большинство экономических систем относятся к так называемым сложным системам [3, с. 16]. Для их описания невозможно построить одну универсальную математическую модель. Поэтому разрабатывается целый комплекс моделей, каждая из которых описывает систему на определённом уровне и этапе развития. Особенно сложно моделируется система в момент, когда она переживает кризис. В работах [1, с. 46; 2, с. 18] для описания кризиса используется трехуровневая модель, которая описывает систему на трёх уровнях: макроуровень, микроуровень и мезоуровень. Причем на мезоуровне рассматривается переход системы из одного макросостояния в другое. То есть моделирование кризиса должно происходить на мезоуровне описания сложной экономической системы. В работе [1, с. 50] проведено исследование кризисов на основе мезодинамики развития системы. Однако полученная модель и классификация получились слишком громоздкими и могут дать лишь качественное описание кризиса, что затрудняет их использование для прогнозирования и управления. В данной работе предлагается иной подход к описанию кризисов в сложных системах, основанный на общей теории фазовых переходов.

Под фазой будем понимать микроскопическую однородную часть системы, отделённую от остальных частей системы границей раздела [4, с. 272; 6, с. 44]. При этом одной из макроскопических характеристик системы и фазы является потенциал φ.

С макроскопической точки зрения при фазовом переходе некоторая макроскопическая характеристика меняется скачком. Фазовые переходы делятся на два рода:

1.  Фазовые переходы, при которых первые производные потенциала меняются скачком, называются фазовыми переходами первого рода.

2.  Фазовые переходы, при которых меняются скачком вторые производные от потенциала, называются фазовыми переходами второго рода.

Сам механизм фазовых переходов второго и первого рода различен. При фазовом переходе второго рода одна фаза сменяет другую постепенно, при этом энтропия (информация) изменяется непрерывно. С приближением точки фазового перехода в системе с фазой А в результате флуктуаций появляются флуктуационные зародыши фазы В. Величина среднего зародыша при приближении к точке фазового перехода.будет возрастать. Пусть N — общее число элементов системы, N_А — число элементов системы в фазе А, N_В — число элементов в фазе В. Введем в рассмотрение величину

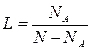.                                                                  (1)

Если величина , то считается, что произошёл фазовый переход второго рода.

Например, к фазовому переходу второго рода близка селекционная работа со стадом КРС, при которой идёт плановая выбраковка. При этом, как правило, при такой работе стадо становится более продуктивным и окупаемым. Заметим, что в отсутствии селекционной работы с течением времени происходит обратный переход.

При фазовом переходе первого рода происходит скачкообразное изменение энтропии (информации). При этом фаза А сменяет фазу В сразу в макроскопическом объеме. При этом фазовый переход не происходит при L=0,5.

Для примера рассмотрим систему, имеющую 3-х мерную размерность [6] [q Î R³].

При этом граница имеет 2-х мерную размерность. Положим, что линейные размеры зародыша — r, тогда изменение свободной энергии в результате его образования будет

.                                                        (2)

Здесь ∆φ = φ_В — φ_А; а, b — положительные коэффициенты.

При малых размерах зародыша новой фазы основной вклад в изменение свободной энергии вносит квадратичный член. Следовательно, образование малых центров новой фазы и их рост является энергетически невыгодным процессом.

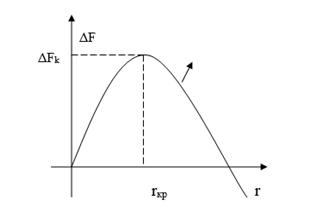
Рисунок 1. График свободной энергии системы

На рисунке 1 показана качественная зависимость изменения свободной энергии от размеров зародыша. При определенном размере r_k (критический размер). При r > r_k рост зародыша новой фазы становится энергетически выгодным процессом.

Критический размер зародыша определяется из уравнения

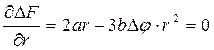,                                            (3)

решая которое, находим

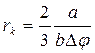.                                                            (4)

Вторая производная при r = r_c равна

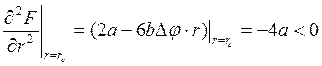,                          (5)

т. е. является существенно отрицательной величиной, что соответствует максимуму изменения свободной энергии.

Следовательно, фазовый переход системы произойдет в том случае, если вероятность образования зародышей новой фазы размеров больших r_c будет существенной. В теории Фольмера-Вебера-Френкеля предложена следующая теория зарождения новой фазы.

Зарождение при фазовом переходе происходит благодаря спонтанному возникновению в метастабильной фазе гетерофазных флуктуаций и их дальнейшей эволюции за счёт последовательного присоединения отдельных элементов системы. Параллельно может идти процесс распада нового центра, так что в самом общем виде процесс образования центров новой фазы можно представить следующим образом

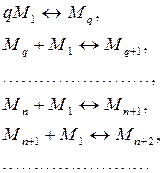                                                      (6)

Здесь M₁ — одиночный элемент системы, M_q — исходная гетерофазная флуктуация, содержащая q элементов, M_n — растущий центр зарождения новой фазы. Распределение зародышей по размерам (или по числу элементов в зародыше) будет определяться формулой:

.                                                     (7)

Здесь M — полное число частиц всех возможных размеров в системе

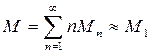.                                                       (8)

T — параметр отвечающий за фазовый переход. При этом полагается, что фазовый переход произойдет в том случае, когда наивероятнейший размер зародыша станет сравнимым с r_c.

Работу экономических систем достаточно сложно выразить через термодинамические функции, используемые в естественных науках. Однако, теорию фазовых переходов можно связать с общим для всех систем принципом максимума информации [5, с. 75]. В частности, показано, что уравнение Фоккера-Планка, стационарное решение которого используется для описания фазовых переходов, может быть получено из принципа максимальной информации. Приращение информации в системе вблизи точек фазового перехода практически совпадают с изменениями информации и приращением информации, относящимся к параметрам порядка.

Так для фазового перехода второго рода изменение информации при одном параметре порядка определяется формулой

.                                              (9)

Для фазового перехода первого рода

.                                  (10)

Здесь

.

f(x) = N exp{αx² - bx⁴} — для уравнения,

f(x) = N exp{αx² - bx⁴ — gx⁶} — для уравнения.

Очевидно, что в сложных социальных системах могут возникать кризисы, которые имеют черты и фазовых переходов первого рода, и фазовых переходов второго рода, вызываемые сразу несколькими причинами. Математическое описание таких кризисов является отдельной сложной проблемой и в данной работе не рассматривается.

Подведём итоги проведённых исследований.

1.  Кризисное состояние в сложных социальных системах характеризуется максимальным значением информации Шеннона, подсчёт которой во многих случаях проводится достаточно просто.

2.  Кризисы можно разделить на две группы, соответствующие фазовым переходам первого и второго рода.

Кризисы, соответствующие фазовым переходам второго рода, являются обратимыми и управляемыми на протяжении всего своего развития.

На рисунках 2, 3 кризисы первого и второго родов иллюстрируются на смене макросостояний взаимоотношений между субъектами рынка [7, с. 64]. Здесь  — состояние содействия,  — состояние противодействия,  — состояние эксплуатации,  — нейтралитет,  — банкротство. Подробное описание каждого состояния можно найти в работах [1, с. 83; 7, с. 38].

Рисунок 2. Схема кризиса второго рода

Кризисы, соответствующие фазовым переходам первого рода, проходят по более сложной схеме. При этом существуют этапы, на которых кризис является управляемым, слабо управляемым и практически неуправляемым (рисунок 3).

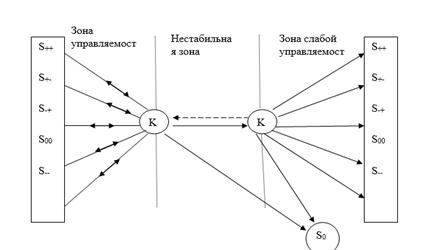
Рисунок 3. Схема кризиса первого рода

3.  Для кризисов, соответствующих фазовому переходу первого рода, закон приращения информации даётся формулой (1). Для кризисов, соответствующих фазовому переходу второго рода, — формулой (2).

Можно предположить, что кризисы первого рода развиваются в агрессивной среде, поэтому они будут типичны для отношений конкуренции и жесткой эксплуатации. В то же время для отношений содействия должны быть свойственны кризисы второго рода.

Термодинамический подход к описанию кризиса не позволяет заранее определить, какой из параметров является его причиной, поскольку принцип максимума информации является достаточно общим. Поэтому для уточнения того, к чему ведет кризис, между субъектами рынка требуются дополнительные исследования. Их можно провести с исследованием известной модели марковского процесса с непрерывным временем и дискретными состояниями.

Список литературы:
1.    Аржаков Н.В., Новосельцев В.И., Редкозубов С.А. Управление динамикой рынка: системный подход. — Воронеж. — Изд-во Воронеж. гос. Ун-та, 2004, — 192 с.
2.    Бурков В.Н. Основы математической теории активных систем. — М. Наука, 1977, — 227 с.
3.    Пугачев В.С., Синицын И.Н. Теория стохастических систем. Учеб. пособие. — М; Логос. 2004. — 1000 с.
4.    Сивухин Д.В. Термодинамика и молекулярная физика. Учебное пособие для вузов. — М; Наука, ФИЗМАТЛИТ, 1990, — 592 с.
5.    Хакен Г. Информация и самооранизация. — М: КомКнига. 2005. — 248 с.
6.    Хотченков А.Г. Гетерофазные флуктуации в сегнетоэлектриках. Смоленск 1990, — 170 с.
7.    Юденков А.В., Скородулина Е.Ю. Моделирование конфликтных ситуаций в менеджменте методами нечеткой логики. Смоленск: ФГБОУ ВПО «Смоленская ГСХА», 2012, — 90 с.