Определение минимального значения перерегулирования системы с применением генетического алгоритма.

Основы теории генетических алгоритмов сформулированы Дж. Г.Холландом в основополагающей работе и в дальнейшем были развиты рядом других исследователей. Наиболее известной и часто цитируемой в настоящее время является монография Д.Голдберга, где систематически изложены основные результаты и области практического применения генетических алгоритмов.

Генетический алгоритм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе. Является разновидностью эволюционных вычислений, с помощью которых решаются оптимизационные задачи с использованием методов естественной эволюции, таких как наследование, мутации, отбор и кроссинговер. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.

Одна из целей построения факторной модели является нахождение экстремумов. В этой лабораторной работе требуется определить минимальное значение перерегулирования системы. Для этого был применен генетический алгоритм.

В качестве начальных значений для генетического алгоритма были взяты случайные значения T из допустимого диапазона (таблица 6).

Таблица 1.

Начальные значения

Генетический алгоритм использует двоичную запись числа, поэтому выбранные значения были умножены на 100. Также для них были вычислены значения σ(T) и приспособленность, которая рассчитывается по следующей формуле:

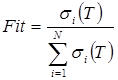                                                                                                              (1)

где N – количество особей.

Все значения для начальной популяции приведены в таблице 7.

Разрядность для представления чисел в двоичной форме равняется 11. Этого достаточно, чтобы задать диапазон чисел для нахождения минимума (максимальное значение T в таком случае будет равно 211=4096).

Для реализации генетического алгоритма в данной лабораторной работе была составлена программа в среде моделирования SciLab. Алгоритм реализован следующим образом:

1. На каждой итерации происходит скрещивание 1 и 2 особи. В результате в них меняются гены в позициях 1, 4, 5, 8.
2. Также скрещиваются 3 и 4 особи. В них меняются гены в позициях 2, 3, 5, 6.
3. После завершения скрещивания происходит мутация в случайной особи и в случайном гене, в результате чего выбранный ген изменяется на противоположный.
4. Действия 1-3 продолжаются до тех пор, пока перерегулирование, вычисляемое на каждой итерации, больше заданной допустимой погрешности (ε).

Выполнение генетического алгоритма представлена ниже.

Далее будут приведены итерации генетического алгоритма для выбранной погрешности ε=0.1 (таблица 3-7).

Таблица 2.

Начальная популяция генетического алгоритма

На 1 итерации произошла мутация в 1 особи в 1 гене (таблица 3).

Таблица 3.

Итерация 1 для ε=0.1

На 2 итерации произошла мутация в 3 особи в 3 гене (таблица 4).

Таблица 4.

Итерация 2 для ε=0.1

На 3 итерации произошла мутация во 2 особи в 6 гене (таблица 5).

Таблица 5.

Итерация 3 для ε=0.1

На 4 итерации произошла мутация во 2 особи в 4 гене (таблица 6).

Таблица 6.

Итерация 4 для ε=0.1

Минимум функции был найден за 4 итерации и он равен σ_min =0.087379. Такое значение перерегулирования достигается при T_min = T*_min/100=1199/100=11.99.

Также был произведен эксперимент с уменьшенной допустимой погрешностью ε=0.01. Один из лучших полученных результатов для такой точности отображен в таблице 7.

Таблица 7.

Итерация 19 для ε=0.01

Алгоритм для погрешности ε=0.01 за 19 итераций нашёл минимум функции равный 0.001067, при значении T равным 18.73.

В данной лабораторной работе было исследовано влияние факторов T и k на перерегулирование математической модели системы.

Был составлен факторный план и на его основе проведены эксперименты, по результатам которых была построена факторная модель, представляющая из себя функцию, зависящую от двух переменных (T и k). В ходе построения, оказалось, что влияние фактора k в данном варианте лабораторной работы незначительное и им можно пренебречь.

Полученная факторная модель была проверена на адекватность. Для этого был использован t-критерий Стьюдента. Оказалось, что полученная модель адекватна и её погрешность составляет 0,0038.

Нахождение минимума функции полученной факторной модели при различных значениях допустимой погрешности было осуществлено с помощью генетического алгоритма. При значении погрешности ε=0.1, минимум был найден за 4 итерации и равен 0.087379. При ε=0.01 минимум был найден за 19 итераций и равен 0.001067.