Расчёт балки на жесткость и прочность
Секция: Технические науки

XXVI Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Расчёт балки на жесткость и прочность
В сфере электроэнергетики при выполнении устройства заземления зданий главного распределительного щита, распределительный щит и общеподстанционный пункт управления, а также подобных сооружений и зданий, которые содержат вторичное оборудование и системы связи, используют кастовую сеть заземления. Она включает в себя значительное число взаимосвязанных проводников, при этом используются все существующие металлические конструкции, как вертикальные, так и горизонтальные, например, балки.
Для примера рассмотрим горизонтально расположенную балку АВ (рис.1) постоянного поперечного сечения, сделанную из однородного материала. Ось симметрии балки указана на рисунке 1 пунктирной линией. Предположим, что под влиянием сил, которые действуют на балку в вертикальной плоскости, содержащей ось симметрии, балка прогибается (рис.2).
|
Рисунок 1. Балка |
Рисунок 2. Прогиб балки |
Действующие силы могут быть обусловлены весом балки, внешне приложенной нагрузкой или как той, так и другой силами вместе. Понятно, что под действием сил ось симметрии будет искривляться. Обычно искривленную ось симметрии называют упругой линией. Определение формы этой линии играет важную роль в теории упругости [1, c.69].
Отметим, что существуют различные типы балок в зависимости от способов их крепления или опоры. Например, на рисунке 3 изображена балка, у которой конец А жестоко закреплен, а конец В свободен. Такая балка называется консольной балкой. На рисунке 4 показана балка, лежащая свободно на опорах А и В.
|
Рисунок 3. Консольная балка |
Рисунок 4. Свободно лежащая балка |
Еще один тип балок с опорами показан на рисунке 5. Существуют и различные способы приложения внешних нагрузок. Например, рисунке 3 показана равномерно распределённая нагрузка. Конечно, нагрузка может быть и переменной вдоль всей длины балки или некоторой ее части (рис.4). На рисунке 5 указан случай сосредоточенной нагрузки.
Рисунок 5. Балка со сосредоточенной нагрузкой
Рассмотрим горизонтальную балку ОА (рис.6). Пусть ее ось симметрии (показанная на рисунке пунктиром) лежит на оси х, где за положительное направление выбирается направление в право от точки О, являющейся началом координат.

Рисунок 6 .Горизонтальная балка
За положительное направление на оси у выберем направление вниз от точки О. Под действием внешних сил F1, F2, … (и веса балки, если он большой) ось симметрии искривляется в упругую линию, которая показана на рисунке 7 пунктиром. Смещение упругой лини оси х называется прогибом балки в положении х. Таким образом, если известно уравнение упругой линии, то всегда можно указать и прогиб балки. Ниже мы покажем, как это может быть сделано практически.

Рисунок 7. Прогиб балки по x
Обозначим через М(х) изгибающий момент в вертикальном поперечном сечении балки с координатой х. Изгибающий момент определяется как алгебраическая сумма моментов тех сил, которые действуют с одной стороны балки в положении х. При подсчете моментов будем считать, что силы, которые действуют на балку снизу вверх, дают отрицательные моменты, а силы, действующие сверху в низ, дают положительные моменты.
В сопротивлении материалов доказывается, что изгибающий момент в положении x связан с радиусом кривизны упругой линии соотношением
![]() (1)
(1)
где E – модуль упругости Юнга, который зависит от материала, J - момент инерции поперечного сечения балки в положении x относительно горизонтальной прямой, проходящей через центр тяжести этого поперечного сечения. Произведение EJ обычно называют жесткостью при изгибе; ее величину в дальнейшем будем считать постоянной.
Теперь, если предположить, что балка лишь слегка прогибается, что часто бывает на практике, то угловой коэффициент y’ упругой линии будет очень мал, и поэтому вместо уравнения (1) можно рассматривать приближенное уравнение
![]() (2)
(2)
Чтобы показать, как на практике используется уравнение (2), рассмотрим следующую задачу. Горизонтальная однородная стальная балка длины l, свободно лежащая на двух опорах, прогибается под действием собственного веса, равного p кгс на единицу длины. Требуется найти уравнение упругой линии и максимальный прогиб балки.
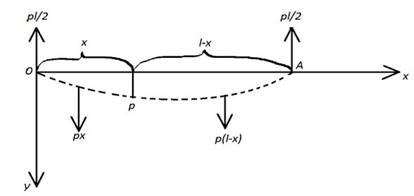
Рисунок 8. Упругая линия балки
На рис. 8 упругая линия показана пунктиром. Поскольку балка является двухопорной, то каждая из опор создаёт направленную вверх реакцию, равную половине веса балки (равную pl/2). Изгибающий момент M(x) есть алгебраическая сумма моментов этих сил, действующих на балку с одной стороны от точки Q. На расстоянии x от точки Q сила pl/2 действует на балку снизу вверх и создаёт отрицательный момент. Сила же px, которая действует на балку сверху вниз на расстоянии x/2 от точки Q, создаёт положительный момент. Таким образом, суммарный изгибающий момент в точке Q задаётся формулой
![]() (3)
(3)
Если же рассматривать действие сил справа от точки Q, то в этом случае на расстоянии ![]() от точки Q на балку действует сверху вниз сила p(l-x), которая создаёт положительный момент. Отрицательный же момент создаёт сила pl/2, которая действует на балку снизу вверх на расстоянии l-x от точки Q. Суммарный изгибающий момент подсчитывается в данном случае по формуле
от точки Q на балку действует сверху вниз сила p(l-x), которая создаёт положительный момент. Отрицательный же момент создаёт сила pl/2, которая действует на балку снизу вверх на расстоянии l-x от точки Q. Суммарный изгибающий момент подсчитывается в данном случае по формуле
![]() (4)
(4)
Как показываются формулы (3) и (4), изгибающие моменты и обоих случаях оказываются равными. Теперь, зная, как находится изгибающий момент, легко выписать и основное уравнение (2), которое в нашем случае принимает вид
![]() (5)
(5)
Учитывая же, что на концах O и A балка не прогибается, для нахождения y из уравнения (5) воспользуемся условиями на концах балки:
y=0 при x=0 и y=0 при x=l.
А тогда интегрирование уравнения (5) с учётом последних условий даёт [2, c.148]
![]() (6)
(6)
Уравнение (6) является уравнением упругой линии. Формула (6) используется на практике для определения максимального прогиба. Так, в нашем конкретном случае, основываясь на соображениях симметрии (это можно сделать и прямыми вычислениями), находим, что максимальный прогиб будет при ![]() и равен он
и равен он ![]() где
где ![]()