Решение задачи распараллеливания вычисления ортогональных функций Якоби

Для данной работы были выбраны ортогональная функция Якоби, ее N-ая производная и неопределенный интеграл n-ого рода, представленные формулами 1,2 и 3 [1]:

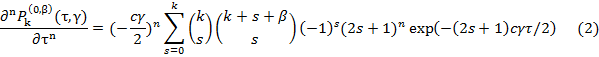
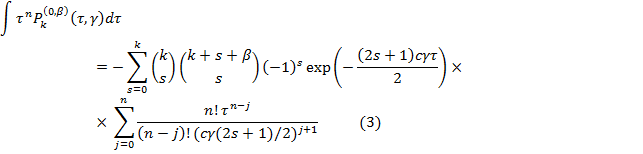
Количество строк матрицы N, определяется следующим образом:

,

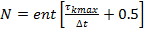где  вычисляется, как

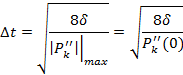
Где τ определяется моментом, когда функция перестает выходить из диапозона ±δ.

Для вычисления биномиального коэффициента используется формула 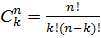, в которой для вычисления факториала используется Гамма функция, т.к. 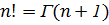. Для вычисления Гамма-функции использовалось приближение Ланцоша.

Распараллеливание вычислений было реализовано по модели MapReduce. Каждая реализация вычислений представляет собой работу, обычно состоящую из двух частей: Map и Reduce.

В первой работе выполняются вычисления для нахождения значений одной из трех функций: ортогональной функции Якоби, ее производной или интеграла. Изначально формируется входной файл, содержащий строки (для каждого порядка функции от 1 до выбранного пользователем) следующего вида: выбранный тип функции, порядок функции k, количество временных отсчетов N, γ, β, временной интервал между соседними отсчетами Δτ (значение). На стадии Map весь временной интервал разбивается на части по несколько отсчетов и к параметрам добавляются границы каждой части, результат передается на следующую стадию Map, где вычисляется значение функции порядка k для каждого из отсчетов полученной части временного интервала.

Полученный массив значений функции преобразуется в прямоугольную матрицу, над которой выполняются остальные работы. Вторая работа выполняет транспонирование матрицы. Во время ее запуска в качестве глобального параметра передается количество строк матрицы. На вход Map поступают значения вида: номер строки матрицы (ключ), строка матрицы (значение), на выходе для каждого элемента строки формируется результат: номер столбца (ключ), номер строки и значение элемента(значение). Далее результат агрегируется по значению ключа и на вход Reduce поступают все элементы матрицы одного столбца, результат записывается в виде: номер столбца (ключ), строка транспонированной матрицы (значение).

Третья работа состоит из последовательного выполнения двух работ: работы по транспонированию исходной матрицы и работы по умножению исходной матрицы на транспонированную. При запуске умножения MapperA (для исходной матрицы) для каждого элемента полученной строки матрицы формирует результат в виде k строк, где k принимает значения от 0 до количества столбцов транспонированной матрицы: номер строки элемента и k(ключ), идентификатор матрицы (для восстановления порядка следования матриц при умножении), номер столбца элемента, значение элемента (значение). А MapperB (для транспонированной матрицы) - в виде i строк, где i принимает значения от 0 до количества строк исходной матрицы: i и номер столбца элемента (ключ), идентификатор матрицы, номер строки элемента, значение элемента (значение). Reducer все полученные значения по идентификатору матрицы относит либо к строке исходной матрицы, либо к столбцу транспонированной, а после выполняет умножение сформированной строки на столбец и отправляет значение элемента результирующей матрицы и его позицию.

Программа, реализующая параллельные вычисления была написана на языке Java. Результаты параллельных вычислений представлены в виде таблиц 1-3 и в виде графиков 1-3. Время вычислений указано в миллисекундах.

Таблица 1.

Параллельное вычисление функции Якоби

Таблица 2.

Параллельное вычисление интеграла функции Якоби

Таблица 3.

Параллельное вычисление производной функции Якоби

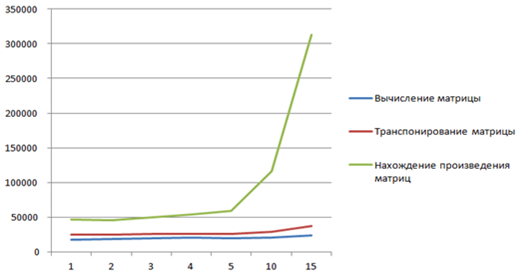
Рисунок 1. Параллельное вычисление функции Якоби

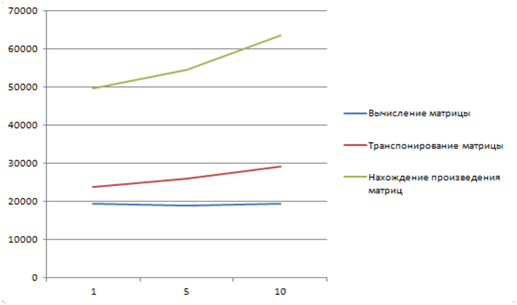
Рисунок 2. Параллельное вычисление производной функции Якоби

Рисунок 3. Параллельное вычисление интеграла от функции Якоби