СРАВНЕНИЕ АЛГОРИТМОВ СОРТИРОВКИ: АНАЛИЗ ЭФФЕКТИВНОСТИ

Сортировка является одной из фундаментальных операций в области компьютерных алгоритмов. Она позволяет упорядочить набор данных в заданном порядке и является неотъемлемой частью множества приложений, начиная от базовых операций с данными до сложных алгоритмов машинного обучения и анализа данных.

Существует множество алгоритмов сортировки, каждый из которых имеет свои особенности и характеристики. Одной из важных задач при выборе алгоритма сортировки является анализ и сравнение их эффективности. Понимание производительности алгоритмов сортировки позволяет разработчикам искусно выбирать наиболее подходящий алгоритм для конкретных ситуаций, учитывая ограничения по времени и памяти.

Мы рассмотрим некоторые из наиболее часто используемых методов сортировки, применяя Python как язык программирования для иллюстрации:

1. Сортировка пузырьком (Bubble Sort) — это алгоритм сортировки, который сравнивает два соседних элемента массива и меняет их местами, пока они не будут в нужном порядке, имеет квадратичную сложность O(n²) в среднем и худшем случаях и O(n) в лучшем случае, когда массив уже отсортирован [1]. Обычно используется для сортировки небольших массивов.
2. Алгоритм сортировки пузырьком работает следующим образом:

1. Начинаем с первого элемента массива;
2. Сравниваем первый элемент с вторым. Если первый элемент больше второго, меняем их местами;
3. Переходим к следующему элементу массива. Снова сравниваем его со следующим и меняем местами, если он больше;
4. Продолжаем этот процесс до конца массива. Таким образом, самый большой элемент перемещается на последнее место в первой итерации;
5. Повторяем те же шаги для оставшихся элементов массива, исключая уже отсортированные. После каждой итерации очередной наибольший элемент становится на свое место;
6. Алгоритм заканчивается, когда все элементы массива отсортированы.

Пример сортировки пузырьком на языке Python представлен на рисунке 1

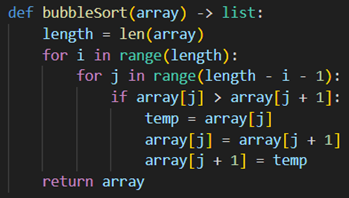
Рисунок 1. Сортировка пузырьком на языке Python

2. Сортировка вставками (Insertion Sort) — это алгоритм сортировки, который постепенно строит отсортированную последовательность, проходя по списку и вставляя каждый элемент в правильное место. Он обладает линейной сложностью O(n) в лучшем случае (когда список уже отсортирован) и квадратичной сложностью O(n²) в среднем и худшем случаях [2].

1. Алгоритм сортировки вставками работает следующим образом;
2. Считаем первый элемент массива отсортированным;
3. Берем следующий элемент и сохраняем его в отдельной переменной (назовем ее ключ);
4. Сравниваем ключ с элементами в отсортированной части массива, начиная с последнего. Если ключ меньше текущего элемента, то сдвигаем текущий элемент на одну позицию вправо. Повторяем этот процесс, пока не найдем элемент, который меньше или равен ключу, или не дойдем до начала массива;
5. Вставляем ключ на найденное место или в начало массива, если он меньше всех элементов в отсортированной части;
6. Повторяем шаги 2-4 для оставшихся элементов в неотсортированной части массива, пока не отсортируем весь массив.

Пример сортировки вставками на языке Python представлен на рисунке 2

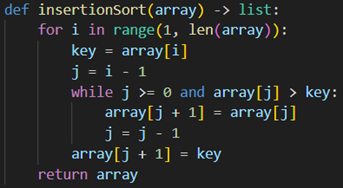
Рисунок 2. Сортировка вставками на языке Python

3. Сортировка выбором (Selection Sort): этот алгоритм сортировки на каждом шаге находит минимальный элемент из неотсортированной части списка и меняет его местами с первым неотсортированным элементом. Сложность алгоритма сортировки выбором составляет O(n²) в лучшем, среднем и худшем случаях, так как на каждой итерации требуется пройти по всему неотсортированному массиву [1]. Этот алгоритм не подходит для больших объемов данных, так как он работает очень медленно. Однако он прост в понимании и реализации и не требует дополнительной памяти.

Алгоритм сортировки выбором работает следующим образом:

1. Считаем первый элемент массива наименьшим;
2. Сравниваем наименьший элемент с остальными элементами массива. Если находим элемент меньше наименьшего, запоминаем его как новый наименьший;
3. После прохода по всему массиву меняем местами наименьший элемент с первым элементом неотсортированной части массива. Таким образом, наименьший элемент оказывается на первом месте отсортированной части массива;
4. Повторяем шаги 1-3 для оставшихся элементов неотсортированной части массива, пока не отсортируем весь массив.

Пример сортировки выбором на языке Python представлен на рисунке 3

Рисунок 3. Сортировка выбором на языке Python

4. Сортировка слиянием (Merge Sort): это эффективный алгоритм сортировки, который основан на принципе "разделяй и властвуй". Он разбивает список на две половины, рекурсивно сортирует каждую половину, а затем объединяет их, чтобы получить отсортированный список. Сортировка слиянием имеет сложность O(n log n) во всех случаях [3]. Этот алгоритм эффективен для больших объемов данных, но требует дополнительной памяти для хранения временных массивов.

Алгоритм сортировки слиянием работает следующим образом:

1. Если массив состоит из одного элемента, то он уже отсортирован и возвращается как результат;
2. Если массив состоит из более чем одного элемента, то он делится на две равные или почти равные части;
3. Каждая часть сортируется рекурсивно с помощью сортировки слиянием;
4. Две отсортированные части объединяются в один отсортированный массив с помощью процедуры слияния, которая сравнивает элементы двух частей и копирует меньший элемент в результирующий массив, пока обе части не будут исчерпаны.

Пример сортировки слиянием на языке Python представлен на рисунке 4

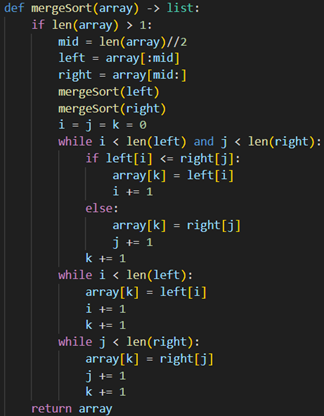
Рисунок 4. Сортировка слиянием на языке Python

5. Быстрая сортировка (Quick Sort): это один из самых быстрых алгоритмов сортировки в среднем случае. Он также использует принцип "разделяй и властвуй", выбирая опорный элемент и разделяя список на две части: элементы, меньшие опорного, и элементы, большие опорного. Затем он рекурсивно сортирует каждую часть. Быстрая сортировка в среднем случае имеет сложность O(n log n), но в худшем случае может иметь квадратичную сложность O(n²) [4].

Быстрая сортировка работает следующим образом:

1. Если массив состоит из одного или нуля элементов, то он уже отсортирован и возвращается как результат;
2. Если массив состоит из более чем одного элемента, то выбирается один элемент в качестве опорного. Это может быть любой элемент массива, но от выбора опорного зависит эффективность алгоритма. Существуют разные способы выбора опорного элемента, например, первый, последний, средний, случайный или медианный элемент массива;
3. Переставить элементы массива так, чтобы все элементы, меньшие опорного, оказались слева от него, а все элементы, большие или равные опорному, оказались справа от него. Это называется разбиением массива. Существуют разные способы выполнения разбиения, например, схема Ломуто, схема Хоара, схема Тарьяна и другие;
4. Рекурсивно применить быструю сортировку к левой и правой части массива, не включая опорный элемент;
5. Объединить отсортированные левую и правую части массива с опорным элементом в один отсортированный массив.

Пример быстрой сортировки используя схему разбиения Хоара на языке Python представлен на рисунке 5

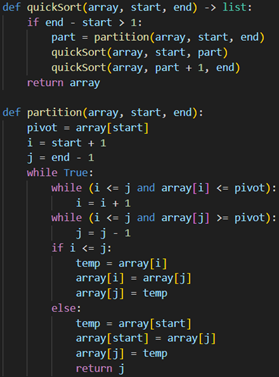
Рисунок 5. Быстрая сортировка используя схему разбиения Хоара на языке Python

Для сравнения различных методов сортировки в Python мы воспользуемся библиотекой time. Эта библиотека позволяет замерять время выполнения кода, что полезно при оценке производительности алгоритмов.

У нас есть список из 441 числа, который мы будем сортировать. Для каждого метода сортировки выполним десять итераций и замерим среднее время выполнения, которое будет представлено в таблице 1.

Таблица 1.

Сравнение различных методов сортировки

Таким образом, при выборе метода сортировки рекомендуется использовать быструю сортировку или сортировку слиянием для достижения наилучшей производительности.