Математическое моделирование цементации стали

Для расчета параметров слоя после диффузионного газовой цементации стали при заданных параметрах технологического процесса газовой цементации разработана математическая модель режима газовой цементации стали, получены уравнения зависимости толщины слоя от совокупности исходных данных. С помощью математического моделирования на ЭВМ изучено влияние различных факторов на процесс газовой цементации стали, являющейся наиболее распространенным процессом химико-термической обработки [1. с. 37‒78] , [2, с 70–75], [3, с 17–28].

В современном машиностроении для повышения долговечности деталей широко используется газовая цементация.

Для полного химико-термического расчета процесса диффузионного насыщения надо знать теплоту хемосорбции и десорбции насыщающих веществ и продуктов реакции; характер изменения концентрации с увеличением степени заполнения поверхности; энергию активации хемосорбции веществ, находящихся в реакционном объеме; теплоту образования термодинамически возможных фаз и ряд других констант. Поэтому в настоящее время нет полной математической модели процесса химико-термической обработки, в которой учитывались бы все перечисленные явления. Для газовой цементации стали измеренных констант достаточно, чтобы связать диффузионные характеристики, активность среды и распределение углерода по диффузионной зоне, т.е. создать в первом приближении математическую модель для управления процессом.

Концентрация углерода на поверхности и характер его распределения по глубине слоя определяют усталостную прочность, прочность при изгибе, контактную выносливость и износостойкость цементованных и термически обработанных деталей.

Для стационарного потока в направлении диффузии количество диффундирующего вещества q, переходящее за единицу времени через единицу площади, пропорционально градиенту концентрации (первый закон Фика)

q = -D × ∂С/∂х                                                 (1)

где С  – концентрация диффундирующего вещества;

 х – координата.

Для нестационарного потока справедлив второй закон Фика – уравнение для скорости изменения концентрации в определенной точке сечения

∂С/∂τ = ∂²С/∂х²                                                 (2)

При химико-термической обработке в большинстве случаев диффузионный слой много меньше сечения изделия, поэтому уравнение (2) решаем для полубесконечного твердого тела, простиравшегося от х = 0 до х = ∞. Если коэффициент диффузии не зависит от концентрации и концентрация на поверхности не меняется, то решение уравнения (2) имеет вид

С_(x,τ) = С₀ erfc x/(2×),                               (3)

где erfc(х)  трансцендентная функция

erfc(х) = 1 - .                                  (4)

Температурная зависимость коэффициента диффузии выражается уравнением

D = D₀ e^(-E/RT)                                                    (5)

где D –множитель перед экспонентой

E – энергия активации диффузии, кал/г. атом;

R – газовая постоянная (≈2 кал/г. атом);

T – температура, К.

Решение усложняется, если коэффициент диффузии зависит от концентрации углерода в аустените(% массы С)

D = (0,04 + 0,08×С) е ^–31350/RT                                   (6)

Для газовой цементации стали наиболее распространена эндотермическая атмосфера, позволяющая регулировать углеродный потенциал. Ее получает путем крекирования природного газа в генераторах с большим недостатком воздуха (коэффициент избытка воздуха α = 0,25). Эта реакция идет с поглощением тепла, поэтому атмосфера называется эндотермической. Ее средний состав: 20% СО, 40% Н₂, ~40% N₂, не более 1% CО₂; не более 1,5% СН₄; 0,1–2% Н₂О. Изменяя коэффициент избытка воздуха α, можно подбирать условия равновесия и создавать атмосферу с требуемым углеродным потенциалом. Состав ее регулируют с помощью датчиков, регистрирующих содержание Н₂О (или CО₂) в печной атмосфере, и системы управления соотношением воздуха и газа, поступавших в камеру крекирования.

Эндотермическая атмосфера имеет низкую науглероживающую способность. Для повышения углеродного потенциала к ней добавляют 5–10% городского газа, содержащего в основном СН₄. Выделение углерода при цементации в такой смеси происходит по следующим реакциям

2 СО ↔ CО₂ + С(γ - Fе);                                  (7)

СО + Н₂ ↔ Н₂О + С(γ - Fе);                             (8)

СН₄ ↔ 2Н₂ + С(γ - Fе).                                    (9)

Видно, что СО и СН₄ являются науглероживающими металл компонентами газовой снеси, а CО₂ и пары воды – обезуглероживающими компонентами. Водород играет двоякую роль: с одной стороны, он способствует науглероживанию (реакция (8), а с другой – тормозит распад CH₄, реакция (9). Таким образом, эта атмосфера (в зависимости от соотношения парциальных давлений ее компонентов) может быть по отношению к стали данного состава равновесной, науглероживающей или обезуглероживающей.

Из условия равновесия реакций (7) – (9), заменив парциальное давление углерода в газовой фазе и металле термодинамической активностью α_c, получим

К₁ = (P_CO2/P²_CO)×a_c;                                            (10)

К₂ = (P_H2O/(P_CO×P_H2))×a_c;                                    (11)

К₃ = (P²_H2/P²_CH4)×a_c,                                          (12)

где  К₁, К₂, К₃ – константы равновесия реакций (7), (8), (9);

P – парциальное давление соответствующих газов в безразмерном виде (отнесено к стандартному состоянию (2 атм);

a_c – активность углерода в газовой фазе.

Из (10) следует, что

a_c = К₁ × (P²_CO/P_CO2).                                       (13)

Способность атмосферы к науглероживанию увеличивается как квадрат парциального давления CO (науглероживающего компонента) и уменьшается линейно с ростом парциального давления СO₂ (обезуглероживающего компонента).

По условию равновесия активности углерода в атмосфере a_c и металле a_c` равны

a_с = a_с ^`= К₁ × (P²_CO/P_CO2)                                (14)

Активность и содержание углерода в аустените объединены

a_с = g_с × А × С’_c’                                                        (15)

где a_с – активность углерода;

С’_c – содержание углерода в аустените в %(массы);

g_с –активность углерода в аустените;

А ≈ 4,67×10^-2 –перевод весовых процентов в атомные доли, тогда

С’_c’ = (1/g_с × А) × К₁ × (P²_CO/P_CO2).                                     (16)

Чтобы найти парциальные, давления P_CO и P_CO2 в газовой среде, содержащей СО, СО₂, СН₄ и Н₂, следует учитывать условия равновесия частных систем (CO – СО₂ и СН₄ – Н₂), равенство активностей углерода в них, т.e.

a_с = К₁ × (P²_CO/P_CO2)  =  К₂ × (P_CН4/P² _Н2)                                 (17)

Углеродный потенциал определяет характер взаимодействия атмосферы с металлом. Науглероживание металла идет, пока углеродный потенциал атмосферы выше концентрации углерода в цементируемых деталях. Скорость перехода углерода из газовой среды ограничена, и содержание углерода на поверхности стали изменяется постоянно_, асимптотически приближаясь к состоянию равновесия поверхности с окружающей средой.

При ограниченной скорости подачи количество элемента d_m, поступающего из газа на поверхность изделий, пропорционально разности равновесному содержанию на поверхности С_(0,∞), содержанию в данный момент С_(0,τ), площади поперечного сечения F и времени диффузии

d_m = β × [С_(0,∞)- С_(0,τ)] × F×  dτ                                   (18)

где β – коэффициент скорости передачи элемента от окружающей среды к поверхности детали. Если выразить m в граммах, F – в см², τ – в секундах и С – в г/см³, то размерность β – в см/с.

Если концентрация углерода – в процентах массы, то используют величину β’ = 0,078 × β [г/(см² × с × %С)], показывающую, сколько углерода выделятся в единицу времени на поверхности металла площадью 1 см² при разности между углеродным потенциалом атмосферы и концентрацией в металле, равной 1% массы.

Если концентрация углерода не превышает предела его растворимости в аустените, то (с учетом конечной скорости поглощения) изменение относительной концентрации

Q_(x,τ)=(C_x - C_исх)/(C_пред - C_исх)

в исходном материале описывается следующем уравнением

Q_(x,τ) = (C_{x, τ} - C_исх)/(C_пред - C_исх) =

= erfc[х/(2)] - {е^α2Dτ+aх × [erfc (х/(2) +a)]}      (19)

где a = β/D  см^-1 относительный коэффициент передачи.

При β → ∞ уравнение (19) переходит в уравнение (3).

Решение уравнения (19) может быть представлено в безразмерном виде через критерий Био  Bi = α × x и критерий Тихонова Ti

Ti = a = Bi;  Q_{(x,τ )}= erfc (Bi/2Ti) - е^Tiα+ Bi × erfc [(Bi/2Ti) + Ti]         (20)

На поверхности изделий, т.е. при x = 0

Q_пов = Q_0,τ = 1 - е ^Ti2 × erfc (Ti)                                   (21)

Концентрация углерода С определяется только критерием Тихонова – соотношением между коэффициентами передачи и диффузии. Коэффициент, характеризующий скорость взаимодействия атмосферы с металлом, практически не зависит от температуры (лимитирует не скорость химических реакций, а скорость подвода в отвода реагирующих веществ), но зависит от линейной скорости W (м/с) омывающего потока газа. При W > 0,2 м/с

β’ = [0,25+0,63(W-0,2)^0,66] × 10^-6   г/см² × с × %С             (22)

При  увеличении скорости движения газа в печи от 0,2 до 3,2 м/с β’ растет от 0,25×10^-6 до 1,56 ×10^-6 г/см² × с ×%С. В практике газовой цементации стали скорость движения газа в печах обычно 1,3–1,5 м/с.

Распределение углерода по сечению диффузионной фазы находили решением уравнения (2). Оно привело к выражению (19) при следующих условиях:

1) глубина образующегося диффузионного слоя значительно меньше половины толщины детали (диффузия в полубесконечное пространство);

2) коэффициент диффузии D не зависит  от концентрации углерода;

3) скорость подачи углерода к поверхности зависит от состава поверхностного слоя металла, углеродного потенциала атмосферы в скорости движения потока

Q_пов = f(τ) = 1 –[ e^Ti × erfc (Ti)]

С учетом приведенных выше ограничений, полная математическая модель процесса газовой цементации выражается следующей системой дифференциальных уравнений

   при τ > 0, х > 0;                     (23)

С(х,0)=С₀  при х ≥ 0;                                       (24)

   при τ > 0;                   (25)

C_(∞,τ) = С₀ ;     = 0,

где С – концентрация углерода, % (по массе);

С₀  – начальная концентрация углерода в стали, % (по массе);

С_атм – углеродный потенциал атмосферы, % С;

τ – время, с;

D – коэффициент диффузии углерода в аустените, см²/с;

х – координата в направлении, перпендикулярном поверхности, см;

β – коэффициент перехода углерода из газа в металл, см/с;

(23) – дифференциальное уравнение нестационарной массопроводности (2-й закон Фика), описывает изменение распределения углерода в диффузионном слое;

(24) – начальное условие – это функция распределения углерода в стали при t = 0. Обычно C_о = const – начальное содержание углерода в стали;

(25) – граничное условие II рода, выражающее закон взаимодействия атмосферы с поверхностью металла.

Решение уравнения (19), системы уравнений (23–25) позволяет рассчитать процесс цементации, т.е. решить две задачи:

а) определить распределение углерода в слое по известным технологическим параметрам процесса (температура, время, состав атмосферы) и известным константам (коэффициент диффузии и коэффициент перехода углерода);

б) моделирование процесса газовой цементации подобрать технологические параметры процесса (температуру, время, состав атмосферы) для получения заданного профиля распределения углерода в слое по известным константам (D и β).

При этих условиях отпадает необходимость численного интегрирования уравнения (2) и задача решается на ЭВМ путем последовательного расчета аналитического выражения (20). Из рассчитанной в уравнении (20) безразмерной концентрации Q_(x,τ) можно легко найти концентрацию  С_(х,τ)

С(х,τ) = Q_(x,τ) × [C_пред- C_исх] + C_исх,                                               (26)

где C_исх – исходная концентрация углерода в стали (С_исх = C₀);

C_пред – максимально возможная при данных условиях насыщения концентрация, равная углеродному потенциалу атмосферы C_пред = C_атм.

Предложенная программа рассчитывает концентрационный профиль углерода (концентрацию на различном удалении от поверхности) в последовательные моменты времени. Для каждого варианта вводятся данные – температура t °C, начальная концентрация C₀, углеродный потенциал атмосферы C_атм, скорость газового потока W. Для каждого момента времени τ и координаты х вычисляются:

значения критериев Bi и Ti.   Bi = β’(х/D);     Ti = β’;

значения функций    erfc (Bi/2 Ti)   и    erfc  [(Bi/2 Ti) + Ti],

а затем значения Q по (20) и С_(х,τ) пo (26). Для каждого момента времени τ = 1...10 ч значения концентрации рассчитываются на расстояниях от поверхности х = 0...0,21 см c шагом х = 0,03 см.

Для понимания алгоритма вычисления функции необходимо заметить следующее. В функцию erfc (u) входит интеграл, зависящий от верхнего предела

erfc (u) = 1 - 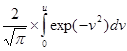                                     (27)

На каждом шаге расчета необходимо численное интегрирование функции exp (-v²). Эта процедура будет занимать основное время ее можно избежать, заменяя непосредственное интегрирование расчетом какой-либо аппроксимирующей функции, дающей с достаточной точностью значение интеграла. В настоящей работе используется одна из таких аппроксимаций

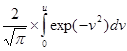 =  1-(а₁Z+ а₂Z²+ а₃Z³+ а₄Z⁴+ а₅Z⁵)е^-u2,                (28)

где   Z = 1/(1+а_n × u).

Константы  а₀ – а₅  равны: а₀  = 0,3276; а₁ = 0,2548; а₂ = -0,2845; а₃ = 1,4214; а₄ = -1,4532; а₅ = 1,0614.

Эта аппроксимация обеспечивает точность вычисления интеграла (см. формулу (28))  Δ = 1,5×10^-7. Обозначим выражение, стоящее в правой части равенства (28) в круглых скобках, через φ(u), тогда из части равенства (27) следует

erfc (u) = 1- [1-φ (u) × e ^-u2] = φ(u) × e ^-u2.                       (29)

Подставив (29) в (20), получим

Q_(x,τ) = φ  - 

и после преобразований получим (30)

Q_(x,τ) = .                                     (30)

Именно выражение (30) и рассчитывается в программе.

Образцы после цементации при 950° С закаливались после подстуживания до 850° C в воде. Твердость образцов после термообработки замеряли на приборе Роквелла по шкале НRC_э. Рассчитывали на ЭВМ по разработанной программе CEMENTIR концентрацию углерода в зависимости от расстояния от поверхности и времени  цементации С(_х,τ). Строили зависимости глубины цементованного слоя от параметров проведения процесса. За глубину слоя принимали слой с содержанием более 0,4% С.

Данные расчета и эксперимента о влиянии различных факторов на процесс газовой цементации стали отличаются не более чем на 7–10%.