Моделирование рецептур экструдатов методами математической статистики

Modeling of extrudate formulations using mathematical statistics

Ilya Sirokorensky

student, branch of the Federal State Institution of Higher Education "National Research University" MEI "in Smolensk, Russia, Smolensk

Аннотация. В статье рассмотрен классический подход к моделированию рецептур экструдатов. Для реализации методики используются пакеты Excel и MathCAD. Приведены аналитические выкладки, свидетельствующие о работоспособности методики.

Abstract. The classical approach to the modeling of extrudate formulations is considered in the article. To implement the methodology, Excel and MathCAD packages are used. Analytical calculations are given, which testify to the efficiency of the method.

Ключевые слова: математическое моделирование, математическая статистика, уравнение регрессии, рецептура экструдатов, снеки.

Keywords: mathematical modeling, mathematical statistics, regression equation, compounding of extrudates, snacks.

Рынок снеков в России в настоящее время является быстроразвивающимся и растущим. Одним из наиболее современных способов производства снеков является экструзия. Однако в условиях реального производства производителям экструдатов приходится сталкиваться с комплексом проблем при разработке рецептур, которые могут быть решены за счет построения математической модели разработки рецептур. Математическое моделирование может базироваться на минимальном количестве производственных испытаний, что ведет к снижению затрат [1].

Разработанная в статье математическая модель рецептуры экструдатов строится на классических методах математической статистики и базируется на эмпирических данных.

Построенная математическая модель, отражает зависимость удовлетворения органолептических потребностей (у) от рН среды экструдата (х₁), влажности экструдата (х₂) и содержания белка в экструдате (х₃). Построение системы показателей проводилось в пакете Exlel при помощи функции анализ данных. Статистические данные по переменным приведены в таблице 1.

Таблица 1.

Статистические данные математической модели

В результате анализа матрицы коэффициентов парной корреляции, приведенной в таблице 2,  следует, что зависимость удовлетворения органолептических потребностей от употребления экструдата имеет наиболее тесную связь с содержанием белка в рецептурной смеси, а влияние влажности и рН среды экструдата менее существенны. Взаимного влияния рассматриваемых факторов и слабых связей факторов не выявлено, что говорит о том, что все факторы учтены при построении математической модели.

Выполнив регрессионный и дисперсионный анализ  в пакете Excel, получили зависимости отраженные в таблице 3.

Таблица 2.

Корреляционная матрица

Уравнение регрессии зависимости удовлетворения органолептических потребностей от употребления экструдата от рН среды и влажности экструдата, содержания белка в рецептурной смеси, имеет вид:

У=-0,111-0,113Х₁-0,031Х₂+0,027Х₃

Таблица 3

Результаты регрессионного и дисперсионного анализа

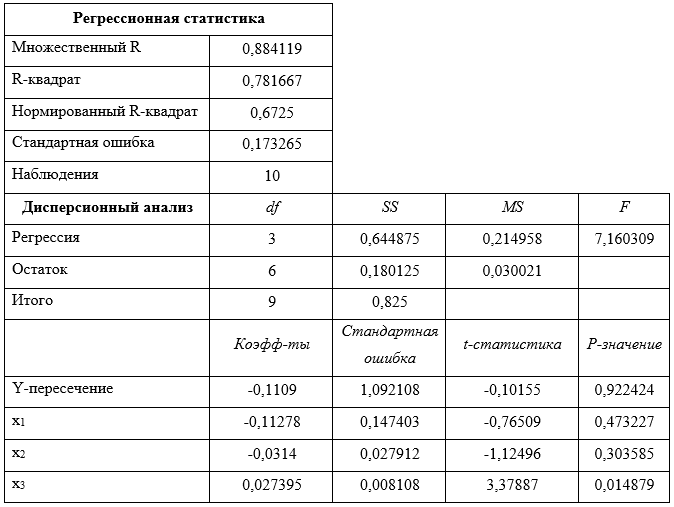
Вычисленное значение критерия Фишера для доверительной вероятности 95% и степеней свободы числителя и знаменателя 3 и 6 свидетельствует о неадекватности модели, поскольку расчетное значение не превышает табличное, равное 8,76.

Попытаемся привести модель к адекватному виду перейдя к нелинейной зависимости.

В первую очередь рассмотрим зависимости квадратичного вида. Наиболее значимыми переменными в модели являются влажность экструдата и содержание белка в рецептурной смеси. Составим уравнение регрессии при помощи пакета MatСАD.

Таким образом, новое уравнение регрессии имеет вид:

у=-0,018х₂²-0,04х₂-1,561·10^-3х₃²+0,147х₃+7,183·10^-3х₃х₂-4,79

Из рисунка 1 видно, что функция имеет экстремум.

Воспользовавшись критерием Сильвестра находим критические точки, обозначив через х –содержание белка в рецептурной смеси, а у – влажность экструдата, и представляя полученные уравнения для матричного метода в виде

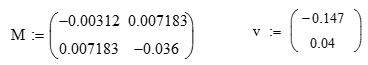
в МаtCAD, получим решение:

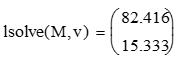
Рисунок 1. Функция зависимости удовлетворения органолептических потребностей от влажности экструдата и содержания белка в рецептурной смеси

Из полученного решения, можно сделать вывод о том, что максимальное удовлетворение органолептических потребностей от употребления экструдата будет достигаться при содержание белка в рецептурной смеси 82,4% и влажности экструдата 15% [2].