РЕАЛИЗАЦИЯ МЕТОДА СОПРЯЖЕННЫХ ГРАДИЕНТОВ НА ГРАФИЧЕСКОМ ПРОЦЕССОРЕ

Введение. В практических задачах часто возникает необходимость решения систем линейных алгебраических уравнений (СЛАУ) с симметричной, положительно определенной матрицей. Такие матрицы возникают, например, при дискретизации эллиптических уравнений математической физики и порождают линейные системы большой или очень большой размерности. В связи с этим при реализации алгоритмов решения СЛАУ на однопроцессорном компьютере могут возникнуть трудности из-за нехватки памяти, либо решение займет много времени. В этом случае необходимо использовать нестандартные подходы к написанию алгоритмов, основанные на использовании технологии параллельного программирования. Одним из методов решения СЛАУ является сведение исходной задачи к задаче безусловной минимизации квадратичной функции.

Целью данной работы является разработка параллельного алгоритма метода сопряженных градиентов для решения минимизации квадратичной функции. Для реализации поставленной цели была выбрана технология NVIDIA CUDA, как наиболее эффективное вычислительное средство, имеющая ряд преимуществ: доступность, легкость в изучении, поддержка практически любой современной видеокартой NVIDIA, наибольшая производительность.

Постановка задачи. Рассмотрим систему линейных уравнений (1) с симметричной, положительно определенной матрицей  размера :

                             (1)

Основой метода сопряженных градиентов является следующее свойство [1]: решение системы линейных уравнений (1) с симметричной положительно определенной матрицей  эквивалентно решению задачи минимизации функции:

                                          (2)

в пространстве . В самом деле, функция  достигает своего минимального значения тогда и только тогда, когда ее градиент равен нулю:

.

Таким образом, решение системы (1) можно искать как решение задачи безусловной минимизации функции (2).

Описание алгоритма метода сопряженных градиентов. Метод сопряженных градиентов для решения минимизации квадратичной функции (2) заключается в следующем [1]. На предварительном шаге задается начальное приближение , вычисляются начальный вектор невязки  и вектор направления :

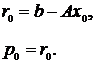
Дальнейшие приближения  определяются следующими формулами:

Здесь  — невязка -го приближения, коэффициент  соответству­ет выполнению условия сопряженности  направлений  и .

С этой точки зрения коэффициент  является решением задачи минимизации функции  по направлению :

.

Для нахождения точного решения системы линейных уравнений с положительно определенной симметричной матрицей необходимо выполнить не более  итераций. Однако, учитывая ошибки округления, данный процесс обычно рассматривают как итерационный. Вычисления завершаются при выполнении условия остановки:

,

где:  — приближение, полученное на итерации с номером ,  — приближение, полученное на предыдущей итерации. Параметр точности метода  задает исследователь. Также используется остановка при выполнении условия малости относительной нормы невязки:

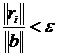.                                                       (3)

Организация параллельных вычислений. В методе сопряженных градиентов наиболее целесообразный подход для распараллеливания состоит в распараллеливании вычислений, реализуемых в ходе выполнения итераций.

Проведя анализ последовательного алгоритма метода сопряженных градиентов (рисунок 1), можно заключить, что основные вычислительные затраты приходятся на умножение матрицы  на вектора  и  (MultMatVec — 96,33 %). Поэтому для повышения эффективности работы метода достаточно распараллелить данную операцию. При реализации параллельных вычислений был использован параллельный алгоритм умножения матрицы на вектор, предложенный в учебном пособии [2, с. 78—81].

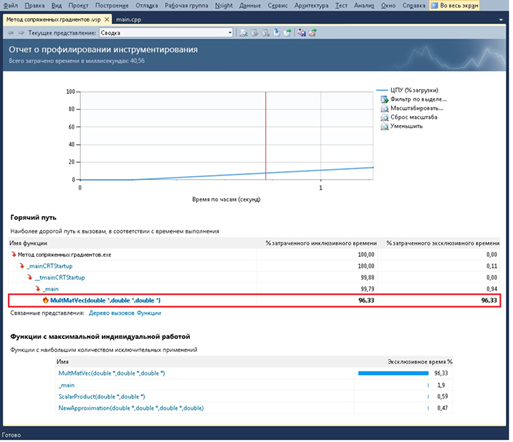
Рисунок 1. Анализ производительности алгоритма метода сопряженных градиентов

Также в алгоритме присутствуют различные операции над векторами, такие как: скалярное произведение, сложение и вычитание, умножение вектора на число. В распараллеливании данных вычислений нет необходимости, поскольку время, приходящее на обработку векторов незначительно, что следует из анализа (рисунок 1).

Рассмотрим более подробно схему распараллеливания операции умножения матрицы на вектор. Остальные же вычисления будут производиться на центральном процессоре (ЦПУ), т. е. последовательно.

В последовательной реализации операция умножения матрицы  на вектор  выглядит следующим образом (рисунок 2):

Рисунок 2. Умножение матрицы на вектор в последовательном исполнении

Приведем последовательный код умножения матрицы на вектор:

void MultMatVec(double *a, double *x, double *y)

{

for (int i=0; i<n; i++)

{

      double s=0;

      for (int j=0; j<n; j++)

          s+=a[i*n+j]*x[j];

      y[i]=s;

}

}

Вызов функции из основной программы осуществляется следующим образом:

...

MultMatVec(a,x,y);

...

В случае же использования параллельного программирования программный код можно преобразовать так, чтобы каждый шаг выполнялся параллельно остальным, а именно: каждая нить вычисляла бы единственное значение  — произведение строки  и вектора . Вычисления полностью независимы (рисунок 3).

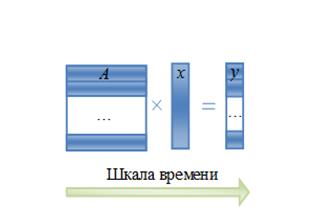
Рисунок 3. Умножение матрицы на вектор в параллельном исполнении

Чтобы функция выполнялась не процессором, а графическим устройством (ГПУ), они имеют квалификатор __global__.

Объявление функции ядра, осуществляющего алгоритм умножения матрицы на вектор, имеет следующий вид:

__global__ void kernelMultMatVec (double *a, double *x, double *y, int size)

{

int index = threadIdx.x + blockIdx.x * blockDim.x;

double s = 0;

for(int i = 0; i < size; i ++)

      s += a[index * size + i] * x[i];

y[index] = s;

}

Вызов ядра из основной программы осуществляется следующим образом:

kernelMultMatVec<<<BLOCKS, THREADS_PER_BLOCK>>>(dev_a, dev_x, dev_b, n);

Для работы с устройством использовались следующие встроенные функции:

·     выделение памяти на устройстве:

cudaMalloc((void **)&dev_a, n * n * sizeof(double));

cudaMalloc((void **)&dev_x, n * sizeof(double));

cudaMalloc((void **)&dev_y, n * sizeof(double)).

·     пересылка данных с ЦПУ на ГПУ:

cudaMemcpy(dev_a, a, size, cudaMemcpyHostToDevice);

cudaMemcpy(dev_x, x, size, cudaMemcpyHostToDevice).

·     пересылка данных с ГПУ на ЦПУ:

cudaMemcpy(y, dev_y, size, cudaMemcpyDeviceToHost).

Тестирование и анализ эффективности алгоритма. Для сравнения последовательной и параллельной реализаций алгоритма метода сопряженных градиентов была проведена серия экспериментов. Тестирование параллельного алгоритма проводилось на вычислительном кластере с центральным процессором Intel Xeon, 48Гб ОЗУ, с 3 графическими сопроцессорами NVIDIA TESLA C2075, а так же графическим процессором NVIDIA Quadro 2000.

Для проверки корректности реализованных алгоритмов использованы СЛАУ с известными точными решениями. Матрица  генерировалась следующим образом:

,

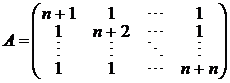где:  — размерность матрицы. В качестве вектора свободных членов  был взят вектор, полученный в результате перемножения матрицы  на вектор , где:  — точное решение СЛАУ (1). Вектор решения  заполняется случайными числами от  до . В качестве критерия останова взято условие завершения (3), точность метода .

Эффективность параллельных вычислений оценивается с помощью ускорения:

,

где:  — время решения задачи на однопроцессорном компьютере,  — аналогичное время при решении с использованием параллельного программирования. Подчеркнем, что под ускорением в данном случае понимается повышение производительности вычислений при использовании графического процессора относительно производительности вычислений, производимых на однопроцессорном компьютере.

В таблице 1 приведено время работы алгоритмов и полученное ускорение в зависимости от размера матриц. Следует отметить, что время работы алгоритма на графическом процессоре включает время, затрачиваемое на выделение памяти и копирование данных.

Таблица 1.

Сравнительный анализ параллельного и последовательного алгоритмов

Для иллюстрации приведенных данных в таблице 1 на рисунке 4 приведен график зависимости времени работы алгоритма на однопроцессорном компьютере и с применением технологии CUDA от размерности , на рисунке 5 представлен график ускорения  алгоритма от размерности .

Рисунок 4. Время работы последовательного и параллельного алгоритмов метода сопряженных градиентов

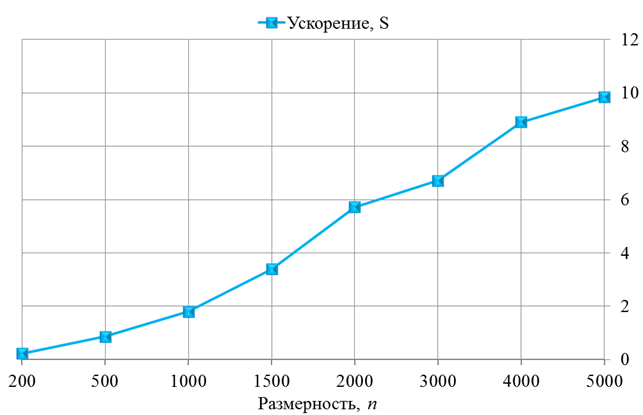
Рисунок 5. Ускорение алгоритма метода сопряженных градиентов

На графике, изображенном на рисунке 5, видно, что при небольшой размерности  (до 500) ускорение меньше единицы, то есть параллельный алгоритм работает медленнее, чем последовательный. Это связано с затратами времени на выделение памяти на графическом процессоре и последующим копированием в нее исходных данных.

На больших же размерах матрицы алгоритм эффективен, так как ускорение больше единицы. Из графика (рисунок 5) видно, что ускорение увеличивается с ростом числа .

Сравнительный анализ времени параллельного и последовательного алгоритмов метода сопряженных градиентов, показал, что применение технологии CUDA сокращает время решения задачи (до 10 раз). Однако следует отметить, что не имеет смысла использовать CUDA для работы с небольшими объемами данных. Для малых объемов входных данных ускорения практически не наблюдалось.

Список литературы:
1.    Баркалов К.А. Методы параллельных вычислений. Н. Новгород: Изд-во Нижегородского госуниверситета им. Н.И. Лобачевского, 2011 — 124 с.
2.    Варыгина М.П. Основы программирования в CUDA. Учебное пособие. Красноярск: Краснояр. гос. пед. ун-т им. В.П. Астафьева, 2012 — 138 с.
3.    Гергель В.П. Высокопроизводительные вычисления для многоядерных многопроцессорных систем. Учебное пособие. Н. Новгород: Изд-во ННГУ им. Н.И. Лобачевского, 2010. — 421 с.
4.    Сандерс Д., Кэндрот Э. Технология CUDA в примерах: введение в программирование графических процессоров. / под ред. ДМК Пресс. Пер. с англ., 2011. — 232 с.