Напряженное состояние кирпичного свода с вырезанным проемом

Введение

При реконструкции исторических зданий часто возникает необходимость тем или иным образом переоборудовать их под современные требования. Такое переоборудование, как правило, включает в себя использование современных материалов, изменение конструкции отдельных элементов здания и установку новых систем – вентиляции, водоснабжения и других. Уже имеющихся в здании технологических проемов часто бывает недостаточно для установки этих систем и требуется устройство новых. Все это влечет за собой существенное изменение напряженного состояния элементов здания и их расчетной схемы [2]. Так как исторические здания построены главным образом из каменной и кирпичной кладки, ее расчет и составляет основную сложность, в особенности – расчет кирпичных сводчатых перекрытий.

Моделирование каменных сводов представляет собой сложную задачу [1]. Проведенный анализ публикаций [3] демонстрирует почти полное отсутствие российских работ, посвященных этой тематике. Зарубежные исследования можно условно разделить на две группы: поиск методов численного моделирования, позволяющих наиболее точно отразить работу сводов различной конфигурации [6; 7] и экспериментальное изучение механизмов разрушения кирпичных арок и сводов [4; 5]. Исследования подробно описывают причины разрушения сводов, потери ими устойчивости и механизмы таких процессов. Однако стоит отметить, что в этих работах рассматриваются обычные, не модифицированные арки и своды. В то время как поведение сводов с различными дополнительными проемами и пути перераспределения напряжений в них представляет большой практический интерес.

Авторами был испытан свод реконструируемого корпуса «Кузница» в комплексе Новая Голландия в Санкт-Петербурге. В процессе реконструкции возникла необходимость крупного проема в одном из сводов для вывода систем вентиляции. После вырезания проема, в процессе раскружаливания свода были измерены деформации на примыкающих участках. Также свод был смоделирован в программном комплексе ABAQUS для оценки его напряженного состояния. Результаты испытаний и численного анализа представлены в данной статье.

Постановка задачи и исходные данные

Для изучения влияния проема на напряженно-деформированное состояние свода было необходимо решить следующие основные задачи:

·     Измерить деформации на прилегающих к проему участках реального свода.

·     Смоделировать свод в ПК ABAQUS и произвести расчет.

·     Сравнить результаты измерений с данными численного моделирования.

В своде корпуса «Кузница» был вырезан проем с габаритами 88x422 см. Для его устройства на значительном участке была удалена старая кладка и выложена новая. Свод – цилиндрический, с дугой переменного радиуса и усилением сечения у пят (рис. 1). Основные характеристики кладки свода: объемная масса γ=1800 кг/м³, модуль упругости E=1680 МПа, коэффициент Пуассона μ=0.2.

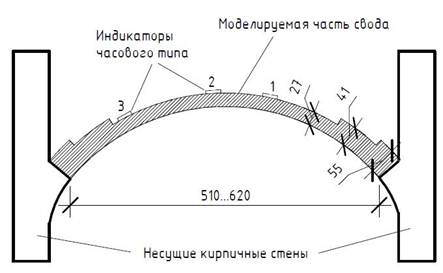
Рисунок 1. Конструктивная схема свода и расположение индикаторов, размеры даны в см

Точность индикаторов (рис. 2) составляет 0.001 мм. По результатам измерений были определены перемещения: на первом участке -0.007 мм, на втором -0.004 мм, на третьем -0.013 мм. Показания третьего индикатора позволяют сделать вывод о том, что кладка переложенного участка (индикаторы 1 и 2) является более жесткой. Соответствующие относительные деформации для базы прибора 20 см: на первом участке 3.5∙10^-5; на втором 2∙10^-5; на третьем 6.5∙10^-5. Для принятого модуля упругости кладки 1680 МПа главные сжимающие напряжения на этих участках составят: 58.8 кПа, 33.6 кПа и 109.2 кПа соответственно.

Рисунок 2. Индикатор часового типа для измерения деформаций свода

Моделирование свода

По конструкции свода предполагалось, что опорная вертикальная реакция и горизонтальный распор от собственного веса сводов передается его пятами непосредственно на фундамент по оси стены. В этом случае можно получить наиболее точные результаты расчета, если обрезать моделируемый свод перпендикулярно его сечению в точке примыкания пяты к несущей стене.

Расчетная пространственная схема свода генерировалась объемными конечными элементами. Соединение распалубок со сводом принималось жестким. Передача вертикальных и горизонтальных реакций козырьками распалубок на примыкающие к ним стены исключалась. Предполагалось также, что свод не опирается на смежные с ним кирпичные поперечные стены. Расчеты выполнены только от собственного веса каменной кладки свода с коэффициентом перегрузки 1.1. В расчете не учитывалась забутовка над пятами свода ввиду незначительного ее влияния на рассматриваемую зону.

Свод был смоделирован в 2 вариантах – исходное состояние и с вырезанием существующего проема.

Рассматриваемый свод в обычном состоянии имеет критические зоны в характерных местах: небольшие растягивающие напряжения в шелыгах распалубок и концентрация сжимающих напряжений у их оснований, а также концентрация напряжений в зоне перепада сечения кладки (рис. 3).

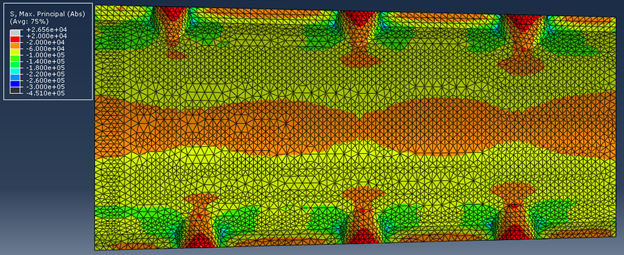
Рисунок 3. Максимальные главные напряжения на внутренней поверхности свода, Па

После врезания проема возникли критические участки на границе проема (рис. 4). У торца проема возникли опасные растягивающие напряжения, действующие перпендикулярно основному потоку сжимающих напряжений. В то же время распалубка, примыкающая к проему, наоборот оказалась частично разгруженной, исчезли растягивающие напряжения в шелыге, а величина сжимающих напряжений у её основания уменьшилась.

Рисунок 4. Максимальные главные напряжения в зоне проема с внутренней стороны свода, Па

На участках, соответствующих участкам замеров в реальном своде, сжимающие напряжения составили: 1 – (0.07…0.08 МПа), 2 – (0.08…0.09 МПа), 3 – (0.11…0.12 МПа). Таким образом, численно напряжения в старой кладке практически полностью совпадают с напряжениями в расчетной модели. Несоответствие расчетных напряжений в новой кладке напряжениям в модели предположительно вызвано большей жесткостью кладки этого участка.

Выводы

1.  Из анализа траекторий максимальных главных напряжений можно сделать вывод о том, что ослабление сечения предпочтительнее производить параллельно линиям действия главных напряжений. В то же время, ослабление сечения свода в направлении, перпендикулярном этим линиям, вызывает появление опасных растягивающих напряжений.

2.  Сопоставление результатов численного моделирования с данными испытаний показало допустимость использования сплошной модели свода в численном анализе. Расхождение результатов на участке новой кладке вызвано ее большей жесткостью, так как при моделировании для всего свода были заданы характеристики старой кладки.

3.  В условиях малой изученности поведения кладки сводов, а также разнообразия их конструктивных вариантов, испытания, аналогичные рассмотренным в статье, полезны и необходимы для корректировки и анализа результатов численного моделирования сводов.