Атака Padding Oracle на блочные шифры
Секция: Технические науки

XL Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
Атака Padding Oracle на блочные шифры
В данной статье рассматривается атака Padding Oracle, применяемая для раскрытия исходного текста без знания ключа, используя лишь особенности режима сцепления блоков CBC и правило дополнения сообщения.
Блочные шифры
Суть блочных шифров заключается в разбиении исходного сообщения на блоки одинаковой длины N, дополнении (padding) последнего блока определенными байтами до длины N и последующего шифрования каждого блока.
Стандартом PKCS#7 предусмотрено следующее правило дополнения блока: если размер блока равен N, а число занятых байт в последнем блоке равно L, то в конец данного блока дописываются N – L байт со значением N – L. Например, если N = 8, а L = 5, то в конец блока допишутся 3 байта со значением 03, так как N – L = 3.
В работе рассмотрен определенный режим сцепления блоков: Cipher Block Chaining (CBC). Схема CBC выглядит следующим образом:

Рисунок 1. Схема шифрования в режиме CBC

Рисунок 2. Схема расшифровки в режиме CBC
Здесь Pi – блоки исходного сообщения, Ci – зашифрованные блоки, К – ключ шифрования, EK – функция шифрования, DK – функция расшифровки, IV – инициализирующий вектор, «+» – операция XOR. IV представляет собой некоторую известную строку байт с длиной, равной длине блока.
Padding Oracle
При атаке Padding Oracle предполагается, что мы можем отправлять сообщения некоторому приложению (Оракулу) на расшифровку, которое может возвращать ответ, корректно ли выполнено дополнение последнего блока. Расшифровка сообщения происходит с последних блоков шифротекста. Рассмотрим алгоритм расшифровки блока Ci+1.
1. Сформируем блок R, все байты которого, кроме последнего, зададим случайными значениями. Перебираем байт RN от 0x00 до 0xFF, каждый раз посылая Оракулу сообщение [R||Ci+1] для расшифровки, где «||» означает конкатенацию блоков. Если при некотором значении RN Оракул «одобрит» дополнение, то мы можем утверждать, что дополнение при расшифровке получилось равным 01 (TN = 01). После этого вычисляем SN = RN xor 0x01. SN является последним байтом блока так называемого «промежуточного состояния». Найдя SN, мы можем вычислить pN = SN xor cN.

Рисунок 3. Пояснение к первому шагу атаки
2. Сформируем новый блок R, все байты которого, кроме двух последних, зададим случайными значениями. RN = SN xor 0x02, чтобы всегда получать TN = 02. Перебираем байт RN-1 от 0x00 до 0xFF, каждый раз посылая Оракулу сообщение [R||Ci+1] для расшифровки. Если при некотором значении RN-1 Оракул «одобрит» дополнение, то мы можем утверждать, что дополнение при расшифровке получилось равным 02 02 (TN-1 = 02). После этого вычисляем SN-1 = RN-1 xor 0x02. Блок Ii+1 остается неизменным во время расшифровки блока Ci+1. Найдя SN-1, мы можем вычислить pN-1 = SN-1 xor cN-1.

Рисунок 4. Пояснение ко второму шагу атаки
На третьем шаге соответственно пытаемся получить дополнение 03 03 03, на четвертом – 04 04 04 04 и так далее. После N шагов получаем полностью блок Pi+1. Далее переходим к блоку Ci и находим блок Pi, отбрасывая при этом блок Ci+1 из рассмотрения, считая блок Ci последним. При расшифровке блока С1 в качестве предыдущего блока берем IV.
Рассмотрим пример расшифровки сообщения C, которое разбивается на блоки C1 = [8b1e394e9c3a37c8073fb0e300a3b479] и C2 = [4e890457a0b83dd105bb76b8723203a9].
Каждая строка на рисунках 5 и 6 – один шаг. Зеленым цветом выделен блок R, «##»– случайный байт. Красным цветом выделен блок I, «##» –неизвестный на данном шаге байт. Желтым цветом выделен блок P, «#» – неизвестный на данном шаге байт. Нераспознанные символы на рисунке 5 – это байты 06 06 06 06 06 06, которыми дополнялся последний блок перед шифрованием сообщения.
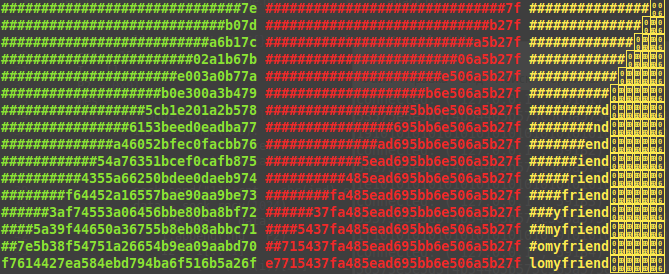
Рисунок 5. Расшифровка блока C2

Рисунок 5. Расшифровка блока C1
Заключение
В данной статье рассмотрен алгоритм атаки Padding Oracle, который использует уязвимости дополнения блока и режима сцепления блоков CBC. Рассмотрен пример, показывающий эффективность данной атаки.





