Прогнозирование числа оставшихся ошибок программного обеспечения при отладке на основе гипотезы Джелинского-Моранды

В работе будет рассмотрен способ достижения ПО необходимой надежности в процессе отладки и эксплуатации, если число проявившихся ошибок, как и время их обнаружения, известно.

Введение

Одним из этапов разработки программного обеспечения является отладка программы, в котором обнаруживают, локализуют и устраняют ошибки. Было бы достаточно удобно иметь модель прогнозирования надежности программного обеспечения для оценивания времени, необходимого на отладку.

ПО, часто достаточно сложное, разрабатывается различными людьми, каждый из которых отвечает за свою часть и имеет индивидуальную частоту появления ошибок. Если допустить в модели надежности наличие свободных параметров, то эти препятствия можно преодолеть.

Краткие теоретические сведения

Модель ошибок в программном обеспечении Джелинского-Моранды гласит: ошибки ПО появляются тем чаще, чем их больше. И наоборот, чем более отлажено программное обеспечение, тем реже частота их появления.

Математическая формулировка

l – интенсивность проявления ошибок (средняя),

N₀ – начальное количество ошибок,

n – количество обнаруженных ошибок,

k – коэффициент пропорциональности, K> 0,

Dn_i – приращение количества обнаруженных ошибок на интервале Dt. В уравнении два неизвестных N₀ и k.

Уравнение для нахождения коэффициента пропорциональности k

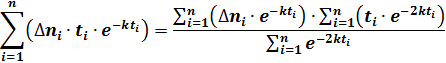
Экспериментальная часть

Нами была разработана программа для определения среднего числа начального количества ошибок и среднего числа оставшихся ошибок в ПО по модели Джелинского-Моранды методом наименьших квадратов (МНК) по наблюдениям за числом проявившихся в процессе отладки ошибок и времени их обнаружения.

Проведем эксперимент. Предположим, что в течение недели производилась отладка программного обеспечения. В первый день было обнаружено 5 ошибок, во второй – 3, в третий день – 1 и в четвертый ещё 2. В следующие три дня ошибки обнаружены не были.

Определим параметры модели N₀ и К численной процедурой.

Рисунок 1. Определение параметров модели

Получаем K = 0.3471, N₀ = 21.6309.

Рисунок 2. Определение расчетных значений экспоненциальной аппроксимации

Начальное количество ошибок: 21. На момент времени t = 7 ошибок осталось: 21.69 – 5.33 – 3.76 – 2.65 – 1.87 – 1.32 – 0.93 – 0.65 = 5.12.

Т.к. нулевому количеству оставшихся ошибок в ПО, по условию, соответствует значение 0.0001, по данной модели отладка закончится через 29 дней. То есть через 29 дней от начала отладки вероятность отсутствия ошибок будет больше 0,999.

Построим график изменения числа обнаруженных ошибок во времени по модели надежности ПО Джелинского-Моранды (рисунок 3).

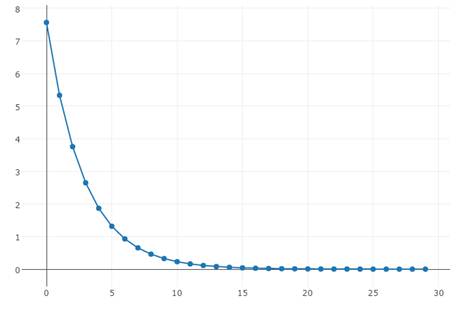
Рисунок 3. График изменения числа обнаруженных ошибок во времени

Применим линейную аппроксимацию к исходным данными.

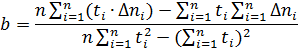
Расчет коэффициентов  и :

b: 5.14, a: -0.71

Рисунок 4. Определение расчетных значений линейной аппроксимации

Найдены начальное число ошибок N0 ≈ 21.6228 и коэффициент пропорциональности k ≈ 0.3498 с точностью ε = 0,0001.

На основе расчетов в ПО осталось ≈ 5 ошибок.

Сумма невязок равна -0,0000 для линейной интерполяции (для экспоненциальной -0,5000). Сумма квадратов невязок равна 3.14 для линейной интерполяции (для экспоненциальной 4.46).

В отличие от экспоненциального метода решения, на графике расчетных значений линейной интерполяции имеются отрицательные значения числа найденных ошибок, что делает невозможным прогноз после t=7.

Заключение

Мы рассмотрели возможный способ контроля отлаженности программного обеспечения в процессе отладки. Была разработана соответствующая программа, которая позволяет определить среднее число начального количества ошибок и среднее число оставшихся ошибок в программном обеспечении, а также прогнозируемое время завершения отладки программного обеспечения.