Построение и решение геометрических моделей

Линия «Моделирование и формализация» появилась в программе обязательного минимума ФГОС ООО второго поколения недавно, поэтому она находится в процессе активного изучения и рассмотрения. Чтобы разработать методику изучения содержательной линии «Моделирование и формализация» требуется проявить творческие способности и использовать инновационный подход. Совокупность понятий из темы представляет аналитический инструмент, который совершенствует мировоззренческие взгляды на мир как на информационную систему. Разработка процессов моделирования вносит новизну в рассмотрении информации и культуры, так же формирует компетенции учащихся в сфере исследования рынка профессий и её выбора. С целью рассмотрения привычных путей исследования естественнонаучных дисциплин, необходимо научиться использовать персональный компьютер как инструмент учебной деятельности. Данный подход к использованию компьютера поможет также увеличить экспериментально-исследовательские способности учащихся, что поможет активизировать процесс познания в реальном времени [2, с 45].

При изучении содержательной линии «Моделирование и формализация» можно использовать цифровые образовательные ресурсы на портале Единой коллекции цифровых образовательных ресурсов. Они могут быть использованы на уроках учителем и учащимися при самостоятельном изучении темы.

Рассмотренный способ изучения линии «Моделирование и формализация» способствует развитию мотивации к более подробному и активному изучению этой линии, расширяется кругозор и познавательная деятельность, это приводит к прогнозируемому улучшения качества сформированных знаний и умений по теме «Моделирование и формализация» [1, с 333].

Проанализировав школьные учебники таких авторов как, Н. Угринович, А. Г. Гейн и Н. В. Макарова, можно сделать следующий вывод. Данная темы, в учебниках и задачниках раскрыта не в полном объеме – нет классификации моделей (кроме учебника Н. В. Макаровой), перечислены не все из основных типов информационных моделей, существует путаница в определениях. Теоретический материал представлен не очень удачно, практически отсутствуют примеры. Не полностью показана важность данной темы, её прикладное применение, как на уроках информатики, так и на других уроках [3, с 45]. Практическая часть не вызывает особого интереса у учеников, не мотивирует их к изучению тем, и кроме того, затрагивает лишь часть упомянутых типов информационных моделей (либо вообще отсутствует). Задачи по моделированию сводятся к работе в MS Excel или к программированию в Visual BASIC. Нет заданий на определение типов информационных моделей, их ограничений.

В настоящее время трудно найти область человеческой деятельности, в которой не использовались бы компьютерные симуляции. Увеличение общей производительности вычислительных систем привело к тому, что компьютерные модели применяются для решения разнообразных задач, начиная от моделирования формы ногтей и причесок и заканчивая предсказанием погоды, расчетом комет и астероидов, прогнозом развития человеческой цивилизации. Поэтому целесообразно проводить элективные курсы и факультативные занятия для реализации линии «Моделирование и формализация», пополнить раздел трёхмерной графики задачами на разработку анимированных сцен (процессов и явлений, изучаемых в других предметах), с целью формирования прочных знаний, умений и навыков в области разработки анимации и внесения динамики в обучение другим предметным областям.

Например, рассмотрим задание 16 из ЕГЭ по математике (по планиметрии), решенное на ПК и мобильном устройстве с помощью среды GeoGebra.

В треугольнике ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD=R.

a)  Докажите, что треугольник ABC прямоугольный.

b)  Вписанная окружность касается сторон AB и BC в точках E и F. Найдите площадь треугольника BEF, если известно, что R=3 и CD=9.

Решение:

a)  Пусть O – центр вписанной окружности треугольника ABC. Центр окружности, вписанной в угол, лежит на его биссектрисе, значит, AO ­– биссектриса угла BAC (рис. 1, рис. 2).

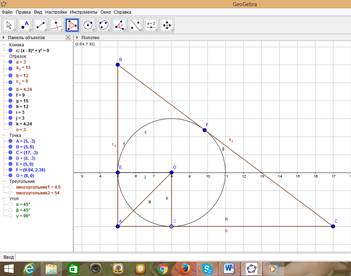
Рисунок 1. Вид полотна с условием задачи (GeoGebra)

Рисунок 2. Вид полотна с условием задачи (GeoGebra мобильная)

Треугольник AOD прямоугольный и равнобедренный, поэтому ∠OAD = 45°. Значит, ∠BAC = 90°, что и требовалось доказать (рис. 3, рис. 4).

Рисунок 3. Полотно результата (GeoGebra)

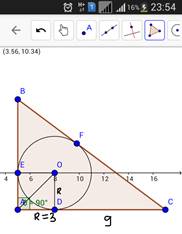
Рисунок 4. Полотно результата (GeoGebra мобильная)

b)  Обозначим BF=x. По теореме о равенстве отрезков касательных, проведённых к окружности из одной точки, AE = AD = 3, CF = CD = 9 и BE = BF = x. По теореме Пифагора , или . Из этого уравнения находим, что x=6. Тогда 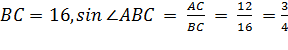 (рис. 5, рис. 6).

Следовательно,  .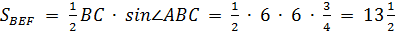

Ответ: 

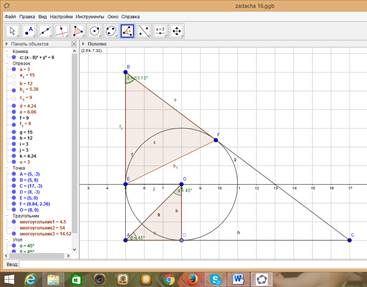
Рисунок 5. Полотно результата (GeoGebra)

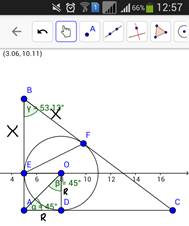
Рисунок 6. Полотно результата (GeoGebra мобильная)