Моделирование средствами символьной математики решения дробного интегрального уравнения прямыми методами

В статье средствами символьной математики моделируется решение дробного интегрального уравнения, экспериментально показывается сходимость приближенного решения к точному.

Пусть X и Y произвольные линейные нормированные пространства, а  и  (=1, 2, …) их произвольные линейные подпространства конечной размерности.

Рассмотрим уравнения

  (1.1)

  (1.2)

где:  и  – аддитивные и однородные операторы, действующие из  в и из  в  соответственно.

Уравнение (1.2) при любом фиксированном эквивалентно системе линейных алгебраических уравнений порядка  относительно коэффициентов разложения элемента  по базису пространства . Этим и можно объяснить причину замены нашего бесконечномерного уравнения (1.1) конечномерным уравнением (1.2).

Рассмотрим дробное интегральное уравнение с интегралом Вейля:

,

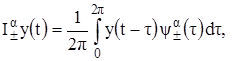
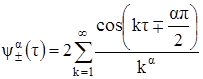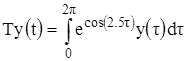где: , дробный интеграл Вейля определяется из определения: . Оператор - вполне непрерывен и действует на функцию  следующим образом: . Подставляя в это уравнение значения  получим следующее уравнение:

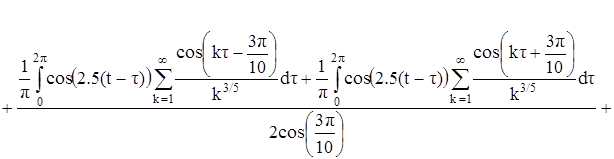
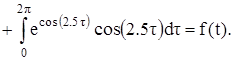
Найдем для этого уравнения значение . Проводя необходимые вычисления, получим:

.

Далее решим исходное уравнение методом Бубнова – Галеркина. Приближенное значение будем искать в виде полинома 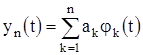. Функции  являются базисными функциями и имеют вид .

Подставляем приближенное значение  в исходное уравнение:

,

Неизвестные коэффициенты  определим из условий

,

где 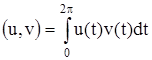. Получаем СЛАУ n порядка относительно :

.

Решим эту систему для n=3:

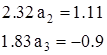
Получим:  и .

Близость приближенного решения к точному можно оценить по изображению на графике (см. рис.) и по таблице (см. табл.).

Рисунок 1.

Таблица 1.

Разница приближенного значения функции от точного в точках