Ряд Фурье в электротехнике

Жили Жозеф Фурье во времена Наполеона, который работал во Франции и Египте, Фурье предвосхитил идею расширения функции Р в серии тригонометрических функций и по-прежнему завораживают математический, физический, статистические и инженер. В начале 1800-х годов разработал свою серию для изучения распространения тепла и принимая во внимание, что самая простая форма, которая является синусоидальной функцией, которая показала, что любая функция более сложна она, она может быть разложена в виде суммы синусов и косинусов.

Ряд Фурье. Периодический функций  с периодам  определенной на отрезке , называем ряд

где:

Теорема Дирихле. Пусть функция  на отрезке  имеем конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва I рода.

Изображение несинусоидальных токов с помощью рядов Фурье. Периодическую функцию  с периодом , удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье.

Рассчитаем это электрический цепи c помощью рядов Фурье:

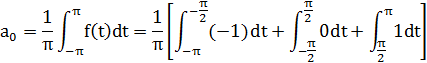
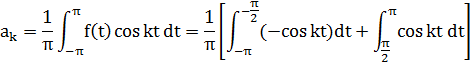
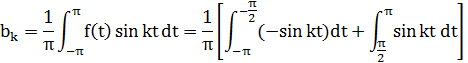
K=1, 2, 3, 4,……, n

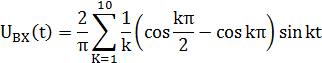
Выводы: в ряды Фурье любая произвольная функция можем записать в периодических бесконечных условиях. Можно видеть, что исследования Джозефа Фурье, сыграли важную роль в развитии математики в то время и по сей день есть несколько ученых и студентов из области физики и техники, чтобы использовать ресурсы, что ряд Фурье обеспечивают, чтобы банки применять и развивать свои исследования. Для того, чтобы войти в этот увлекательный мир, с дальнейшим изучением, легко понять эти вопросы, что эти функции реализованы в ряд Фурье взять нас. Таким образом, следует отметить, что любая функция может быть разложена в виде суммы синусов и косинусов, будучи очень полезным инструментом для представления периодических функций. Ряд Фурье имеет большое значение для практического применения в физике и технике, например, принудительный гармонический осциллятор, бесконечный пучок упругие наземный среди так много, поэтому крайне важно признать ту роль, которую ряды Фурье представляют для нас, и возможность изучить их, он становится еще более полезным.