Разработка программного комплекса для электронного учебного курса в LMS Blackboard

В данной работе представлены результаты разработки программного комплекса, который реализует интерактивное онлайн обучение методам математической статистики и позволяет проводить исследования этих методов с помощью современных информационных технологий.

Основные принципы создания и применения электронных образовательных ресурсов для E - learning

В настоящее время имеет место необходимость разработки электронных образовательных ресурсов, которые позволяют формировать профессиональные компетенции в процессе обучения.

Электронный образовательный ресурс (ЭОР) – образовательный ресурс, представленный в электронно-цифровой форме и включающий в себя структуру, предметное содержание и метаданные о них, где метаданные – структурированные данные, предназначенные для описания характеристик ЭОР.

Структура ЭОР может быть представлена в виде блоков учебного материала, представляющих собой совместно используемые объекты содержания:

·     текст;

·     графические иллюстрации;

·     элементы гипермедиа;

·     программы.

Все большее распространение в образовательном процессе имеет смешанная форма обучения – Blended Learning, – это особая организация обучения, которая позволяет совмещать обучение в аудитории и современные технологии обучения в электронной дистанционной среде. В качестве таких электронных дистанционных сред в настоящее время выступают LMS – Learning Management System – (англ. Система управления электронным обучением). Примером LMS может служить система дистанционного обучения Blackboard, являющаяся электронной средой КНИТУ-КАИ.

Благодаря смешанной форме обучения Blended Learning:

·     студент получает возможность обучаться в группе с преподавателем и дополнительно дома в удобное для него время;

·     студент сам устанавливает оптимальную скорость и интенсивность процесса обучения;

·     затраты на обучение при данном методе сокращаются в несколько раз;

·     данный метод дисциплинирует и помогает научиться работать самостоятельно.

Появление Интернета и Web-технологий дало форме обучения Blended Learning новые возможности развития.

В современном дистанционном и смешанном обучении используются разработанные электронные учебные курсы, учитывающие педагогические и психологические аспекты преподавания с использованием инновационных технологий, которые при данных типах обучения являются основным информационно несущим инструментом [1, с. 53].

Электронный учебный курс является основным структурным элементом при дистанционном и смешанном обучении, а также может служить хорошей поддержкой очного обучения, где всё больше и больше увеличивается доля самостоятельной работы студентов [2, с 979].

Таким образом, в настоящее время существует необходимость разработки интерактивных электронных образовательных ресурсов для электронных учебных курсов. Эта задача решается с учетом возможностей конкретных LMS. В данной работе предлагается универсальный подход к созданию интерактивных ЭОР на основе разработки интерактивных программ с использованием языка JavaScript. Данный подход является современной реализацией методов дидактического и программного проектирования информационных технологий обучения учебным дисциплинам, имеющим сложную логическую структуру, к которым относятся дисциплины по математике, в состав которых входят сложные математические методы. В связи с этим возникает необходимость разработки интерактивного программного обеспечения, позволяющего в режиме реального времени выполнять алгоритмы математических методов с возможностью изменять параметры алгоритма на различных его шагах с целью их изучения и исследования [3, с.74–76].

Необходимость изучения математических дисциплин с помощью информационных технологий обусловлена также и тем, что в условиях современной требований к выпускнику, выделяется задача формирования компетенции, предусматривающая умение решать математические задачи с использованием современных информационно-коммуникационных технологий. Формирование компетенций умения решать практические задачи в режиме онлайн в электронной среде возможно средствами некоторых LMS. Примером такой LMS является интеллектуальная система обучения математике Math-Bridge, в которой имеются встроенные средства для создания динамических учебных объектов (упражнений). Разработанные в системе Math-Bridge упражнения можно настроить на использование их в режиме электронного тренинга по решению практических математических задач или для контроля умений решать практические математические задачи [4, с. 526].

Обычные LMS таких встроенных средств не содержат. Как правило, разработка элементов интерактивных ЭОР в таких LMS возможна при создании тестовых заданий, которые в дальнейшем могут быть использованы только для формирования тестов и контроля знаний. Для решения задач в режиме тренинга встроенных средств в таких LMS нет. Например, система Blackboard позволяет создавать тестовые задания, содержащие интерактивные элементы. Примерами таких тестовых задания являются задания на соответствие, на упорядочение элементов, на конструирование, «горячая точка».

Алгоритмы построения статистических оценок функций и плотности распределения на языке JavaScript

Разработанный программный комплекс содержит алгоритмы построения и исследования статистических оценок функций и плотности распределения на языке JavaScript.

Для работы этих алгоритмов разработаны вспомогательные алгоритмы моделирования случайных величин в соответствии с заданным законом распределения (нормальный, равномерный, показательный), а также программы вывода динамических графиков.

Структурная схема алгоритма «Построение статистической оценки функции и плотности распределения» представлена на рис. 1.

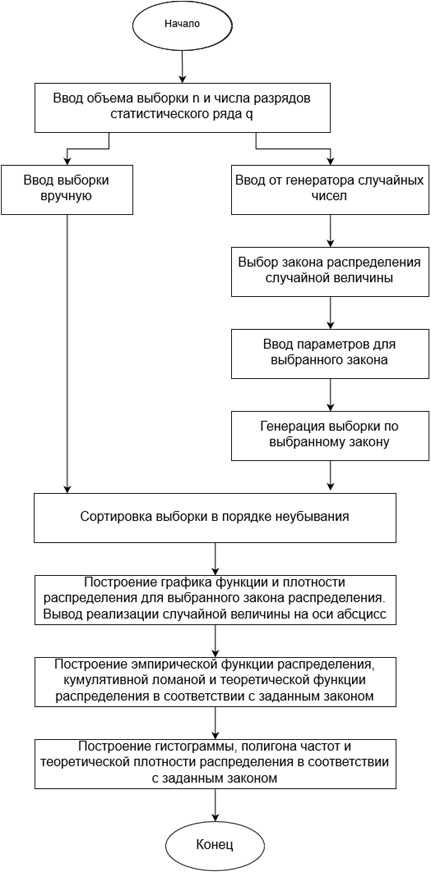
Рисунок 1. Алгоритм «Построение статистической оценки функции и плотности распределения»

Выполним описание работы алгоритма по шагам.

1)  Осуществляется формирование выборки. Пользователь может ввести вручную объём выборки в пределах от 5 до 1000.

2)  Пользователь вводит число разрядов в пределах от 5 до 25.

3)  Далее выбирается режим формирования выборки: пользователь должен выбрать закон распределения случайной величины, либо ввести данные вручную.

1.  Равномерный закон с параметрами a, b; где –100≤a≤100, a<b≤200;

2.  Показательный закон с параметром l, где 0<l≤10.

3.  Нормальный закон с параметрами m,s²; где –100≤m≤100, 0<s²≤10;

4.  Ручной ввод данных. Допускается ввод не более 100 чисел через пробел. В качестве десятичного разделителя используется точка.

4)  В соответствии с выбранным законом распределения и заданными параметрами будут сгенерированы выборочные данные и построены графики функции и плотности распределения. На оси абсцисс будут показаны сгенерированные значения реализации случайной величины.

5)  Следующим шагом является построение оценки функции распределения. На основе сгенерированной выборки будут построены графики эмпирической функции распределения F*(x) и кумулятивной ломаной F**(x). Для оценки точности методов на графике синим цветом представлена теоретическая функция распределения в соответствии с заданным законом.

6)  Следующим шагом является построение оценки плотности распределения. На основе сгенерированной выборки будут построены графики гистограммы f*(x) и полигона частот f**(x). Для оценки точности методов на графике красным цветом представлена теоретическая плотность распределения в соответствии с заданным законом.

Структурная схема алгоритма исследования статистических оценок функции и плотности распределения представлена на рис. 2.

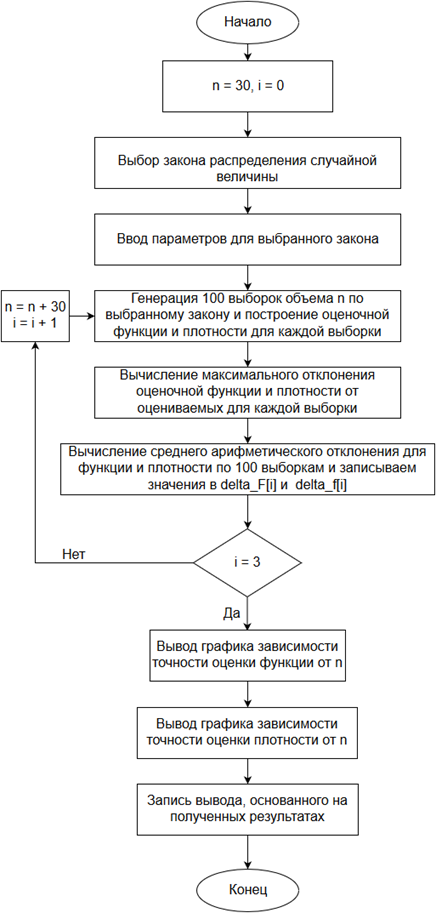
Рисунок 2. Алгоритм «Исследование статистических оценок функции и плотности распределения»

Рассмотрим выполнение алгоритма по шагам:

1)  Для исследования зависимости точности оценивания функции распределения от n – объема выборки программа выполняет 100 циклов построения оценки функции распределения для объема выборки n равной 30 и записывает максимальное отклонение каждой оценочной функции от оцениваемой. После чего программа вычисляет среднее арифметическое для полученных 100 отклонений. Аналогичные действия происходят для объема выборки n равной 60 и 90. Далее выводится график зависимости точности оценивания F(x) от n.

2)  Для исследования зависимости точности оценивания плотности распределения от n – объема выборки программа выполняет 100 циклов построения оценки плотности распределения для объема выборки n равной 30 и записывает максимальное отклонение каждой оценочной функции от оцениваемой. После чего программа вычисляет среднее арифметическое для полученных 100 отклонений. Аналогичные действия происходят для объема выборки n равной 60 и 90. Далее выводится график зависимости точности оценивания f(x) от n.

Выводятся следующие результаты исследования: были проведены исследование параметров функции распределения – F(x) и плотности распределения – f(x) от n – объёма выборки. При проведении исследований, было выявлено, что при увеличении объема выборки n точность методов возрастала. Об этом свидетельствует уменьшение среднего отклонения ΔF и Δf.

Программная реализация рассмотренных алгоритмов интегрировано в LMS Blackboard и позволяет обучить пользователя алгоритмам оценивания функции и плотности распределения по выборке измерений случайной величины, сгенерированной по равномерному, показательному или нормальному законам распределения, а также по выборке, введённой с клавиатуры. Кроме того, пользователю предоставляется возможность проведения исследований статистических оценок функции и плотности распределения от n – объёма выборки.

Интеграция разработанного программного комплекса в LMS Blackboard

Выполним описание процедуры внедрения программного комплекса в среду LMS Blackboard, используя руководство по работе в системе [6, с. 36–54].

1.  Переходим в интересующий нас курс. В данном случае это «Теория вероятности и математическая статистика». Режим редактирования должен быть включен: .

2.  Переходим во вкладку Content Collection в меню «Управление курсом» (рис. 3).

Рисунок 3. Меню «Управление курсом» в LMS Blackboard

3.  Выбираем выделенную нам область в базе данных LMS Blackboard (рис. 4).

Рисунок 4. Выбор курса в Content Collection

4.  Создаем папку. Чтобы наши данные лежали структурированно (рис. 5).

Рисунок 5. Создание папки для записи программ

После создания папки, выбираем «Отправить», затем в выпадающем меню «Загрузить пакет». Далее все файлы программного комплекса необходимо поместить в архив формата “ZIP”. После чего нажимаем кнопку “Обзор” и выбираем наш архив (рис. 6).

Рисунок 6. Добавление Zip-архива

После загрузки Zip-архива с программами в Content Collection настраивается точка входа на необходимой странице электронного курса.

Пример выполнения программы в электронном курсе представлен на рис. 7.

Рисунок 7. Статистические оценки плотности распределения

В настоящее время исследования по разработке интерактивных электронных образовательных ресурсов с помощью технологии JavaScript в КНИТУ-КАИ продолжаются.