Модульный принцип построения нечетких контроллеров

Application fuzzy logic to controller constructing

Oleg Rogozin

Cand. tech. Sci., Assoc., MSTU. Bauman N.E., Russia, Moscow

Аннотация. В данной статье предложен модульный принцип построения нечетких контроллеров, на основе которого может быть обеспечена разработка контроллера нечеткой логики, реализующего на аппаратном уровне управление некоторым техническим объектом. Рассмотрены структурный и топологический аспекты нечеткого контроллера и сформулированы общие правила построения контроллера с помощью стандартных блоков, обеспечивающих его использование в различных предметных областях.

Abstract This article gives an overview of realization variant of fuzzy inference mechanism providing the basis of developing fuzzy logic controller to manipulate some technical device on hardware level in automatic mode. It is given structural and topological aspects of fuzzy controller and also common rules for constructing a controller from unified modules accommodating controller use in different application domain.

Ключевые слова: нечеткая логика; лингвистическая переменная; технический объект; автоматическое управление; нечеткий контроллер; блок; модуль; приоритет правил вывода.

Keywords: fuzzy logic; linguistic variable; technical object; automatic control; fuzzy controller; block; module; fuzzy rules priority.

Для решения задачи  построения контроллера необходимы стандартные блоки, из которых можно было бы “собирать” необходимый контроллер. Логично установить соответствие между основными понятиями нечеткой логики (переменная и терм) и блоками контроллера. В таком случае различные способы соединения этих блоков между собой позволят отражать различные правила поведения системы. Таким образом, необходимо рассмотреть структурный и топологический аспекты нечеткого контроллера.

Первый этап нечеткого вывода состоит в том, что показания датчиков {} (четкие значения входных переменных) необходимо преобразовать к нечетким значениям входных переменных . Показание одного датчика определяет степень истинность равенства входной переменной, соответствующей этому датчику, каждому терму этой переменной. Степень истинности определяется на основе имеющегося определения нечеткого множества, соответствующего терму. Если имеется показание датчика х, то степень истинности равенства P = равна m, где (х, m).

Таким образом, один из типов блоков нечеткого контроллера должен обеспечивать задание нечеткого множества, который будет соответствовать термам параметров системы. Назовем этот блок “блок фазификации” и  будем обозначать его блок “x-m”. Заметим, что для всех термов переменных, задействованных на этапе фазификации – все входные переменные – в схеме контроллера должен будет присутствовать блок “x-m”.

Однако возможен более упрощенный подход. Задание нечеткого множества можно осуществить с помощью функции, график которой имеет треугольный вид (см. Рис.3).

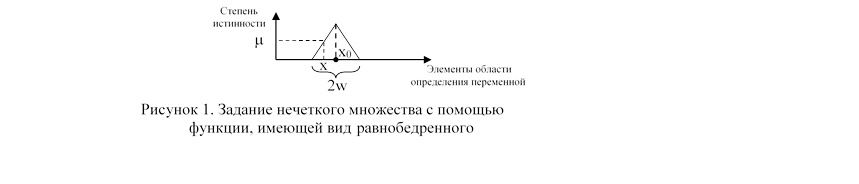
В этом случае функция соответствия четкого значения х и степени истинности m будет иметь вид:

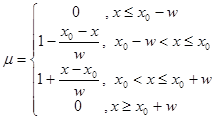
При упрощенной реализации определения нечеткого множества с помощью блока контроллера достаточно вместо таблицы хранить два числа: х₀ – центр основания равнобедренного треугольника, w –длина половины основания равнобедренного треугольника. Высота треугольника устанавливается за 1. При любом варианте реализации блока “x-m”, входом этого блока должно является числовое значение из области определения переменной, а на выходе число из отрезка [0,1], определяющее степень принадлежности значения к терму переменной, которой соответствует этот блок. В дальнейших рассуждениях будем полагать, что блок “x-m” реализован по упрощенной схеме. Как было замечено ранее, блок фазификации должен соответствовать терму входной переменной. Выделим модуль в схеме контроллера, соответствующий каждой входной переменной. Назовем его I-модуль.

В каждый модуль поместим столько блоков “x-m”, сколько имеет входная переменная, сопоставленная выбранному модулю. Блоки необходимо запрограммировать так, чтобы они реализовывали определение нечетких множеств, полученных при анализе задачи предметной области. Для реализации этапа композиции решений необходим K-модуль. Рассмотрим его задачу и структуру. Задача этапа композиции состоит в том, чтобы сгруппировать все правила с одинаковым консеквентом (совпадать должны переменная и терм правой части правила) и сформировать единое нечеткое значение переменной, относительно выбранного терма.

Каждый K-модуль соответствует промежуточной переменной. Входами являются пары сигналов (m,p), где m - сигнал с выхода I-модуля, или K-модуля, а p – сигнал, передающий значение весового коэффициента для находящегося в паре m-сигнала. P-сигнал формируется из значения приоритета правила, согласно которому осуществлена связь входа и выхода двух модулей. О правиле связи модулей будет рассказано ниже при определении топологических связей в нечетком контроллере. Выходами являются также пары сигналов (m,p), число которых равняется количеству термов переменной, соответствующей данному K-модулю. Выходной сигнал  m определяет степень истинности равенства переменной своему терму, к которому относится данный m сигнал, а следующий в паре сигнал p определяет весовое значение сигнала m при осуществлении композиции с другими m  сигналами.

На Рис.1 показана ситуация, когда для одного и того же терма Т₁ поступают сведения о том, что переменная M принимает это нечеткое значение (значение T₁) со степенью истинности m₁ и m₂ и имеющими свое весовое значение приоритета p₁ и p₂ соответственно. Для группировки поступающих сигналов к одному терму будем использовать формулу взвешенного среднего

                                                                                                        (1)

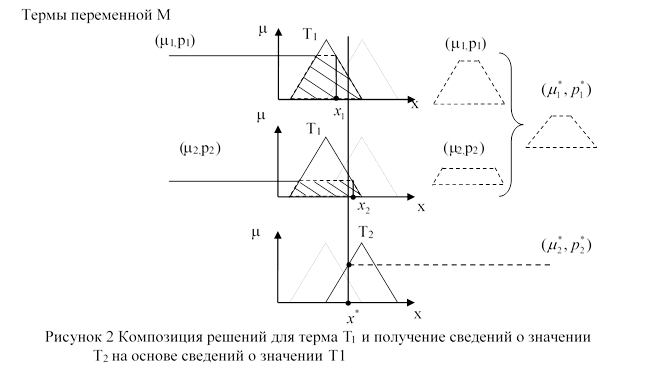
Чтобы определить значение приоритета p^* у объединенного решения воспользуемся принципом, продиктованным заключительным этапом нечеткого логического вывода – дефазификации. При получении четкого решения определяется центр масс фигуры, получаемой объединением фигур, соответствующих каждому терму, и образованных графиком характеристической функции терма и горизонтальной линией, проходящей на уровне степени истинности для этого терма. На Рис.1 показана фигура, соответствующая терму T₁ в виде пунктирной “трапеции”. Принцип объединения утверждает, что если рассматривать значение приоритета в качестве плотности фигуры, то масса объединяемых фигур должна равняться массе полученной фигуры, то есть

,                                                                                        (2)

где S(m)- площадь фигуры.

В нашем случае получаемые фигуры имеют вид трапеций. Площадь трапеций равна

Воспользуемся формулой Тейлора для получения линейной формулы площади (для нас важно не само значение площади трапеции, а важно то, как определять компромиссное четкое решение с использованием показаний приоритета всех составляющих решения, поэтому такое приближение вполне допустимо)

Для определения значения степени истинности объединенного решения m^* мы воспользовались формулой взвешенного среднего. Необходимо определить приоритет p^* значения степени истинности, используя полученное равенство (2)

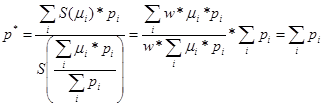                                                                        (3)

Итак, для композиции решений относительно одного терма переменной необходимо воспользоваться формулами (1) и (3) для получения степени истинности и приоритета значения степени истинности, определяющего нечеткое значение переменной. Теперь необходимо определить, как получать сведения о значении степени истинности для какого-либо терма на основе другого терма. На Рис.5 показана ситуация, как на основе сведений о значении терма T₁ можно получить сведения о значении терма T₂. Если обозначить плотность результирующей “трапеции” p, длину верхнего основания 2*x, центр нижнего основания х₀, то для термов, у которых центр основания соответствующих им графиков-трапеций расположен правее х₀ (этот случай показан на Рис.5. Терм Т2 расположен правее Т1) необходимо осуществить этап фазификации с входным четким значением для этого этапа, равным х^* =(х₀+х), а для термов, расположенных левее точки х₀ осуществить фазификацию с исходным четким значением х^* = (х₀-х). Можно показать, что значение х^* находится по формуле

,

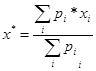где х_i  элемент из области определения переменной, принадлежащий нечеткому множеству, соответствующему данному терму, со степенью принадлежности m_i, причем  х_i расположен правее х₀ , если необходимо получить сведения о терме, расположенном правее рассматриваемого терма, и левее точки х₀ , если терм расположен левее. Для определения приоритета значения степени истинности  терма T₂ на основе сведений о степени истинности  и приоритета  терма T₂ можно использовать преобразование

Данная формула отражает тот факт, что получаемый приоритет  должен падать относительно , поскольку он соответствует терму, который не был получен при выводе явным образом. Коэффициент ½ является в определенном смысле эмпирическим и усиливает отличие приоритета терма , полученного явно, от приоритета терма , который получает свое значение косвенно, благодаря принадлежности  двух термов к одной лингвистической переменной.

Таким образом в К-модуле для одного терма необходимо 2 блока композиции (первый блок обеспечивает композицию для одного терма, второй обеспечивает поправку, учитывая влияние соседних термов), блок ассоциации, блок передачи приоритета и блок фазификации. На завершающем этапе необходимо получить четкое значение переменной на основе нечетких значений, полученных при композиции решений, и значениях приоритетов каждого нечеткого значения переменной.

Для завершающего этапа необходимо использовать O-модуль. По своей структуре он схож с K-модулем, однако к нему добавляется одни блок взвешенного среднего и блоки центра масс фигур, образованных графиками характеристических функций терма. В случае упрощенного подхода задания нечеткого множества положение центра масс определяется положением середины основания равнобедренного треугольника, задающего характеристическую функцию нечеткого множества для терма. Схема O-модуля показана на Рис. 3.

Заключение

Рассмотренный подход реализации механизма нечеткого вывода позволяет обеспечить разработку контроллера нечеткой логики и реализовать на аппаратном уровне управление некоторым техническим объектом, используя все преимущества методики нечеткого вывода. Использование нечеткого контроллера может расширить сферы применения систем автоматического регулирования и контроля на те области, в которых требуемое управляющие воздействие на систему не поддается формальному описанию с помощью традиционных подходов для этого класса задач.