РАСШИРЕННЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ МАКСВЕЛЛА
Конференция: LXVI Международная научно-практическая конференция «Научный форум: инновационная наука»
Секция: Физико-математические науки

LXVI Международная научно-практическая конференция «Научный форум: инновационная наука»
РАСШИРЕННЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ МАКСВЕЛЛА
EXTENDED MAXWELL'S EQUATIONS OF ELECTRODYNAMICS
Vladimir Filimonov
Ph.D. tech. Sciences, Art. scientific co-workers, JSC "Cryogenmash" in the city of Balashikha, Moscow region, Russia, Balashikha
Аннотация. Уравнения Максвелла расширены к виду, в котором учитываются скорости контрольной точки и источника полей. Формула закона электромагнитной индукции Фарадея расширена к виду, в котором наряду со скоростью замкнутого тока учитывается скорость источника магнитного потока. Формула Лоренца расширена к виду, в котором наряду со скоростью электрического заряда учитывается скорость источника поля.
Abstract. Maxwell's equations are extended to the form in which takes into account the speeds of the reference point and the source fields. Formula for Faraday's law of electromagnetic induction expanded to a form in which, along with the speed of the closed current the speed of the magnetic flux source is taken into account. Formula Lorentz is expanded to a form in which, along with speed electric charge, the speed of the field source is taken into account.
Ключевые слова: электродинамика; расширенные уравнения Максвелла; электромагнитная индукция Фарадея; формула Лоренца.
Keywords: electrodynamics; extended equations Maxwell; electromagnetic induction Faraday; formula Lorenz.
Теория электродинамики, как известно, основана на уравнениях Максвелла, а последние являются обобщением законов Кулона, Ампера, Фарадея, Гаусса, а также самого Максвелла, полученных на основе обобщения опытных фактов. Эти уравнения, были окончательно систематизированы и сформулированы Максвеллом еще в 1871 г. в труде "Трактат об электричестве и магнетизме", получив в дальнейшем название "Уравнения Максвелла". В своем классическом виде уравнения Максвелла определяют динамику электромагнитных явлений в неподвижной системе координат. Что касается движущихся электрических и магнитных полей, то для описания электромагнитных явлений в них, в той или иной форме используются формула Лоренца [11, с. 154]. Отдельные аналитические исследования по электродинамике движущихся полей представлены также в работах [7; 10; 13]. Однако, в литературе известно достаточно много электрических и магнитных явлений в движущихся полях, которые с точки зрения их физического объяснения являются дискуссионными [4; 9; 11; 12]. Ввиду этого представляется, что развитие последовательной теории электродинамики и в настоящее время является актуальной научной проблемой. В настоящей работе поставлена задача: доработать уравнения Максвелла с тем, чтобы они правильно описывали электромагнитные явления с учетом движущихся полей, зарядов и токов в свободном пространстве.
Для решения поставленной задачи произведем анализ уравнений Максвелла в рационализированной системе единиц Хевисайда – Лоренца, [3, с. 677], которые представим в виде:
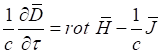 , (1)
, (1)
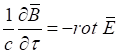 , (2)
, (2)
![]() , (3)
, (3)
![]() , (4)
, (4)
где ![]() − напряженность магнитного поля, [г1/2.см-1/2.сек--1];
− напряженность магнитного поля, [г1/2.см-1/2.сек--1]; ![]() − индукция магнитного поля, [г1/2.см-1/2.сек--1];
− индукция магнитного поля, [г1/2.см-1/2.сек--1]; ![]() − напряженность электрического поля, [г1/2.см-1/2.сек--1];
− напряженность электрического поля, [г1/2.см-1/2.сек--1]; ![]() − индукция электрического поля, [г1/2.см-1/2.сек--1];
− индукция электрического поля, [г1/2.см-1/2.сек--1]; ![]() − плотность тока, [г1/2.см-1/2.сек--2];
− плотность тока, [г1/2.см-1/2.сек--2]; ![]() − время, [сек];
− время, [сек]; ![]() − объемная плотность электрических зарядов, [г1/2.см-3/2.сек--1];
− объемная плотность электрических зарядов, [г1/2.см-3/2.сек--1]; ![]() − постоянный коэффициент, называемый электродинамической постоянной, равный скорости распространения электромагнитных волн в пустоте, [см-.сек-1]. Здесь и далее векторные величины обозначаются символами с надчерком. Система уравнений (1) – (4) дополняется также материальными уравнениями:
− постоянный коэффициент, называемый электродинамической постоянной, равный скорости распространения электромагнитных волн в пустоте, [см-.сек-1]. Здесь и далее векторные величины обозначаются символами с надчерком. Система уравнений (1) – (4) дополняется также материальными уравнениями:
![]() ,
, ![]() ,
, ![]() , (5)
, (5)
где ![]() − относительная магнитная проницаемость вещества;
− относительная магнитная проницаемость вещества; ![]() − относительная диэлектрическая проницаемость вещества;
− относительная диэлектрическая проницаемость вещества; ![]() − удельная проводимость среды, [сек--1].
− удельная проводимость среды, [сек--1].
Заметим, что подробный анализ истории создания уравнений Максвелла был представлен в 2006 году С.А. Сальлем в его статье "Истоки и заблуждения релятивизма. Взгляд через столетие" [12]. В своей статье Салль утверждает, что уравнения Максвелла были искажены в свое время создателями современной классической электродинамики − британскими физиками Д.Фицджеральдом и О. Хевисайдом. Дело в том, что Максвелл разрабатывал теорию электродинамики с использованием математического аппарата кватернионов, который был мало известен современникам в семнадцатом веке. В 1882 г. Хевисайд начал применять в электродинамике вместо математического аппарата кватернионов аппарат векторного анализа, а в 1883 г. ирландским физиком Дж. Фицджеральдом уравнения Максвелла были преобразованы из кватернионов к векторному виду. При этом уравнения Максвелла были искажены тем, что в них индивидуальные производные ![]() были заменены на частные
были заменены на частные ![]() как в системе (1) – (4). Эти уравнения в различных вариациях используются в классической электродинамике и до настоящего времени. В действительности изначально Максвелл записал свои уравнения в индивидуальных производных. Ввиду этого, в настоящей работе вернемся к оригинальным уравнениям Максвелла, вернув обратно в уравнениях (1) – (4) полные производные
как в системе (1) – (4). Эти уравнения в различных вариациях используются в классической электродинамике и до настоящего времени. В действительности изначально Максвелл записал свои уравнения в индивидуальных производных. Ввиду этого, в настоящей работе вернемся к оригинальным уравнениям Максвелла, вернув обратно в уравнениях (1) – (4) полные производные ![]() вместо частных
вместо частных ![]() , то есть запишем их в виде
, то есть запишем их в виде
 , (6)
, (6)
 , (7)
, (7)
![]() , (8)
, (8)
![]() . (9)
. (9)
Принципиальное отличие уравнений (1–4) от уравнений (6–9) заключается в том, что первые не сохраняют свой вид при преобразовании координат, а вторые – сохраняют. Независимость законов физики, записанных в виде формул, при их преобразованиях из одной системы координат в другую в условиях равномерного относительного движения этих систем, называется галилей-инвариантностью. Салль в своей статье доказывает галилей-инвариантность уравнений (6–9). Впрочем Галилей-инвариантность этих уравнений можно доказать и без сложных математических выкладок, если использовать известные законы векторного анализа. Для этого сначала обратимся к работе [1], в которой доказывается, что скалярные величины, векторы, а также дивергенция, градиент и ротор векторных полей являются инвариантными относительно преобразования координат, то есть при переходе из одной системы координат к другой они не изменяются. Ввиду этого в формулах (6–9) необходимо доказывать галилей-инвариантность только для полных производных ![]() и
и ![]() . Однако, инвариантность полных производных также известна и доказывается в монографии [2, с. 397]. Таким образом, уравнения (6–9) являются галилей-инвариантными.
. Однако, инвариантность полных производных также известна и доказывается в монографии [2, с. 397]. Таким образом, уравнения (6–9) являются галилей-инвариантными.
Полные производные по времени используются обычно в гидродинамике для описания каких-либо свойств в частице материальной среды, движущейся вместе с потоком этой среды со скоростью ![]() . При этом произвольная векторная функция, например
. При этом произвольная векторная функция, например ![]() , является сложной векторной функцией, зависящей от времени и координат, но координаты в движущейся системе также подчиняются времени [10, с. 359]. Ввиду этого, полная производная от сложной векторной функции преобразуется к частным производным по известной формуле [8, с. 129]
, является сложной векторной функцией, зависящей от времени и координат, но координаты в движущейся системе также подчиняются времени [10, с. 359]. Ввиду этого, полная производная от сложной векторной функции преобразуется к частным производным по известной формуле [8, с. 129]
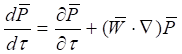 , (10)
, (10)
где ![]() − скорость потока материальной среды,
− скорость потока материальной среды, ![]() − оператор Гамильтона.
− оператор Гамильтона.
В настоящей статье для анализа силовых электрических и магнитных полей в условиях равномерного движения, как источника поля, так и контрольной точки, будет использован аналогичный математический прием. Здесь под термином "контрольная точка" имеется ввиду точка, в которой измеряются параметры электрического и магнитного полей. В монографии [14, с. 127], было показано, что полная производная произвольного силового векторного поля, обозначенного, например, как ![]() , по времени преобразуется к частным производным по формуле, аналогичной соотношению (11.10), но с учетом разности равномерных скоростей источника поля и контрольной точки, то есть
, по времени преобразуется к частным производным по формуле, аналогичной соотношению (11.10), но с учетом разности равномерных скоростей источника поля и контрольной точки, то есть
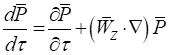 , (11)
, (11)
![]() , (12)
, (12)
где![]() − силовое векторное поле;
− силовое векторное поле; ![]() − скорость контрольной точки;
− скорость контрольной точки; ![]() − скорость источника поля;
− скорость источника поля; ![]() − относительная скорость, определяемая соотношением (12).
− относительная скорость, определяемая соотношением (12).
Произведем анализ системы уравнений (6−9) на предмет преобразования этих уравнений из полных производных к частным. С этой целью в рассматриваемых уравнениях представим преобразования полных производных по времени ![]() и
и ![]() к частным производным по аналогии с уравнением (11) как:
к частным производным по аналогии с уравнением (11) как:
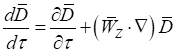 , (13)
, (13)
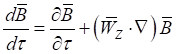 . (14)
. (14)
Соотношения (13) и (14) определяют преобразование индивидуальных производных ![]() и
и ![]() к частным производным в уравнениях (6) и (7) соответственно. Подставив соотношение (13) в уравнение (6), а соотношение (14) − в уравнение (7), запишем:
к частным производным в уравнениях (6) и (7) соответственно. Подставив соотношение (13) в уравнение (6), а соотношение (14) − в уравнение (7), запишем:
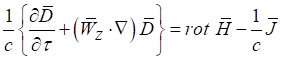 , (15)
, (15)
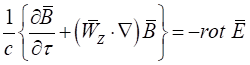 . (16)
. (16)
Преобразуем в соотношениях (15) второе слагаемое к виду, более удобному для дальнейшего анализа. С этой целью используем известное векторное тождество (см. приложение А.11). Заменив в этом тождестве векторы ![]() и
и ![]() , запишем:
, запишем:
![]() . (17)
. (17)
Поскольку ![]() , то второе и третье слагаемые в правой части этого соотношения обратятся в ноль. Ввиду этого, соотношение (17) упростится к виду:
, то второе и третье слагаемые в правой части этого соотношения обратятся в ноль. Ввиду этого, соотношение (17) упростится к виду:
![]() . (18)
. (18)
Преобразуем также в уравнении (16) оператор ![]() к виду, удобному для дальнейшего анализа. С этой целью запишем тождество (А.11), где обозначим
к виду, удобному для дальнейшего анализа. С этой целью запишем тождество (А.11), где обозначим ![]() и
и ![]() , то есть
, то есть
![]() . (19)
. (19)
Поскольку скорость контрольной точки ![]() принята постоянной, то вторые и третьи слагаемые в правой части этого соотношения равны нулю. Приняв во внимание выражение (9), получим, что и четвертое слагаемое в соотношении (19) равно нулю. Ввиду этого соотношение (19) упростится к виду:
принята постоянной, то вторые и третьи слагаемые в правой части этого соотношения равны нулю. Приняв во внимание выражение (9), получим, что и четвертое слагаемое в соотношении (19) равно нулю. Ввиду этого соотношение (19) упростится к виду:
![]() . (20)
. (20)
Вернемся вновь к уравнениям (15) и (16). Исключив из уравнений (15) и (16) выражения ![]() и
и ![]() посредством соотношений (18) и (20), представим полученные уравнения) в виде:
посредством соотношений (18) и (20), представим полученные уравнения) в виде:
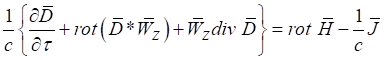 , (21)
, (21)
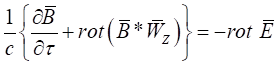 . (22)
. (22)
Таким образом, уравнения (6) и (7) с индивидуальными производными по времени преобразованы соответственно к уравнениям в частных производных (21) и (22).
Вернемся вновь к уравнениям (1−4) и рассмотрим уравнение (3). В классической электродинамике известно, что это уравнение получается путем взятия дивергенции от уравнения (1) и решения полученного уравнения с формулой закона сохранения электрического заряда. Представим закон сохранения электрического заряда в виде [6, с. 128], то есть
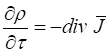 . (23)
. (23)
Для определения уравнения (3) применительно к условию движения источника поля и контрольной точки, возьмем дивергенцию от уравнения (21). Приняв во внимание, что дивергенция от ротора равна нулю (А02.4), получим:
 . (24)
. (24)
Сократив это уравнение на константу "с" и исключив из этого уравнения оператор ![]() подстановкой формулы (23), получим:
подстановкой формулы (23), получим:
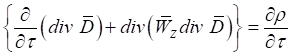 . (25)
. (25)
Вынеся производную по времени за общие скобки, преобразуем уравнение (25) к виду:
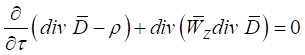 . (26)
. (26)
Преобразуем второе слагаемое в этом уравнении к виду, более удобному для дальнейшего анализа. С этой целью обратимся к тождеству (А02.7), где заменим переменные в виде ![]() и
и ![]() , то есть:
, то есть:
![]() . (27)
. (27)
Поскольку вектор ![]() − постоянная величина, то
− постоянная величина, то ![]() и соотношение (27) упрощается к виду:
и соотношение (27) упрощается к виду:
![]() . (28)
. (28)
Подставив во второе слагаемое уравнения (26) соотношение (28), получим:
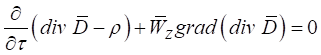 . (29)
. (29)
Соберем полученные выше уравнения (21), (22), (29), (4) и (12) в единую систему, причем, вместо вектора ![]() подставим соотношение (12). В результате получим:
подставим соотношение (12). В результате получим:
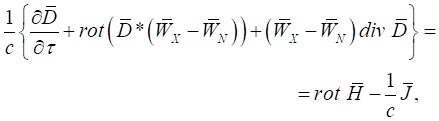 (30)
(30)
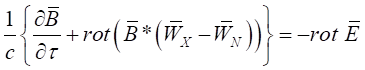 , (31)
, (31)
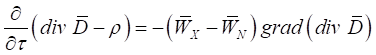 , (32)
, (32)
![]() . (33)
. (33)
Уравнения (30–33) определяют динамическую взаимосвязь электрического и магнитного полей, а также зарядов ![]() и токов
и токов ![]() в контрольной точке, движущейся с равномерной скоростью
в контрольной точке, движущейся с равномерной скоростью ![]() в относительно неподвижной системе координат, причем, источник этих полей движется в другой области этой же системы с равномерной скоростью
в относительно неподвижной системе координат, причем, источник этих полей движется в другой области этой же системы с равномерной скоростью ![]() .
.
Нетрудно видеть, что в условиях относительной неподвижности источника поля и контрольной точки, то есть при ![]() , уравнения (30−33) сводятся к уравнениям Максвелла (1−4). Согласно этому уравнению:
, уравнения (30−33) сводятся к уравнениям Максвелла (1−4). Согласно этому уравнению:
(30−33) предлагается называть расширенными уравнениями Максвелла.
По поводу полученных выше уравнений дадим следующие разъяснения. Как известно, все параметры в уравнении должны относиться к одной точке пространства. Может показаться странным присутствие в уравнениях (30−33) параметра ![]() , определяющего скорость источника поля, находящегося не в контрольной точке, а в другой области пространства. Из опыта известно, что электрические и магнитные поля движутся вместе со своими источниками с той же скоростью. Поэтому, задавая скорость источника, находящегося неизвестно где, мы задаем скорость его полей в контрольной точке. Таким образом, скорость
, определяющего скорость источника поля, находящегося не в контрольной точке, а в другой области пространства. Из опыта известно, что электрические и магнитные поля движутся вместе со своими источниками с той же скоростью. Поэтому, задавая скорость источника, находящегося неизвестно где, мы задаем скорость его полей в контрольной точке. Таким образом, скорость ![]() в уравнениях (30−33) − это фактически скорость движения электрических и магнитных полей в контрольной точке.
в уравнениях (30−33) − это фактически скорость движения электрических и магнитных полей в контрольной точке.
Рассмотрим некоторые следствия, вытекающие из уравнений (30−33). Проанализируем вывод закона электромагнитной индукции Фарадея с учетом движущихся координат. С этой целью обратимся к блоку уравнений (30−33) и преобразуем второе уравнение (31) к интегральному виду. С этой целью, подставив в рассматриваемое уравнение для компактности формулу (12), проинтегрируем его по некоторой не замкнутой поверхности ![]() как:
как:
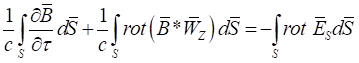 , (35)
, (35)
где ![]() − произвольная, незамкнутая поверхность в пространстве.
− произвольная, незамкнутая поверхность в пространстве.
Преобразуем первый интеграл в левой части этого уравнения. Поменяв порядок интегрирования и дифференцирования, запишем этот интеграл в виде:
 . (36)
. (36)
Преобразуем также второй интеграл левой части уравнения (35) из поверхностного в линейный по известной формуле Стокса как:
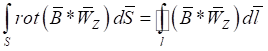 . (37)
. (37)
Преобразуем интеграл в правой части уравнения (35) из поверхностного в линейный по формуле Стокса, то есть:
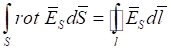 , (38)
, (38)
где ![]() − линия, охватывающая поверхность
− линия, охватывающая поверхность ![]() ;
;
![]() − вектор бесконечно малого отрезка лини
− вектор бесконечно малого отрезка лини ![]() .
.
Подставив интегралы (36), (37) и (38) в уравнение (35), запишем:
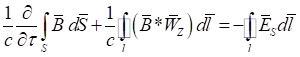 . (39)
. (39)
Уравнение (39) представляет собой интегральную форму дифференциального уравнения (31). Интеграл в левой части уравнения (39) в электродинамике определяется как магнитный поток ![]() [5, с. 219], то есть:
[5, с. 219], то есть:
![]() , (40)
, (40)
где ![]() − магнитный поток.
− магнитный поток.
Интеграл в правой части уравнения (39) представляет собой электродвижущую силу ![]() в замкнутом контуре
в замкнутом контуре ![]() , то есть:
, то есть:
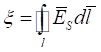 , (41)
, (41)
где ![]() − электродвижущая сила (ЭДС) в проводящем контуре
− электродвижущая сила (ЭДС) в проводящем контуре ![]() , определяемая как работа, затрачиваемая на перемещение единицы электрического заряда по замкнутому контуру
, определяемая как работа, затрачиваемая на перемещение единицы электрического заряда по замкнутому контуру ![]() . Подставив определения (40) и (41) в уравнение (39) и поменяв во втором слагаемом порядок перемножения в векторном произведении с соответствующим изменением знаков, получим:
. Подставив определения (40) и (41) в уравнение (39) и поменяв во втором слагаемом порядок перемножения в векторном произведении с соответствующим изменением знаков, получим:
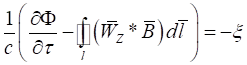 . (42)
. (42)
Подставив сюда формулу (12), запишем:
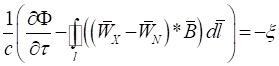 , (43)
, (43)
где ![]() − скорость контура;
− скорость контура;
![]() − скорость источника магнитного потока
− скорость источника магнитного потока ![]() .
.
Уравнение (43) определяет зависимость электродвижущей силы ![]() (ЭДС), возникающей в замкнутом электропроводящем контуре, при изменении магнитного потока
(ЭДС), возникающей в замкнутом электропроводящем контуре, при изменении магнитного потока ![]() , внутри этого контура, а также при движении рассматриваемого контура в магнитном потоке с индукции
, внутри этого контура, а также при движении рассматриваемого контура в магнитном потоке с индукции ![]() со скоростью
со скоростью ![]() и при движении источника магнитного потока со скоростью
и при движении источника магнитного потока со скоростью ![]() . Принципиальное отличие уравнения (43) от известного уравнения электромагнитной индукции Фарадея [6, с. 248] заключается в том, что здесь при определении ЭДС в замкнутом контуре наряду с изменением магнитного потока
. Принципиальное отличие уравнения (43) от известного уравнения электромагнитной индукции Фарадея [6, с. 248] заключается в том, что здесь при определении ЭДС в замкнутом контуре наряду с изменением магнитного потока ![]() и движением замкнутого контура со скоростью
и движением замкнутого контура со скоростью ![]() , учитывается также скорость движения
, учитывается также скорость движения ![]() источника магнитного потока. Ввиду этого, уравнение (43) предлагается называть расширенной формулой электромагнитной индукции Фарадея.
источника магнитного потока. Ввиду этого, уравнение (43) предлагается называть расширенной формулой электромагнитной индукции Фарадея.
Вернемся теперь вновь к уравнениям (30–33). Решение этих уравнений в общем виде для ряда задач может оказаться проблематичным, поэтому для получения конкретных расчетных формул прибегают к упрощающим допущениям. К таким упрощающим допущениям можно рассматривать переход к стационарным процессам, при которых поля, заряды и токи в любой точке пространства остаются постоянными. Простейшим примером стационарного процесса является постоянный электрический ток, создающий в пространстве постоянное магнитное поле. Многие законы электродинамики, такие как формула силы Лоренца, закон Био-Савара, теорема о циркуляции магнитного поля и ряд других также предполагают стационарность процесса. Поскольку в настоящей работе получены расширенные уравнения Максвелла (30–34), то при выводе на их основе ряда закономерностей также получается расширение. Ввиду этого, рассмотрим некоторые стационарные процессы, определяемые уравнениями (30–33). Для этого предположим, в рассматриваемых уравнениях динамические члены равны нулю, то есть:
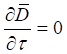 и
и 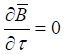 , (44)
, (44)
а также:
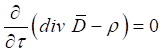 , (45)
, (45)
откуда следует ![]() . В результате, при условии
. В результате, при условии ![]() преобразуем уравнения (30−33) к виду:
преобразуем уравнения (30−33) к виду:
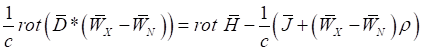 , (46)
, (46)
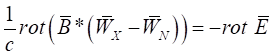 , (47)
, (47)
![]() , (48)
, (48)
![]() . (49)
. (49)
Уравнения (46−49) определяют стационарную взаимосвязь напряженности электрического и магнитного полей при заданных функциях плотности тока ![]() и плотности электрических зарядов
и плотности электрических зарядов ![]() в контрольной точке, движущейся равномерно со скоростью
в контрольной точке, движущейся равномерно со скоростью ![]() , при том, что источник этих полей движется с равномерной скоростью
, при том, что источник этих полей движется с равномерной скоростью ![]() .
.
Проанализируем вывод формулы Лоренца с точки зрения расширенных уравнений Максвелла. С этой целью обратимся к уравнению (47), в котором подставим соотношение (12) для сокращения выкладок и вынесем оператор ротора за общие скобки. В результате получим:
 . (51)
. (51)
Формула (51) удовлетворяется при равенстве выражения, заключенного в скобки, градиенту от произвольной скалярной функции, то есть:
 , (52)
, (52)
где ![]() − произвольная скалярная функция.
− произвольная скалярная функция.
Для проверки правильности соотношения (52) возьмем от него операцию ротора. Приняв во внимание, что ротор от градиента равен нулю (А.3), получим вновь соотношение (51), что подтверждает правильность проделанных операций. Правая часть формулы (52) представляет собой потенциальное векторное поле, которое обозначим как:
![]() , (53)
, (53)
где ![]() − векторное поле, определяемое условием:
− векторное поле, определяемое условием:
![]() . (54)
. (54)
Для проверки справедливости соотношения (54) возьмем операцию ротора от выражения (53). Приняв во внимание, что ротор от градиента равен нулю (А.3), получим соотношение (54). Для определения векторного поля ![]() проанализируем электрическое поле
проанализируем электрическое поле ![]() , в уравнениях Максвелла. Поскольку на это поле не наложено никаких ограничений, то его можно разложить по теореме разложения Гельмгольца на потенциальную и соленоидальную составляющие как:
, в уравнениях Максвелла. Поскольку на это поле не наложено никаких ограничений, то его можно разложить по теореме разложения Гельмгольца на потенциальную и соленоидальную составляющие как:
![]() , (55)
, (55)
где:
![]() ; (56)
; (56)
![]() . (57)
. (57)
Здесь соотношение (56) определяет потенциальность векторного поля ![]() , а соотношение (57) – соленоидальность векторного поля
, а соотношение (57) – соленоидальность векторного поля ![]() . Таким образом, выражение (55) определяет, что напряженность электрического поля
. Таким образом, выражение (55) определяет, что напряженность электрического поля ![]() представляет собой сумму из потенциального
представляет собой сумму из потенциального ![]() и соленоидального
и соленоидального ![]() полей.
полей.
Обратимся вновь к уравнению (52) и определим напряженность электрического поля ![]() по определению как силу, действующую на единицу электрического заряда. Ввиду этого вектор
по определению как силу, действующую на единицу электрического заряда. Ввиду этого вектор ![]() определим как силу, деленную на величину заряда, то есть:
определим как силу, деленную на величину заряда, то есть:
![]() . (58)
. (58)
Подставив соотношения (53) и (55) в формулу:
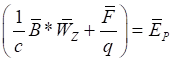 . (59)
. (59)
Или:
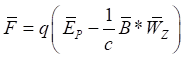 . (60)
. (60)
Поменяв в векторном произведении порядок перемножения с соответствующим изменением знака, а также подставив в полученное выражение соотношение (12), получим:
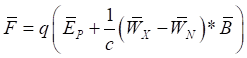 , (61)
, (61)
где ![]() − равномерная скорость контрольной точки, совпадающей со скоростью движения электрического заряда;
− равномерная скорость контрольной точки, совпадающей со скоростью движения электрического заряда;
![]() − равномерная скорость движения источника магнитного поля.
− равномерная скорость движения источника магнитного поля.
Формула (61) определяет в относительно неподвижной системе координат силу ![]() , действующую на электрический заряд
, действующую на электрический заряд ![]() , движущегося со скоростью
, движущегося со скоростью ![]() в электрическом поле с напряженностью
в электрическом поле с напряженностью ![]() и в магнитном поле с магнитной индукцией
и в магнитном поле с магнитной индукцией ![]() , притом, что сам источник магнитного поля движется со скоростью
, притом, что сам источник магнитного поля движется со скоростью ![]() в другой области той же системы координат.
в другой области той же системы координат.
Проанализируем несколько частных случаев, вытекающих из уравнения (61). Если скорость источника магнитного поля (магнита) и скорость заряда одинаковы, то есть ![]() , то формула (61) упрощается к виду:
, то формула (61) упрощается к виду:
![]() . (62)
. (62)
Как видим, в этом случае на электрический заряд действует лишь электрическая сила. На практике это означает, что если в поле постоянного подковообразного магнита находится электрический заряд, то при движении их с одинаковой скоростью, магнитная сила будет отсутствовать.
Рассмотрим другой частный случай, вытекающий из уравнения (61). Примем, что источник поля неподвижен, то есть ![]() . В этом случае формула (61) упрощается к известной формуле Лоренца [6, с.154], то есть:
. В этом случае формула (61) упрощается к известной формуле Лоренца [6, с.154], то есть:
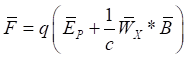 . (63)
. (63)
Наконец, можем рассмотреть третий случай, когда заряд, расположенный в контрольной точке, неподвижен, то есть ![]() , а источник магнитного поля движется со скоростью
, а источник магнитного поля движется со скоростью ![]() . Для этого случая формула (61) примет вид
. Для этого случая формула (61) примет вид
 . (64)
. (64)
Формула (64) определяет силу ![]() , действующую на неподвижный электрический заряд
, действующую на неподвижный электрический заряд ![]() , находящийся в электрическом поле с напряженностью
, находящийся в электрическом поле с напряженностью ![]() и в магнитном поле источника с индукцией
и в магнитном поле источника с индукцией ![]() , движущегося со скоростью
, движущегося со скоростью ![]() в этой системе. Эта формула по своей структуре сходна с формулой Лоренца (63), но отличается знаком в правой части и индексом скорости
в этой системе. Эта формула по своей структуре сходна с формулой Лоренца (63), но отличается знаком в правой части и индексом скорости ![]() . На практике это означает, что если в электрическом поле (если оно есть) и в поле постоянного подковообразного магнита находится неподвижный электрический заряд, то при движении магнита со скоростью
. На практике это означает, что если в электрическом поле (если оно есть) и в поле постоянного подковообразного магнита находится неподвижный электрический заряд, то при движении магнита со скоростью ![]() относительно неподвижного заряда, − на последний наряду с электрической силой, будет действовать магнитная сила, определяемая формулой (64).
относительно неподвижного заряда, − на последний наряду с электрической силой, будет действовать магнитная сила, определяемая формулой (64).
Таким образом, принципиальное отличие формулы (61) от формулы Лоренца (63) заключается в том, что здесь при определении силы ![]() , действующей на электрический заряд
, действующей на электрический заряд ![]() , учитывается не только электрическое поле
, учитывается не только электрическое поле ![]() , магнитное поле
, магнитное поле ![]() и скорость электрического заряда
и скорость электрического заряда ![]() , но и скорость источника
, но и скорость источника ![]() магнитного поля. Ввиду этого предлагается называть уравнение (61) расширенной формулой Лоренца.
магнитного поля. Ввиду этого предлагается называть уравнение (61) расширенной формулой Лоренца.
Выводы
- Произведен анализ уравнений Максвелла (1–4), в результате чего выведены расширенные уравнения Максвелла (30–33) с учетом движущихся контрольной точки и источника поля.
- Выведена расширенная формула закона Фарадея (43), отличающаяся тем, что в ней при определении ЭДС, возникающем в замкнутом электропроводящем контуре, наряду с учетом динамического изменения магнитного потока и с учетом скорости движения электропроводящего контура, также учитывается скорость движения источника магнитного потока
- Выведена расширенная формула Лоренца (61), отличающаяся тем, что в ней при определении силы, действующей на электрический заряд, движущейся в электрическом и магнитном полях задана не только скорость заряда, но и скорость источника магнитного поля.
Приложение А
Вторые производные
 , (А.1)
, (А.1)
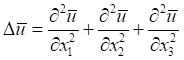 , (А.2)
, (А.2)
![]() , (А.3)
, (А.3)
![]() , (А.4)
, (А.4)
![]() . (А.5)
. (А.5)
Производные от произведений
![]() , (А.6)
, (А.6)
![]() , (А.7)
, (А.7)
![]() , (А.8)
, (А.8)
![]() , (А.9)
, (А.9)
![]() , (А.10)
, (А.10)
![]() . (А.11)
. (А.11)
Литература к приложению А [3].


