Алгоритм перебора всех возможных систем линейно независимых векторов, элементы которых принадлежат множеству {0,1}
Конференция: I Международная заочная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Математическая логика, алгебра и теория чисел

I Международная заочная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Алгоритм перебора всех возможных систем линейно независимых векторов, элементы которых принадлежат множеству {0,1}
Algorithm of searching all possible linearly independent systems of vectors which elements belong to the set
Dodonova Natalia Leonidovna
Candidate of Physics and Mathematics, assistant professor in Samara University, Russia, Samara
Khantova Anna Dmitrievna
Student , faculty of informatics, mathematics and electronics of Samara University, Russia, Samara
Аннотация. В работе представлен алгоритм перебора всех возможных линейно независимых систем векторов, элементы которых принадлежат множеству {0,1}. Доказано, что все системы различны между собой и выбраны все возможные варианты.
Abstract. There is an algorithm of searching all possible linearly independent systems of vectors which elements belong to the set {0, 1} in the work. It is proved that all systems are different and all possible systems are selected.
Ключевые слова: линейно независимая система векторов.
Keywords: linearly independent systems of vectors.
Рассмотрим матрицу М размера [k,n] где каждый элемент принадлежит множеству {0,1}.
Правило произведения: если элемент a можно выбрать m способами и независимо от него элемент b выбрать n способами, то все различные комбинации элементов «a и b» можно выбрать m*n способами. При этом пара (a, b) отличается от пары (b, a).Следовательно, первый элемент совокупности из k элементов можно выбрать n1 способами, второй – n2 способами и так далее, то количество вариантов, которыми можно выбрать вектор (b1,b2, … bk) равно n1*n2*…*nk.Таким образом, каждую строку матрицы М можно выбрать 2*2*…*2=2n способами.
Каждый способ выбора строки - вектор - обозначим wi. Тогда множество всех векторов-строк матрицы М - E1={![]() }. Тогда матрица М – это k элементов из множества E1. Значит, всего (2n)k = 2n*k всех возможных матриц, элементы которых принадлежат множеству {0,1}.Заметим, что если строить матрицу по столбцам, мы получим тот же результат – каждый столбец матрицы М можно выбрать 2k способами. Множество всех векторов-столбцов матрицы М - E1={
}. Тогда матрица М – это k элементов из множества E1. Значит, всего (2n)k = 2n*k всех возможных матриц, элементы которых принадлежат множеству {0,1}.Заметим, что если строить матрицу по столбцам, мы получим тот же результат – каждый столбец матрицы М можно выбрать 2k способами. Множество всех векторов-столбцов матрицы М - E1={![]() }. Тогда количество всех возможных матриц, элементы которых принадлежат множеству {0,1}, равно (2k)n= 2k*n.
}. Тогда количество всех возможных матриц, элементы которых принадлежат множеству {0,1}, равно (2k)n= 2k*n.
Матрица – система векторов. Система векторов e1,e2,…,el линейно независима (ЛНЗ) если линейная комбинация c1*e1+c2*e2+…+ck*ek представляет собой нулевой вектор только и только тогда, когда все числа ci равны нулю. Поскольку каждый элемент вектора может быть равен только 0 или 1,то и любой коэффициент ci принадлежит множеству {0,1}.
Согласно одному из свойств ЛЗ и ЛНЗ системы векторов, если в систему строк (столбцов) входит нулевая строка (столбец), то система ЛЗ. Значит, мы должны исключить нулевой вектор из множества векторов, из которого мы выбираем строки: E2=E1\w0={![]() }.Количество таких матриц
}.Количество таких матриц
(2n-1)k.
Система также является ЛЗ, если в неё входят одинаковые строки. Поэтому выбирать строки мы будем без повторений. Количество таких матриц можно посчитать по формуле (1).
![]() (1)
(1)
Алгоритм перебора всех возможных систем ЛНЗ векторов.
Имеется 2n-1 векторов. (![]() ) – список векторов. Составлять ЛНЗ системы будем по следующему алгоритму.
) – список векторов. Составлять ЛНЗ системы будем по следующему алгоритму.
Имеется k мест. S – номер места.
k k-1 … 3 2 1 - порядок нумерации мест.
На каждое место выбирается вектор из списка. Вектора не могут повторяться. Порядок векторов не важен. Поэтому в алгоритме при решении о включении вектора в систему мы можем рассматривать только вектора, находящиеся справа от текущего, т.к система векторов (![]() ) и, например, система векторов (
) и, например, система векторов (![]() ) будут считаться одной системой.
) будут считаться одной системой.
Считаем, что место на которое указывает текущее S и все места после него не заняты. Если на места были выбраны вектора, а после этого S переместился так, что эти места оказались после S , то они считаются освобожденными.
W[ S ] - вектор w на месте S
I (W[ S ]) – номер i вектора w на месте S
На начало алгоритма S=k, i=1, где i номер вектора.
1. На место k выбираем первый вектор из списка ![]() . Тогда S=k-1, i=2.
. Тогда S=k-1, i=2.
W1 s … __ __
k k-1 2 1
2. Если не превысили число векторов wi, т.е i<2n
2.1. Если вектор wi является линейной комбинацией предыдущих векторов Wi = Ci-1*Wi-1 + Ci-2*Wi-2 +...+ C1* W1 , где каждое ![]() , то не включаем этот вектор в систему, i= i+1 и переходим на шаг 2
, то не включаем этот вектор в систему, i= i+1 и переходим на шаг 2
2.2. Включаем в систему вектор Wi из списка, переходим на следующее место S = S-1
W1 Wi’ s … __ __
k k-1 k-2 2 1
2.3. Если S=0 , т.е мы выбрали вектора на все k мест,
W1 Wi ‘ … Wi s
k k-1 1 0
фиксируем полученную систему, S = S+1
W1 Wi ‘ … s _
k k-1 1 0
2.4. i= i+1, переходим на шаг 2
3. Если превысили число векторов wi, т.е i>2n
3.1. Если место текущего включаемого вектора S=k-1, и количество оставшихся векторов меньше, чем мест в системе 2n - I (W[ S ]) < k-1, то алгоритм завершен
3.2. Иначе I= I (W[ S+1 ])+1, S=S+1, и переходим на шаг 2
Данный алгоритм можно представить в виде блок-схемы (рисунок 1).

Рисунок 1 - Алгоритм перебора всех возможных ЛНЗ систем векторов
Из каждой полученной системы векторов - матрицы мы можем получить k! ЛНЗ матриц. Таким образом, перебор всех возможных ЛНЗ матриц можно представить в виде дерева высоты k+1 (рисунок 2). Каждая вершина дерева означает выбранный вектор на m-ое место, где m – ярус дерева. Вершина A0 на нулевом ярусе не соответствует никакому вектору и месту. Поскольку в алгоритме мы рассматривали только вектора, находящиеся справа от последнего включенного вектора, все потомки одного предка упорядочены по своему положению в списке слева направо от первого вектора в оставшемся списке до последнего возможного. Также каждая вершина-вектор потомок находится в списке правее вершины-вектора предка.
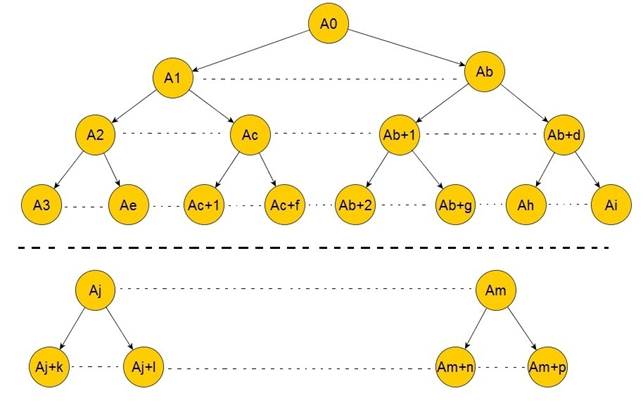
Рисунок 2 - Дерево выбора вектора
Каждая простая цепь от корня дерева до концевого узла является набором ЛНЗ векторов. Все наборы различны между собой, и перебрав все полученные с помощью дерева наборы ЛНЗ векторов, мы переберем все возможные варианты.
Доказательство:
1) Каждая простая цепь от корня дерева до концевого узла является набором векторов. Поскольку, согласно алгоритму, вектора в наборах не повторяются, а также на каждое i-ое место не включаются вектора, являющиеся линейной комбинацией предыдущих i-1 векторов в наборе, то каждая простая цепь от корня дерева до концевого узла является набором ЛНЗ векторов.
2) Поскольку все потомки одного предка упорядочены по своему положению в списке слева направо от первого вектора в оставшемся списке до последнего возможного, а каждая простая цепь от корня дерева до концевого узла является набором векторов, то все получившиеся наборы векторов будут различны.
3) Согласно алгоритму, мы включаем в систему подходящие векторы до тех пор, пока это возможно: пока есть места и не включенные еще вектора. Если одно из условий не соблюдается, мы «отходим» на позицию назад и ищем на эту позицию новый, еще не включавшийся вектор. При включении нового вектора, набор векторов удовлетворяющих условию Wi =Ci-1*Wi-1 + Ci-2*Wi-2 +...+ C1* W1 может измениться, поэтому мы заново просматриваем все вектора, начиная от i+1 к вектору, добавленному на предыдущую позицию. А т.к мы сохраняем все включенные вектора, за исключением последнего, то получается, что мы перебираем все варианты с «конца» системы


