СРАВНЕНИЕ РАЗЛИЧНЫХ ОПИСАНИЙ И РЕАЛИЗАЦИЙ АЛГОРИТМА ЛИСА ДЛЯ ПЕРКОЛЯЦИОННЫХ ЗАДАЧ

COMPARISION OF DIFFERENT DESCRIPTIONS AND IMPLEMENTATIONS OF THE LEATH ALGORITHM FOR PERCOLATION PROBLEMS

Ivan Gordeev

Candidate of Physical and Mathematical Sciences, Associate professor in Astrakhan State University, Russia, Astrakhan

Arina Pismenskaya

Student in Astrakhan State University, Russia, Astrakhan

Аннотация. При моделировании перколяционных задач являются актуальными различные свойства случайных кластеров. В случаях, когда требуется моделировать свойства отдельных кластеров, более удобным оказывается алгоритм, предложенный Полом Лисом [1]. Предложенный 45 лет назад алгоритм Лиса продолжает оставаться актуальным и активно использоваться исследователями в области перколяции в самых свежих работах.

Abstract. When modeling percolation problems, various properties of random clusters are relevant. In cases where it is required to model the properties of separate clusters, the algorithm proposed by Paul Leath [1] is more convenient. The Leath algorithm proposed 45 years ago continues to be relevant and actively used by researchers in the field of percolation in the most recent works.

Ключевые слова: перколяция; перколяционный кластер; алгоритм Лиса.

Keywords: percolation; percolation cluster; the Leath algorithm.

Введение. Теория перколяции активно применяется для моделирования различных явлений в неупорядоченных средах. Одним из методов моделирования перколяционных задач является алгоритм, первоначально описанный в статье Пола Лиса из Ратгерского университета (Нью-Браунсуик, Нью-Джерси, США) [8]. В целом ряде последующих публикаций алгоритм называют алгоритмом Лиса [10, c. 53, 156; 11, c. 287; 18, c. 64; 9; 2; 6]. Похожий алгоритм был описан в статье Зеэва Александровица из института Вейцмана (Реховот, Израиль) [1], поэтому в ряде публикаций алгоритм упоминается как алгоритм Лиса-Александаровица [14; 7; 12], но нередко алгоритм упоминается по фамилиям трех авторов как алгоритм Хаммерсли-Лиса-Александровица [17, c. 373; 15, c. 403; 16, c. 206, 214], поскольку идеи подобного алгоритма были сформулированы еще раньше в книге написанной Джоном Хаммерсли из Оксфордского университета (Оксфорд, Англия) совместно с его бывшим студентом Дэвидом Хэндскомбом [5], первое издание книги Хаммерсли и Хэндскомба вышло еще в 1964 году.

Хотя Лис опубликовал свою статью на 4 года раньше Александровица, в книге Харви Гулда и Яна Тобочника [17, с. 143] утверждается, что Александровиц описал алгоритм независимо. После книги Гудла и Тобочника утверждение о независимости разработки алгоритма Александровицем, было продублировано в [18, с. 64]. Однако у Гулда и Тобочника нет даже ссылки на статью Александовица. В то же время Александровиц ссылается в своей статье [1] на работу Лиса [8], поэтому говорить о независимости изложения алгоритма Александровицем вряд ли уместно. Судя по тому, что в работе Лиса [8] упоминается одна из ранних работ Хаммерсли с соавторами по перколяции узлов [3], Лис также мог быть знаком с идеями Хаммерсли.

Следует отметить, что в ряде работ алгоритм Лиса рассматривается как вариант модели кинетического роста (kinetic growth) [17, с. 139–174; 13], либо стохастического роста [16, с. 128–133, 206]. Далее сравниваются варианты описания и реализации алгоритма Лиса в публикациях [8; 1; 17; 11; 15]

Статья Лиса. Компьютерная программа использовала подпрограмму генерирующую псевдослучайные числа (называемую FLTRN в системе IBM в Ок-Риджской национальной лаборатории), чтобы случайным образом определить для каждого узла, занят он или нет. В отношении использованного языка программирования явных указаний в статье Лиса нет, однако, судя по тому, в каких системах программирования встречается подпрограмма FLTRN для реализации алгоритма Лис использовал язык программирования Fortran. Узел в начале координат (рис. 1) всегда считался занятым.

Затем программа шла наружу, по одной оболочке узлов за раз, случайным образом решая, были ли узлы свободными или занятыми, до тех пор, пока кластер узлов, соединенных через занятость ближайших соседей, не стал изолированным (т. е. до тех пор, пока вся оболочка из свободных или отключенных узлов не могла быть нарисована вокруг кластера). Каждый узел считался занятым (или нет) случайным образом с вероятностью  (или ), которая не зависит от занятости других узлов. Затем программа считала количество узлов в кластере, количество граничных узлов (включая внутренние границы) и среднеквадратичный размер (радиус гирации) кластера. Лисом были получены данные для 101086 кластеров при  и для 24310 кластеров при . Время выполнения было от  до  часов в каждом из двух случаев. [8]

Статья Александровица. В статье Александровица дается словесное описание алгоритма, но никаких технических указаний по поводу использовавшегося языка программирования нет. Для описания перколяционных кластеров используются критически разветвленные самоизбегающие блуждания (critically branched self-avoiding walks). Ветвление называется критическим, если оно достаточно, чтобы сделать вероятность выживания блуждания конечной на неограниченной длине. Берется решетка c координационным числом z, узлы которой могут быть заняты или пусты с вероятностью p и 1−p соответственно.

Согласно описанию Александровица, стохастический процесс производит блуждания, которые начинаются с занятого узла  и посещают один и только один раз узлы, связанные с  связями ближайших соседей, в данном микросостоянии решетки. В момент времени  процесса  соседей  становятся занятыми или пустыми, с (вероятностью)  и  соответственно. Пусть {} обозначает множество занятых узлов («концов ветвей») при конкретном выполнении процесса. В момент времени  все соседние с {} узлы, которые не посещались ранее (т. е. за исключением ), в свою очередь, становятся занятыми или пустыми, что дает множество {} вершин ветвления для  , и т.д., и т.п.

На каждом шаге конец ветви полностью окружается оболочкой узлов, назначаемых как занятые или пустые. По этой причине растущий конец избегает первых соседей по отношению ко всем узлам, занятым на предыдущих этапах процесса. Замкнутые петли могут образовываться, но только за счет встречи концов ветвей. [1]

Книга Гулда и Тобочника. Харви Гулд и Ян Тобочник отмечают, что алгоритм, предложенный Хаммерсли, Лисом и Александровицем, является наиболее эффективным способом генерирования обособленных перколяционных кластеров. [17] К сожалению, в русском переводе книги Гулда и Тобочника [17] есть неточности, поэтому дальнейшее описание алгоритма Гулда и Тобочника дается по [17] с уточнением по доступному черновику более позднего английского издания [4]. Гулд и Тобочник пишут, что алгоритм «роста» состоит из следующих шагов:

1. Занимается одна затравочная ячейка решетки. Четыре ближайших соседа (для квадратной решетки) образуют периметр затравочной ячейки.

2. Выбирается случайным образом ячейка периметра и генерируется случайное число . Если , то ячейка занимается, в противном случае она остается свободной. Чтобы ячейки были свободными с вероятностью , данная ячейка больше не проверяется.

3. Если ячейка занята, то определяется, нет ли новых ячеек периметра, т.е. непроверенных соседних ячеек.

4. Шаги 2 и 3 продолжаются до тех пор, пока не получится («не вырастет») кластер требуемого размера, или пока не останется непроверенных ячеек.

На рисунке приводится иллюстрация алгоритма по книге Гулда и Тобочника [17, с. 144]. Следует отметить, что Гулд и Тобочник используют немного специфическую терминологию и называют узлами периметра узлы роста, то есть непроверенные узлы, куда может вырасти кластер. Более корректно было бы называть данные узлы узлами роста периметра.

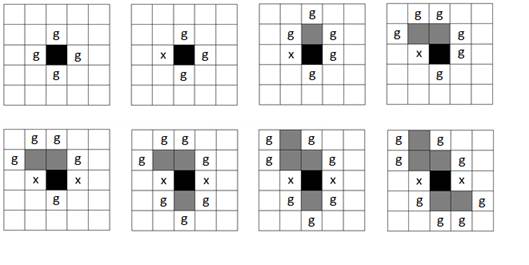
Рисунок. Пример «роста» перколяционного кластера. Затравочная ячейка - черный цвет, периметр - g, проверенные пустые ячейки - .

С технической точки зрения Гулд и Тобочник приводят примеры реализации алгоритма Лиса на двух языках программирования: языке True Basic и языке Pascal.

Статья Штауфера и Джана. Реализация программы близка к описанию Александровица. Используется список заполненных на очередном временном шаге  узлов (ячеек), на основе которого строится следующий слой заполненных узлов [11]. В статье приводится код реализации алгоритма на языке Fortran.

В отличие от реализации Гулда и Тобочника для роста кластера используется не случайно выбранная ячейка периметра, а проходятся все ячейки периметра, заполненные на предыдущем временном шаге. Особенность программы: используются спиральные граничные условия. При спиральных граничных условиях последний узел в строке считается соседним с первым узлом следующей строки.

Книга Алексеева. В книге Алексеева приводится реализация алгоритма Лиса на языке программирования Microsoft Visual Basic. В этом алгоритме рост кластера начинается с затравочной ячейки, располагающейся в центре решетки. Расположенные рядом ячейки — ближайшие соседи – образуют начальный периметр затравочной ячейки. Правило, по которому определяется понятие ближайших соседей, определяет геометрию решетки [15]. Программа близка к описанию Александровица. Особенностью программы является добавление анизотропии роста (по разным направлениям могут использоваться разные значения вероятности заполнения).

Заключение. В данной работе был проделан исторический экскурс в историю алгоритма Лиса и обсуждались разные варианты названия алгоритма. На наш взгляд предпочтительным является либо краткое название алгоритма как алгоритма Лиса, либо название по фамилиям трех авторов как алгоритма Хаммерсли-Лиса-Александровица. Также было проведено сравнение нескольких описаний и реализаций алгоритма Лиса и отмечены их различия.