ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕЗОНАНСОВ ПО ВЕЙВЛЕТ-ОБРАЗАМ СПЕКТРОВ ИЗЛУЧЕНИЯ ДЛЯ ГАУССОВЫХ ВЕЙВЛЕТОВ МЛАДШИХ ЧЕТНЫХ ПОРЯДКОВ

ESTIMATION OF RESONANCES PARAMETERS ON THE BASE OF THE WAVELET TRANSFORM OF RADIATION SPECTRA FOR GAUSSIAN WAVELETS OF THE SMALLEST EVEN ORDERS

Tatyana Podosenova

Candidate of Science in Physics and Mathematics, Senior Researcher, Lomonosov Moscow State University, Russia, Moscow

Аннотация. В работе предложен способ оценивания значений параметров резонансных линий в спектрах излучения, путем анализа полученных методом непрерывного вейвлет-преобразования вейвлет-образов спектров, с использованием гауссовых вейвлетов в качестве базовых. При получении аналитических оценок параметров использованы вычисленные в точках центров резонансов значения отношений вейвлет-коэффициентов, соответствующие базисным гауссовым вейвлетам двух разных порядков.

Abstract. The paper proposes a method for estimating the values of the parameters of resonance lines in the radiation spectra by analyzing the wavelet images of spectra obtained by the method of continuous wavelet transformation, by using of Gaussian wavelets as the base ones. When obtaining analytical estimates of the parameters, the values of the wavelets coefficients ratios corresponding to the basic Gaussian wavelets of two different orders are calculated at the points of the resonance centers.

Ключевые слова: спектр излучения; резонансная линия; непрерывное вейвлет-преобразование; гауссов вейвлет.

Keywords: radiation spectrum; resonance line; continuous wavelet transform; Gaussian wavelet.

1. Обработка исходных данных - аппаратно регистрируемых спектров излучения  - сводится в итоге к определению параметров суммы  резонансных унимодальных функций, в предположении нормального или по Пуассону закона распределения ошибок :

,                                    (1)

 ,  ,                                                       (2)

,  ,                                   (3)

,  ,   ,                                       (4)

где , ,  - центры, параметры полуширин и амплитуды пиков (резонансов), а  - гладкая базовая кривая.

2. В методе непрерывного вейвлет-преобразования, при выборе в качестве базисного вейвлета , коэффициенты вейвлет-разложения исходного спектра записываются в виде [1, с. 93]:

 ,                                                           (5)

где  - параметры масштаба и сдвига вейвлета. Для синглета  при выборе базисных гауссовых вейвлетов  2‑го и 4‑го порядков [1, с. 151], вейвлет-коэффициенты выписываются в явном виде [2]:

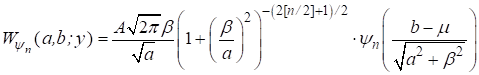 , ,       (6)

 ,  .                                 (7)

В работе используются также гауссовы вейвлеты , :

 ,  ,                                              (8)

 ,  .                                (9)

Отметим, что гауссовы вейвлеты  и  основаны на вычислении производных гауссовых функций,  и  соответственно [1, с. 151], и, конечно, различаются масштабами (полуширинами). Гауссовы вейвлеты симметричны относительно своего центра, поэтому локальные максимумы модулей коэффициентов вейвлет-разложения спектров совпадают с положениями одиночных резонансов. Графики функций  и  при четных значениях порядков  похожи формой на резонансные кривые, их аналитические представления можно записать через ортогональные полиномы Эрмита. А поскольку гауссовы вейвлеты имеют не менее двух первых нулевых моментов, они позволяют анализировать резонансные пики спектра без учета влияния достаточно медленной и плавной базовой компоненты спектра.

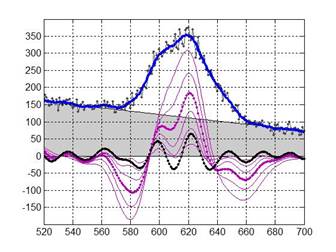
Рисунок 1. Графики кривых  и вейвлет-образов ,  зашумленного спектра  при различных масштабах вейвлетов:  при ,  при , 

3. Для гауссовых вейвлетов  при выполнении условия  справедливо: , . Поэтому для модулей  коэффициентов вейвлет‑разложения , вычисленных в точке центра синглета , справедливы соотношения:

,                                                                                 (10)

, ,

где . Оценки параметров синглета окончательно имеют вид:

,  .                               (11)

4. Для гауссовых вейвлетов  при значениях  выполняется: ,  [2]. И поскольку с точностью до линейного множителя базисные вейвлеты  совпадают с вейвлетами , то получим:

 ,

 ,

где  .

Окончательно формулы для оценивания параметров пика с использованием базовых гауссовых вейвлетов  имеют вид [2]:

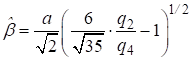,  ,                                (12)

 ,   ,

 ,  ,

где  .

5.  На модельных примерах протестируем качество предложенного алгоритма оценивания параметров синглетов. Алгоритм реализован в рамках системы компьютерной математики Matlab, на базе вейвлетов , включенных в пакет расширения Wavelet Toolbox [1, с. 135]. Рассмотрим синглет  с параметрами , , . Квазиреальные зашумленные спектры  будем формировать с учетом нормального (либо по Пуассону) закона распределения ошибок  (4):

 .                                                                         (13)

Затем квазиреальные спектры сгладим гауссовыми фильтрами, а полученные их вейвлет-разложения обработаем по алгоритму (п.4), на основе базисных вейвлетов . При фиксированном значении масштаба вейвлета за оценки положений центров резонансов возьмем аргументы точек локальных максимумов вейвлет-образов спектров.

В результате при значении масштаба вейвлетов , например, для невозмущенного модельного синглета были получены оценки параметров: , , а для двух зашумленных спектров  - оценки ,  и , .

Рассмотрим также случай, когда модельный спектр есть сумма базовой и резонансных компонент: , а базовая компонента спектра  задана в виде широкой гауссовой кривой с параметрами , , .

По описанному выше алгоритму при значении  для невозмущенного модельного спектра получены оценки , , а для двух зашумленных спектров - ,  и , .

Как следует из приведенных численных результатов, предложенный алгоритм оценивания параметров резонансных линий возможно использовать при решении задач обработки спектров излучения.