ОЦЕНКА ПАРАМЕТРОВ РЕЗОНАНСОВ ЧЕРЕЗ РАЗЛОЖЕНИЕ СПЕКТРОВ ИЗЛУЧЕНИЯ ПО ГАУССОВЫМ ВЕЙВЛЕТАМ 2-ГО ПОРЯДКА

ESTIMATION OF RESONANCES PARAMETERS THROUGH THE DECOMPOSITION OF RADIATION SPECTRA BY USING OF GAUSSIAN WAVELETS OF THE 2ND ORDER

Tatyana Podosenova

Candidate of Science in Physics and Mathematics, Senior Researcher, Lomonosov Moscow State University, Russia, Moscow

Аннотация. На основе метода непрерывного вейвлет-преобразования спектров, и с выбором гауссовых вейвлетов в качестве базисных, в работе получены аналитические выражения для оценок параметров полуширины и амплитуды резонансных линий. В формулах оценок используются вычисленные в точках центров резонансов значения отношений вейвлет-коэффициентов, полученных при разложениях спектра по двум различающимся параметрами масштаба гауссовым вейвлетам 2-го порядка. Описанные алгоритмы реализованы на языке системы компьютерной математики Matlab.

Abstract. By using of the continuous wavelet transformation of spectra and with the Gaussian wavelets as the base ones, the analytical expressions for estimating the parameters of the half-width and amplitude of resonant lines are considered in the paper. The formulas for the estimates use the values of the ratios of the wavelet coefficients which are calculated at the points of resonances centers. These coefficients are obtained as a result of the transformation of the spectra by two different Gaussian wavelets of the 2nd order corresponding to different scale values. The described algorithms are realized for the computer mathematics Matlab system.

Ключевые слова: спектр излучения; резонансная линия; непрерывное вейвлет-преобразование; гауссов вейвлет.

Keywords: radiation spectrum; resonance line; continuous wavelet transform; Gaussian wavelet.

1. Полученные в результате аппаратурных измерений спектры излучения рассматриваются в работе в виде суммы трех компонент - полезной, гладкой базовой и шумовой составляющих:

, ,                              (1)

где  - гладкая базовая кривая,  - шумовая компонента. В работе мы ограничимся гауссовой моделью формы резонансных линий:

,                                                                (2)

,  ,  ,                      (3)

где , ,  - центры, параметры полуширин и амплитуды линий спектра. В результате обработки исходных данных требуется оценить значения параметров , , , в предположении нормального или по Пуассону закона распределения ошибок :

,  ,   .                                       (4)

Оценивать параметры резонансов будем по вейвлет-образам спектров.

2. В методе непрерывного вейвлет-преобразования (НВП), при выборе в качестве базисного вейвлета , вейвлет-образ сигнала , а точнее, коэффициенты его вейвлет-разложения, записываются в виде [1, с. 93]:

,                    (5)

где  - базисная вейвлет-функция, а  - параметры масштаба и сдвига:

,  .                                  (6)

Вейвлет-преобразование сводится к вычислению корреляции между функциями  и фрагментами исходного сигнала.

Известно, что в силу коммутирования операции дифференцирования и НВП [2, с. 1155], для вейвлет-преобразований справедливы соотношения:

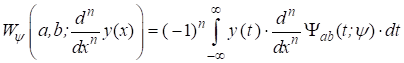 ,                                     (7)

что позволяет перейти от дифференцирования заданного численно исходного спектра  к дифференцированию выписываемого в виде аналитической функции вейвлета .

3. При преобразовании спектров методом НВП в работе в качестве базисных использованы гауссовы вейвлеты 2-го порядка -  и :

 ,  , ,       (8)

а при разметке спектров [3] - базисный гауссов вейвлет 4‑го порядка:

 ,  .                                (9)

Функции  и  вычисляются через производные гауссовых кривых  и  [1, с. 151]:

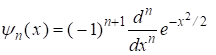,                                                                            (10)

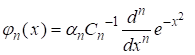, , , .                              (11)

Вейвлеты  и  используются в пакете расширения Wavelet Toolbox системы компьютерной математики Matlab [1, с. 135].

Доказано, что при выборе базисных гауссовых вейвлетов  2‑го и 4‑го порядков [1, с. 151], коэффициенты разложения синглета  выписываются в явном виде [3]:

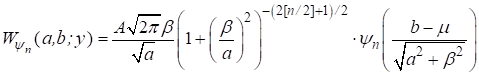 , .     (12)

Из формулы (12) следует, что рассматриваемые вейвлет-преобразования сохраняют положения одиночных резонансов на оси аргумента.

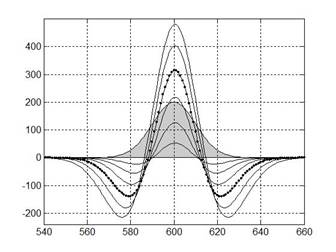
Рисунок 1. Графики синглета  и его вейвлет-образов  при различных масштабах вейвлетов: ,  

Важно отметить, что метод НВП на основе гауссовых вейвлетов, характеризующихся не менее чем двумя первыми нулевыми моментами [2], позволяет анализировать резонансные пики спектра без учета влияния медленно меняющейся базовой компоненты спектра. Графики используемых в работе базисных вейвлетов напоминают резонансные кривые (рис. 1).

4. Оценим полуширину синглета по двум его вейвлет-разложениям по гауссовым вейвлетам на основе  при двух различных значениях масштаба. При выборе  в качестве базисного вейвлета значение коэффициента разложения синглета  в точке , соответствующей центру пика, имеет вид [3]:

,  .                                           (13)

Нетрудно видеть, что при использовании различных масштабов  вейвлета, , будет справедливо равенство: , где , . Для простоты дальнейших выкладок введем обозначения: , . Тогда получим:

 ,      .

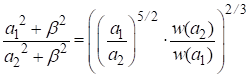Прологарифмируем последнее полученное соотношение:

.

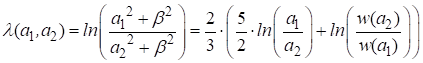И из равенства 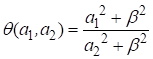, где , получим искомую оценку значения полуширины синглета:

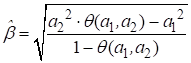.                                                                                  (14)

Оценки амплитуды пика  для значений масштабов  вейвлета в соответствии с формулой (13) будут иметь вид:

, .                                       (15)

5. Разберемся с оценкой параметров для случая базисного вейвлета . Известно, что с точностью до линейного множителя вейвлеты  совпадают с вейвлетами  [3], поэтому:

 ,

 .

Обозначим для простоты изложения через  значение коэффициента  разложения масштабированного синглета  в точке его центра [3], :  , где .

Поскольку, как предполагается, заданы разложения синглета для двух значений масштабов  вейвлета, , то справедливы равенства:

 ,

где , , и  ,  .

По аналогии с рассуждениями, проведенными выше (п.4), получим:

 ,   .

Прологарифмировав последнее из полученных соотношений:

 ,

и введя обозначение: , из равенства 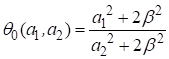 получим оценку значения полуширины синглета:

 .                                                                               (17)

Оценки амплитуды пика  будут иметь вид:

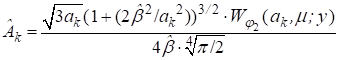, .                                     (18)

6. Вследствие численной неустойчивости операции дифференцирования, при обработке зашумленных данных обычно проводят предварительное сглаживание данных, например, гауссовыми фильтрами или сглаживающими полиномиальными фильтрами Савицкого-Голея (SG фильтрами) [4]. Сглаживание спектрометрических данных служит для уменьшения уровня шума в данных и, как следствие, ведет к снижению погрешностей анализа.

Сглаженные SG фильтрами значения спектра вычисляют по значениям локальных аппроксимирующих полиномов, полученных методом наименьших квадратов для точек спектра из соответствующего окна оси аргумента. Коэффициенты сглаживающего SG фильтра определяются только шириной окна сглаживания  и выбранным порядком полинома . Например, при обработке спектрометрических данных обычно достаточно использования сглаживающего кубического SG фильтра , который в этом случае задается квадратичным полиномом вида [4]:

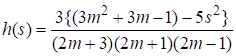,   .                                               (19)

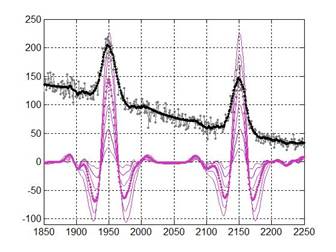
Рисунок 2. Графики зашумленного и сглаженного SG фильтром спектра  и вейвлет-образов  при различных масштабах вейвлетов: ,  

7. Рассмотрим возможности алгоритма оценивания параметров синглетов на примере. Алгоритм реализован в рамках системы компьютерной математики Matlab.

Модельный спектр, фрагмент графика которого показан на рис.2, задан суперпозицией 4-х гауссовых линий: ,- с параметрами , , , , базовая кривая  - суммой двух широких гауссианов. Зашумленный квазиреальный спектр смоделирован по закону распределения ошибок по Пуассону. В нижней части рис.2 точками выделен график кривой , соответствующей масштабу .

При обработке спектра положения центров резонансов  оценивались через абсциссы локальных максимумов кривой  [3]. Оценки полуширин  и амплитуд  пиков спектра вычислялись через выборочные медианы наборов оценок  и , полученных для базового гауссова вейвлета  при масштабах , . Разброс оценок этих параметров по отдельным резонансам можно проанализировать с помощью значений , , , , приведенных в таблицах 1-3. При обработке данных указанным алгоритмом заметно влияние точности указания центров пиков  на результаты работы алгоритма (см таблицы 2,3).

Таблица 1.

Обработка точных данных, 

Таблица 2.

Обработка сглаженных зашумленных данных 

Таблица 3.

Обработка сглаженных данных  при точно заданных значениях центров пиков

Как следует из приведенных численных результатов, предложенный алгоритм оценивания параметров резонансных линий возможно использовать при решении задач обработки спектров излучения.