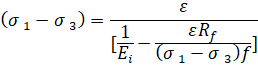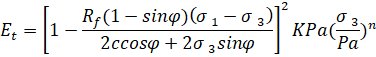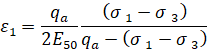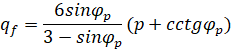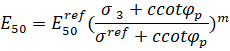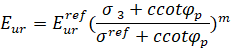ОБЗОР МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ГРУНТОВ, ПРИМЕНЯЕМЫХ В ГЕОТЕХНИЧЕСКОМ МОДЕЛИРОВАНИИ

OVERVIEW OF MATHEMATICAL MODELS OF SOILS USED IN

Ivan Sugonyaev

2nd year master's student, Tyumen Industrial University, Russia, Tyumen

Аннотация. В настоящее время при расчетах геотехнических конструкций часто применяются численные методики расчетов. В статье проводится обзор наиболее перспективной методики численного моделирования – модели упрочняющего грунта, Hardening soil model (HSM). Также в статье приводится небольшой обзор моделей, предшествующих Hardening soil model, на базе которых данная модель была разработана. Такие модели до сих пор применяются в отечественной практике при выполнении расчетов с применением численного моделирования. Наиболее глубокое понимание применения различных расчетных моделей в тех или иных ситуациях позволит увеличить надежность и понизить экономические показатели.

Abstract. Currently, numerical calculation methods are often used in the calculations of geotechnical structures. The article provides an overview of the most promising numerical modeling technique – the Hardening soil model (HSM). The article also provides a brief overview of the models preceding the Hardening soil model, on the basis of which this model was developed. Such models are still used in domestic practice when performing calculations using numerical modeling. The most in-depth understanding of the application of various calculation models in various situations will increase reliability and reduce the economic performance.

Ключевые слова. математические модели грунтов, численные расчеты, геотехническое строительство, модель Кулона–Мора, модель упрочняющегося грунта HSM, модель Дункана–Чанга.

Keywords. mathematical models of soils, numerical calculations, geotechnical construction, Coulomb–Mohr model, HSM hardening soil model, Duncan–Chang model.

В современном мире невозможно представить строительство зданий без привлечения компьютерных технологий, в том числе компьютерного моделирования. Так, например, для создания моделей грунтовых оснований применяются расчеты в основе которых лежат современные математические модели, основанные на линейном и нелинейном поведении грунтов [4, 8]. В большей степени начинают разрабатываться модели с применением механики дисперсных сред [1]. Современное численное моделирование геотехнических задач выполняется с помощью моделей, в основе которых лежат теория Фусса–Винклера (местных упругих деформаций) и упруго-пластическая теория, основанная на подходах Кулона–Мора, Друкера–Прагера [3]. Также современные инженеры применяют в своей практике модель упрочняющего грунта (HSM), в основе которой лежат модели Мора-Кулона и Дункана Чанга. Применение той или иной модели в каждом отдельном случае зависит от правильного понимания инженером  их сути, математического описания, а также их недостатков и преимуществ.

Модель Кулона–Мора. Данная модель описывает упругое поведение (рис. 3) и критерий прочности (рис. 1), при котором прочность на растяжение существенно меньше прочности на сжатие. Данная модель универсальна и используется в основе множества расчетных моделей, которые описывают поведение и прочность различных материалов [3, 5]. Данную модель предложил Ш. Кулон в XVIII в. В графическом варианте (рис. 2) модель отражает линейное разрушение и состоит из 2х прочностных характеристик: угла внутреннего трения - φ и удельного сцепления - С – удельное сцепление. Модель показывает зависимость между нормальными и касательными напряжениями.

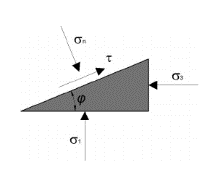
Рисунок 1. Схема действующих компонент напряжений на площадке

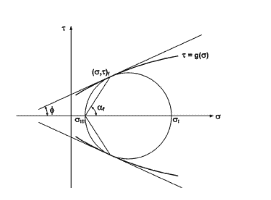
Рисунок 2. График критерия прочности Кулона–Мора

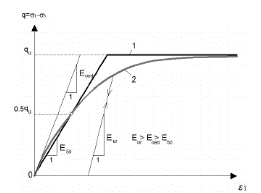
Рисунок 3. Графическое представление модели поведения Кулона–Мора:

1 – предельная поверхность по Кулону–Мору, 2 – реальное поведение грунта

Данная модель является одной из простейших и до сих пор применяется в численном моделировании.

Недостатком этой модели является постоянный модуль деформации на всем участке нагружения, при малых нагрузках – деформации завышены, при предельных нагрузках – деформации занижены.

Модель Дункана-Чанга. Нелинейная модель, которая не нашла применения в современных расчетах, это связано с несколькими недостатками.

Рисунок 4. Зависимость деформаций от напряжений

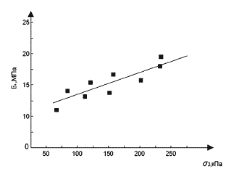
Рисунок 5. Изменение модуля деформации в зависимости от бокового давления

Но данная модель наряду с другими стала основой появления нелинейных моделей, в том числе модели HSM.

Во времена появления моделей с нелинейным характером зависимости деформаций от напряжений (рис. 4) была разработана гиперболическая модель Дункана-Чанга [6]. Модель имеет зависимость модуля деформации от напряжений (рис. 5):

После выполнения преобразований данное выражение получило вид:

где K – модульное число

 – атмосферное давление;

n – коэффициент, отражающий зависимость  от 

Модель Hardening soil model. Модель применяется при нелинейном поведении и разрушении грунта [9]. Для анализа деформированного состояния, данная модель учитывает 2 компоненты упрочнения – сдвиговую и объемную при изотропном нагружении (рис. 7) [11]. У HSM есть несколько преимуществ над ранее рассмотренной моделью Дункана-Чанга [9], благодаря:

1. Использованию шатрового механизма;
2. Изменению объема грунта (дилатансии);
3. Применению теории пластичности вместо теории упругости.

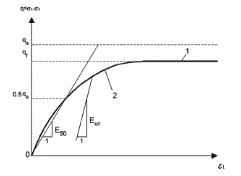
Рисунок 6. График изменения деформаций от девиаторного напряжения:

1 – гиперболическая функция,2 –предельная поверхность по Кулону–Мору

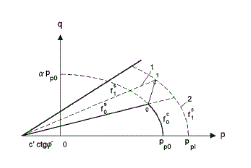
Рисунок 7. Область упрочнения модели HSM:

1 – упрочнение сдвига, 2 – объемное упрочнение

В основании модели лежит нелинейная зависимость деформаций от напряжений (рис. 6). С увеличением девиаторного напряжения, при деформировании грунта, происходит его упрочнение. Данное явление наблюдается с дренированным грунтом в условиях трехосного сжатия [7, 11]:

Где .

Закон упрочнения при изотропном нагружении, который отражает объемные деформации записывается в виде:

m – коэффициент отражающий изменение модуля упругости относительно напряжения [10].

 - модуль расширения/сжатия грунта.

Для того чтобы охарактеризовать деформации материала при первичном нагружении применяют секущий модуль деформации применяют параметр жесткости :

Для контроля развития пластических сдвиговых деформаций применяют модуль деформации референтный , для контроля при изотропном сжатии пластических деформаций применяют :

Модуль упругости применяют для ветви разгрузки, а также ветви повторного нагружения:

После чего производится расчет деформаций объема:

Угол дилатансии - 

Вывод. Аналитические методы, которые разработаны для ручного счета, поведение грунтов в которых является – линейным, отходят на второй план, и носят оценочный характер. Возможность использования современных математических моделей в расчетах, требует введения новых подходов на всех этапах строительства, увеличение нормативной базы, а также расширенного выполнения лабораторных исследований параметров грунтов.