МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОЕЗДА НА ПРЯМЫХ И КРИВЫХ В ПРОФИЛЕ УЧАСТКАХ ПУТИ

MATHEMATICAL MODELING TRAIN DYNAMICS ON STRAIGHT AND CURVED SECTIONS OF TRACK PROFILE

Nikita Komarovsky

postgraduate student, Belarusian State University of Transport, Belarus, Gomel

Аннотация. Основной целью исследования явлется оценка влияния кривизны пути в профиле на динамику подвижного состава. Для этого поставлены задачи: исследование факторов, оказывающих влияние на устойчивость движения грузовых поездов, а также выявление причин их поломок и повреждений. Создание математических моделей и алгоритмов, описывающих движение поездов с учетом специфики рельсового пути. Разработка математической модели, учитывающей расстояния между вагонами. Проведение теоретических исследований для оценки прочностных характеристик, устойчивости и динамических параметров движения при электродинамическом торможении, а также формулирование рекомендаций для повышения безопасности движения. Определение продольных динамических сил, действующих на грузовой поезд, основанное на экспериментальных данных, и сопоставление результатов с расчетными теоретическими и нормативными показателями. В ходе исследования были задействованы статические, аналитические и экспериментальные методы. Теоретические исследования основывались на принципах Даламбера, также использовалось программное обеспечение MSC Adams (автоматический динамический анализ механических систем). Эксперименты проводились как в лабораторных, так и в производственных условиях.

Abstract. The main purpose of the research is to assess the influence of track curvature in the profile on the rolling stock dynamics. For this purpose the following tasks are set: research of factors influencing the stability of freight trains, as well as identifying the causes of their breakdowns and damage. Creation of mathematical models and algorithms describing the movement of trains taking into account the specifics of the rail track. Development of a mathematical model that takes into account the distances between cars. Conducting theoretical studies to evaluate the strength characteristics, stability and dynamic parameters of motion under electrodynamic braking, as well as formulating recommendations to improve traffic safety. Determination of longitudinal dynamic forces acting on a freight train, based on experimental data, and comparison of the results with calculated theoretical and regulatory values. The study involved static, analytical and experimental methods. Theoretical studies were based on Dalembert's principles, and MSC Adams software (automatic dynamic analysis of mechanical systems) was also used. The experiments were carried out both in laboratory and production conditions.

Ключевые слова: торможение, подвижной состав, путь.

Keywords: braking, rolling stock, track.

В современном мире особое внимание уделяется созданию и совершенствованию конструкций железнодорожного подвижного состава для повышения их динамических характеристик и скорости движения, при этом обеспечивая безопасность и надежность. В развитых странах активно разрабатываются и моделируются локомотивы нового поколения с учетом таких параметров, как скорость, масса и длина, что позволяет достичь технико-экономической эффективности в их эксплуатации. Увеличение объемов грузовых и пассажирских перевозок на железнодорожном транспорте напрямую связано с устойчивой работой поездов в различных режимах. Поэтому важным аспектом является оптимальный выбор силы тяги и электродинамического торможения локомотива, а также снижение продольных динамических сил при движении поезда по наклонным участкам.

Научные исследования и технические работы в области проектирования подвижного состава сосредоточены на разработке и улучшении методов теоретических расчетов и экспериментальных исследований. Улучшение динамических характеристик и технико-экономических показателей является приоритетом в данной области. Таким образом, разработка рекомендаций по повышению динамических качеств и оценке продольных динамических сил, возникающих при движении грузового подвижного состава по различным участкам пути, а также обеспечение безопасности перевозок путем повышения устойчивости становится важной и актуальной задачей [1].

Математическая модель была реализована с использованием программного обеспечения MSC.ADAMS, что позволяет проводить оценку продольной динамики поезда в зависимости от массы, длины вагонов и расстояний между автосцепками. На этапе подготовки первоначальных данных и моделирования различных состояний сжатого или растянутого поезда есть возможность регулировать зазоры, что упрощает процесс расчетов и увеличивает их точность.

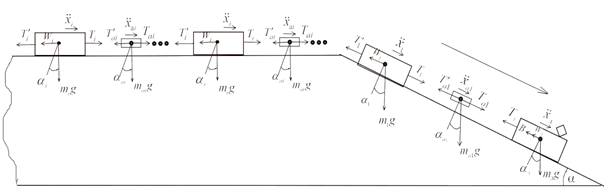
Рисунок 1. Схема спуска с уклона модели поезда с одним локомотивом

Согласно схеме, (рис. 1) математическое описание движения поезда выражается в виде системы уравнений равновесия [2-4]

                                                                            (1)

где m_л, m_аi, m_i – масса локомотива, автосцепок i-го межвагонного соединения и i-го вагона соответственно (i = 1, …, n); ,,  – продольные ускорения локомотива, автосцепок i-го межвагонного соединения и i-го вагона; W_л, W_i – основные силы сопротивления движению локомотива и i-го вагона; T_л, T_i, Tʹ_i – силы, действующие на поглощающие аппараты локомотива и i-го вагона; T_аi, Tʹ_аi – силы, действующие на автосцепные устройства i-го межвагонного соединения; B_л – сила электродинамического торможения и тяги локомотива; g – ускорение свободного падения; α_л, α_аi, α_i – уклон пути, по которому движется локомотив, автосцепки i-го межвагонного соединения и i-й вагон; n – количество вагонов в составе поезда.

Рисунок 2. Схема спуска с уклона модели поезда с двумя локомотивами

Математическое описание спуска поезда (рис. 2) согласно схеме выражается в виде следующей системы уравнений равновесия

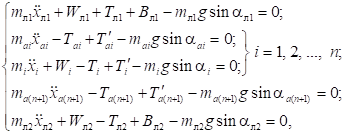                                                                           (2)

где m_л1, m_л2, m_аi, m_i, m_а(n+1) – масса локомотива, автосцепок i-го межвагонного соединения и i-го вагона соответственно (i = 1, 2, …, n); ,, , ,  – продольные ускорения локомотива, автосцепок i-го межвагонного соединения и i-го вагона; W_л1, W_i, W_л2 – силы основного сопротивления движению локомотива и i-го вагона; T_л1, T_л2 T_i, Tʹ_i – силы, действующие на поглощающие аппараты локомотива и i-го вагона; T_аi, Tʹ_аi, T _а(n+1), Tʹ_а(n+1) – силы, действующие на автосцепные устройства i-го межвагонного соединения; B_л1 B_л2 – сила электродинамического тормоза локомотива; g – ускорение свободного падения; α_л1, α_i, α_аi, α_л2, α_а(n+1) – уклон пути, по которому движется локомотив, автосцепки i-го межвагонного соединения и i-й вагон; n – количество вагонов в составе поезда.

В программном комплексе MSC Adams создана модель поезда (рис. 3), движущегося по прямому и наклонному пути. Локомотив и вагоны моделировались упрощенно, представляют собой твердые тела. Межвагонные соединения моделировались с использованием упруго-диссипативной связи, имитирующей работу автосцепного устройства.

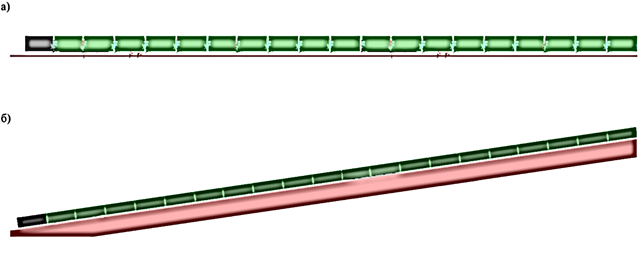
Рисунок 3. Компьютерная модель поезда в MSC ADAMS

Проверка, проведенная на основе теоретических исследований с использованием разработанной математической модели, показала высокую степень соответствия данных, полученных в результате экспериментов. Точность сравнения составила 97% между результатами исследования и расчетами, выполненными в программном обеспечении MSC.ADAMS.