ОБ ОСНОВНЫХ ПОНЯТИЯХ ТЕОРИИ ВЕРОЯТНОСТЕЙ, ПРИМЕНЯЕМЫХ В ТЕОРИИ ПЕРКОЛЯЦИИ

ON THE BASIC CONCEPTS OF PROBABILITY THEORY APPLIED IN PERCOLATION THEORY

Ivan Gordeev

Candidate of Sciences in Physics and Mathematics, Associate Professor in Astrakhan State University named after V.N. Tatishchev, Russia, Astrakhan

Boris Kasmynin

Student in Astrakhan State University named after V.N. Tatishchev, Russia, Astrakhan

Аннотация. В статье рассматриваются основные понятия теории вероятностей, которые используются во многих прикладных областях, в частности, при моделировании задач теории перколяции. Также дается сравнение различий в терминологии у разных авторов и расшифровываются некоторые злоупотребления обозначениями, встречающиеся в литературе по теории вероятностей. За основу для рассмотрения основных понятий были взяты публикации по теории вероятностей трех преподавателей МГУ: А.Н. Колмогорова, А.Н. Ширяева, А.В. Шкляева. Отмечены некоторые некорректности формулировок у указанных авторов.

Abstract. The article examines the basic concepts of probability theory, which are used in many applied areas, in particular, in modeling percolation theory problems. It also provides a comparison of the differences in terminology among different authors and deciphers some of the abuses of notation found in the literature on probability theory. The basis for examining the basic concepts were publications on probability theory by three Moscow State University teachers: A.N. Kolmogorov, A.N. Shiryaev, A.V. Shklyaev. Some incorrect formulations by these authors are noted.

Ключевые слова: теория вероятностей, вероятностное пространство, исход, элементарное событие, событие, алгебра событий, сигма-алгебра.

Keywords: probability theory, probability space, outcome, elementary event, event, algebra of events, sigma algebra.

Теория перколяции, применяемая для моделирования протекания в случайных средах, рассматривается в целом ряде монографий и статей, посвященных как общим теоретическим вопросам [10, 1], так и прикладным вопросам [3, 13, 2, 4, 6, 9, 8, 7]. С точки зрения математики, теория перколяции использует для моделирования теорию вероятностей и теорию графов.

В данной статье рассматриваются основные понятия теории вероятностей, которые используются во многих прикладных областях, в частности, при моделировании задач теории перколяции. Наряду с рассмотрением основных понятий дается сравнение различий в терминологии у разных авторов и расшифровываются некоторые злоупотребления обозначениями, встречающиеся в литературе по теории вероятностей. За основу для рассмотрения основных понятий были взяты публикации по теории вероятностей трех преподавателей МГУ: А.Н. Колмогорова [11], А.Н. Ширяева [15], А.В. Шкляева [16].

В теории вероятностей активно используются понятия «исход» и «событие». В книге Ширяева предлагается обозначать исходы буквой , добавляя к этой букве индекс, чтобы отличать разные исходы [15, с. 21]. Далее Ширяев предлагает называть исходы  элементарными событиями, а их совокупность

пространством элементарных событий или пространством исходов [15, с. 21]. Исходя из такого определения, можно считать, что понятие «исход» равносильно понятию «элементарное событие». Далее у Ширяева предлагается называть событиями все те подмножества  для которых по условиям эксперимента возможен ответ одного из двух типов: «исход » или «исход ». Мотивируя введение понятия «событие», Ширяев пишет, что обычно экспериментаторы «… интересуются не тем, какой конкретно исход имеет место в результате испытания, а тем, принадлежит ли исход тому или иному подмножеству всех исходов» [15, с. 27]. Исходя из сказанного Ширяевым, следует понимать слово «исход» как элемент, принадлежащий некоторому множеству событий, и соответственно слово «событие» следует использовать для множеств исходов, а слово «исход» для некоторого элемента множества. Здесь возникает интересный вопрос: следует ли считать элементарное событие событием? На самом деле, этот вопрос представляет интерес при рассмотрении множеств, состоящих из одного исхода. Вообще говоря, понятие множества , состоящего из одного элемента , не равносильно понятию этого элемента, но иногда в литературе этим различием пренебрегают. В литературе по теории вероятностей фраза «элементарное событие» иногда может пониматься как «исход », а иногда как «событие , состоящее из одного элемента (исхода) ». Ширяев старается употреблять термин «элементарное событие» только в значении «исход » и специально в отдельной таблице [15, с. 167] подчеркивает, что термины «исход» и «элементарное событие» в теории вероятностей соответствуют термину «элемент» в теории множеств.

Однако, у Ширяева в двух местах встречается фраза «пространство элементарных исходов» [15, с. 31, 37] и еще в одном месте встречается словосочетание «элементарных исходов» [15, с. 133]. Если термин «исход» строго соответствует термину «элементарное событие», то фраза «элементарный исход», по существу, является тавтологией.

В свою очередь, Колмогоров [11] практически не использует термин «исход», а предпочитает термин «элементарное событие».

Еще один преподаватель из МГУ, Шкляев А.В., наоборот, не использует словосочетание «элементарное событие», а всегда говорит об «исходах», хотя зачем-то во многих местах добавляет к слову «исход» прилагательное «элементарный», и фактически использует словосочетание «элементарный исход» как синоним слова «исход» [16].

Шкляев А.В. в лекциях по теории вероятностей приводит пример 8.3 [16, § 8.2], в котором строится множество , являющееся подмножеством полуинтервала  и удовлетворяющее двум условиям:

1. для любого  найдется такой элемент , что ;

2. для любых различных  величина .

Хотя Шкляев и не упоминает этого, но для  можно заметить, что поскольку , то, следовательно, и . Таким образом, в множестве  есть хотя бы одно рациональное число. Из второго условия следует, что в множестве  не может быть двух рациональных чисел, поэтому в множестве  должно быть одно рациональное число. Неформально можно сказать, что одно рациональное число  из  обслуживает все рациональные числа .

Для иррациональных чисел  можно заметить, что множество  должно содержать бесконечное подмножество иррациональных чисел. Для обоснования этого можно, например, рассмотреть бесконечное множество  иррациональных чисел, которые являются квадратными корнями из рациональных чисел (неизвлекающиеся хорошо: , , ,  и т.д.). Можно заметить, что разность любых двух различных иррациональных чисел такого вида тоже является иррациональным числом. Это можно показать от противного, допустим, . Тогда, берем правую и левую части и возводим их в квадрат , откуда . Тогда, отсюда следует, что число  является точным квадратом некоторого рационального числа, и можно представить  в виде несократимой дроби , где , а, откуда  или . Из последнего следует, что  должно делиться нацело на , но поскольку число  равно произведению двух простых множителей  и , то  должно делиться также на 2 и на 3, откуда следует, что  тоже должно делить на  и на , и, таким образом,  должно делиться на . Тогда существует , такое что  и , откуда . Но из последнего следует, что  и следовательно,  делятся на , и получается, что дробь  можно сократить на , что противоречит сделанному допущению. Соответственно, в множестве  должен быть элемент , такой что . Но для любого другого числа, например,  должен быть элемент , такой что . Можно показать, что , также используя метод от противного.

Допустим,  и . Вычитая  из , получаем , но выше было доказано, что .  является иррациональным числом, так как , а поскольку  и , то, следовательно, . Аналогично, . Таким образом, можно показать, что двум любым иррациональным числам  и , таким что , должны соответствовать разные числа  и . Таким образом получаем, что подмножество иррациональных чисел, принадлежащих  должно быть бесконечным.

Закончив предложенное здесь обоснование того, что множество иррациональных чисел, принадлежащих , должно быть бесконечным, можно возвратиться к выкладкам Шкляева. Шкляев предлагает далее пронумеровать все рациональные числа из интервала  (последовательными натуральными числами) и сконструировать множества , используя циклический сдвиг множества  на , такой что элемент  сдвигается в , если , или в , если  [16, с. 53]. Затем, Шкляев доказывает утверждение, что в случае  для множеств  и  выполняется . Для доказательства Шкляев показывает, что предположение о существовании числа  приводит к противоречию, поскольку тогда  и  (здесь имеется ввиду принадлежность в плане обратного циклического сдвига, т.е. если , то , аналогично для  и ). Если посмотреть разность  (возможно на единицу меньше или больше в случае перехода через границу), то эта разница оказывается рациональным числом, что противоречит второму условию для множества . Кроме этого, Шкляев пытается доказать, что . При доказательстве Шкляев утверждает, что для любого  найдется такое , что , а значит  [16, с. 54]. Это утверждение напоминает первое условие на множество , однако в первом условии на множество  нет явного указания на ограничение, что , но если , то это автоматически следует из того, что . Однако, возможен случай что , тогда утверждение Шкляева неверно, поскольку в этом случае . Также в первом условии на  возможен случай , но, возможно, Шкляев здесь предполагает циклический сдвиг с добавлением единицы, поскольку в этом случае . Таким образом, доказательство Шкляева можно считать корректным, если сделать оговорку что , и уточнить, что , когда , и , когда . В результате, по доказательству получится, что все  будут принадлежать одному из множеств  Дополнительно здесь следует заметить (Шкляев этого не делает), что для любого  выполняется  поскольку если существует , то либо  (когда ), либо  (когда ), но, по второму условию, множеству  не может принадлежать два разных элемента отличающихся либо на рациональное число , либо на рациональное число . Тогда  и , причем  являются семейством непересекающихся множеств.

Замечание. Для красоты определения можно добавить уточнение, что , тогда  для всех .

Кроме этого, Шкляев предлагает представить, что у каждого подмножества  полуинтервала  определена вероятность, причем так, что при циклическом сдвиге множества  на любое число  (т.е. элементы  из  переводятся в , если  и в , если ) вероятность множества не меняется. Затем Шкляев говорит, что обычная длина должна, казалось бы, удовлетворять этому свойству. Не совсем ясно, что имеет в виду Шкляев под обычной длиной, ведь обычная длина имеет смысл для непрерывных множеств, а рассмотренные выше множества  не являются непрерывными. Возможно, такой пассаж у Шкляева связан с тем, что множества  определяются у него после фразы про «обычную длину». Для множеств , которые не являются непрерывными, вместо «обычной длины» можно было бы говорить про некую «меру множества» наподобие меры Лебега. Однако, по построению, то, что описано Шкляевым, напоминает множество Витали, как оно описано в русской Википедии, но, согласно книге Секея [12, с. 195], такое множество было построено Цермело.

Поскольку множества  не пересекаются, то Шкляев замечает, зачем-то меняя индекс  на , что . В дальнейшем тексте Шкляев возвращается к обозначению , указывая что при этом все  одинаковы, а значит в правой части стоит ряд из одинаковых чисел и такой ряд может сойтись только если . Отсюда Шкляев делает вывод, что . Затем Шкляев опять возвращается к индексу , указывая, что , но тогда вероятность , и Шкляев называет этот результат противоречием. На самом деле, чтобы действительно говорить о противоречии, надо также добавить, что  равно нулю, как и все остальные  и рассматривать вероятность объединения всех множеств с индексами от нуля до бесконечности, т.е. . Таким образом, нельзя построить непротиворечивую вероятностную меру на всех подмножествах  с простым свойством однородности относительно сдвигов, и приходится выделять такие множества подмножеств элементарных событий, из которых исключены некоторые «нехорошие» подмножества.

При рассмотрении общего вероятностного пространства прежде всего вводится пространство элементарных исходов , представляющее собой некоторое множество, на которое не накладывается ограничений.

Необходимостью исключения «нехороших» подмножеств Шкляев мотивирует введение сигма-алгебры событий , которая представляет собой множество некоторых подмножеств пространства элементарных исходов , удовлетворяющее следующим условиям:

1. ;

2. Если , то , где дополнение  рассматривается до ;

3. Если  принадлежат , то множество

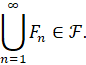
С использованием сигма-алгебры событий Шкляев дает определение вероятностной меры  [16, с. 52]: отображения из сигма-алгебры  подмножеств пространства элементарных исходов  в отрезок , которое удовлетворяет следующим свойствам:

1. ;

2. аддитивность:  при любых непересекающихся  из ;

3. счетная аддитивность:

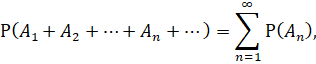
где  – произвольные непересекающиеся множества, принадлежащие .

У Шкляева в последнем условии для вероятностной меры вместо «множества, принадлежащие », говорится «подмножества » [16, с. 52], что некорректно, поскольку  является элементом , а не подмножеством .

Можно заметить, что проблема с множествами Витали возникает только при попытке определить вероятностную меру как некую «длину», для которой допускается сдвиг множества на любое число  с сохранением вероятностной меры. Тот же Шкляев приводит пример вероятностной меры, корректно определенной на пространстве элементарных исходов  и множестве всех его подмножеств , пример 8.1 [16, с. 52]. В этом примере Шкляев определяет вероятностную меру для любого множества : , где  – число точек вида , , в множестве . Шкляев показывает, что все условия, необходимые для вероятностной меры, при таком определении выполняются, и, следовательно, тройка  образует вероятностное пространство. Однако, сохранение вероятностной меры при сдвиге множества  на любое число  в общем случае не будет выполняться, здесь сохранение вероятностной меры происходит только при циклическом сдвиге на рациональные числа вида , где . Таким образом, проблемы возникают только при сочетании некоторых сигма-алгебр  с некоторыми способами определения вероятностной меры.

Ширяев [15], во избежание недоразумений, говорит про конечную аддитивность там, где Шкляев говорит просто про аддитивность. Кроме этого, Ширяев уточняет, что конечно-аддитивная мера  заданная на алгебре  подмножеств множества , называется счетно-аддитивной (–аддитивной) или просто мерой, если для любых попарно непересекающихся множеств  из  (у Ширяева опечатка, вместо  написано ) таких, что  [15, с. 163],

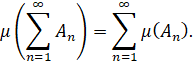
Далее, Ширяев говорит, что счетно-аддитивная мера  на алгебре , удовлетворяющая условию , называется вероятностной мерой или вероятностью (определенной на множествах алгебры ) [15, с. 164].

Можно заметить, что здесь Ширяев использует понятие просто алгебры , а не сигма-алгебры . Следует отметить, что Ширяев почему-то дает два разных определения алгебры, одно определение в первой главе, посвященной конечным пространствам  элементарных событий [15, с. 28], и другое в второй главе, посвященной бесконечным пространствам  элементарных событий [15, с. 162]. В первом определении, хотя Ширяев не оформил его словом «определение», Ширяев называет алгеброй такую систему  подмножеств множества , что

1) ,

2) если , , то множества  также принадлежат .

Это определение алгебры практически совпадает с определением алгебры множеств у Колмогорова [11, с. 10], который называет алгеброй систему  подмножеств множества , если , соединение, пересечение и разность двух множеств опять принадлежат системе . Отличие определений заключается в букве, которую использовали для обозначения алгебры (у Ширяева , у Колмогорова ), а также в том, что Колмогоров в определении вместо символических обозначений для операций с множествами использует словесные названия этих операций (соединение, пересечение и разность). Немного отличается у Колмогорова также название одной из операций: Колмогоров предпочитает говорить о соединении множеств, а Ширяев об объединении множеств. Далее, Колмогоров использует данное определение алгебры и для бесконечных пространств  элементарных событий.

В то же время, Ширяев почему-то дает еще одно определение понятия алгебры для бесконечного пространства  следующим образом [15, с. 162]:

Пусть  – некоторое множество точек . Система  подмножеств  называется алгеброй, если

a) ,

b) ,

c) .

Ширяев отмечает, что в условии b) достаточно, чтобы выполнялось либо , либо , так как ,  [15, с. 162]. Отличие второго определения Ширяева от первого заключается в том, что в первом определении используется понятие разности множеств, а во втором определении используется понятие дополнения множества.

Можно посмотреть, являются ли эти определения по существу разными. Здесь можно отметить, что Колмогоров называет «дополнительным множеством» и определяет его через разность , в то время как Ширяев предпочитает название «дополнение». Если исходить из первого определения, то поскольку  и , и, по определению, , то дополнение , таким образом, из первого определения следует второе. Если исходить из второго определения, то поскольку ,  и , то . Аналогично можно показать, что , и таким образом из второго определения следует первое. К сожалению, Ширяев не дает никаких пояснений о том, зачем ему понадобилось второе определение, отличающееся от определения Колмогорова.

Ширяев вводит также понятие сигма-алгебры, определяя ее как систему , и для которой выполняется дополнительное свойство:

Если , то

при этом достаточно, чтобы либо , либо .

Данное определение Ширяев дает как раз, переходя к рассмотрению вероятностных моделей, описывающих эксперименты типа бесконечного подбрасывания монеты [15, с. 161], которые как раз и соответствуют перколяционной модели, где пронумерованы ребра либо узлы. Ширяев также отмечает, что в данном случае приходиться иметь дело с несчетным пространством  [15, с. 162]. При этом, пространство  определяется у Ширяева как

Ширяев, отмечая, что всякое число  можно однозначно разложить в содержащую бесконечное число нулей двоичную дробь, в виде

делает вывод, что между точками  пространства  может быть установлено взаимно однозначное соответствие и, значит, мощность множества  равна мощности континуума. Упоминание о бесконечном количестве нулей в двоичной дроби, по-видимому, связано с тем, что для действительного числа , в котором содержится конечное число нулей, начиная с некоторого разряда  все цифры будут единицами (последний нулевой разряд ), а такие действительные числа, с точки зрения разложения в геометрическую прогрессию, считаются эквивалентными числам, в которых разряд  заменен на единицу, все следующие разряды, начиная с , заменены нулем, а разряды перед  такие же. Например, число  считается эквивалентным числу . Однако, с точки зрения событий  и  это существенно разные события, в одном из которых почти всегда выпадала единица, а в другом почти всегда выпадал ноль. Возможно, Ширяев просто пренебрегает этим отличием  и , поскольку множество событий

однозначно соответствуют некоторому бесконечному подмножеству рациональных чисел, и таким образом счетно, а каждому элементарному событию  можно поставить взаимно однозначное соответствие элементарное событие , где

и, таким образом, множество  тоже счетно. В тоже время, в теории множеств известна теорема, что объединение бесконечного множества  со счетным множеством  имеет такую же мощность что и множество  [5, с. 16-17], поэтому  равномощно .

Вероятностным пространством называется тройка , состоящая из пространства элементарных исходов , определенной на множестве  сигма-алгебры событий , и определенной для сигма-алгебры  вероятностной меры  [16, с. 52]. Аналогичное определение вероятностного пространства как тройки  есть и у Ширяева [15, с. 166]. Однако, Ширяев вводит также понятие измеримого пространства, которое представляет собой пару , где  – некоторое пространство, а  – сигма-алгебра его подмножеств [15, с. 163].

Некоторая странность определения у Ширяева заключается в том, что в определении вероятностной меры (вероятности) Ширяев говорит о счетно-аддитивной мере  на алгебре , удовлетворяющая условию , т.е. не требует, чтобы алгебра  обязательно была сигма-алгеброй [15, с. 164]. Возможно, у Ширяева просто пропущено в определении вероятности, что алгебра  является сигма-алгеброй, либо Ширяев допускает рассмотрение вероятностей не на сигма-алгебре, но конкретных примеров такого рассмотрения вероятности не приводит.

В целом, у Ширяева многие моменты изложены несколько подробнее. В частности, Ширяев говорит о «богатстве» сигма-алгебр, определенных на пространстве  элементарных событий, отмечая, что  и  являются и алгебрами, и сигма-алгебрами, причем  самая «бедная» сигма-алгебра, а  – самая «богатая» сигма-алгебра [15, с. 171]. Также Ширяев вводит понятие алгебры, порожденной множеством , определяя такую алгебру как систему множеств:

и отмечает, что данная алгебра является также сигма-алгеброй [15, с. 171]. Здесь не совсем ясно, зачем Ширяев говорит о сигма-алгебре, ведь понятие сигма-алгебры актуально в случае, когда система рассматриваемых в алгебре множеств является бесконечной, а в алгебре  всего четыре множества. Далее Ширяев рассматривает системы множеств, порождаемые счетными разбиениями пространства элементарных событий  на непустые множества. Для разбиения Ширяев вводит обозначение

где  и . Система , образованная из множеств, являющихся объединением конечного или счетного числа элементов разбиения (с присоединенным пустым множеством), является алгеброй (и сигма-алгеброй). Также Ширяев приводит лемму, согласно которой для любых множеств  из  существуют наименьшая алгебра, обозначаемая , и наименьшая сигма-алгебра, обозначаемая , содержащие все множества из  [15, с. 171]. Соответственно, систему  (или ) называют (наименьшей) алгеброй (сигма-алгеброй), порожденной системой множеств .

Для установления того, что заданная система множеств является сигма-алгеброй Ширяев вводит понятие монотонного класса. Система  подмножеств  называется монотонным классом, если из того, что , и  или , следует, что  [15, с. 172]. Здесь  означает, что   означает, что  и . В свою очередь,  означает, что   означает, что  и  [15, с. 519].

Далее Ширяев формулирует лемму [15, с. 172], согласно которой, для того чтобы алгебра  была в тоже время и сигма-алгеброй, необходимо и достаточно, чтобы эта алгебра была монотонным классом. Также, Ширяев вводит обозначение для наименьшего монотонного класса , содержащего систему множеств , но к сожалению не дает определения, какой монотонный класс называется наименьшим. Данный пробел восполняется в литературе по теории вероятностей, например, определение наименьшего монотонного класса встречается в сборнике задач у Дороговцева и др. [14, с. 8]. Согласно определению в данном сборнике задач, если  является некоторым классом подмножеств , то наименьший монотонный класс  – это монотонный класс, для которого каждое множество из  принадлежит  и какой бы ни был монотонный класс , содержащий ,

.

В обозначениях у Ширяева [15] по сравнению с Дороговцевым и др. [14], имеются небольшие отличия: в [15] используется для нестрого включения знак «», в то время как в [14] используют для нестрого включения знак «». Также в формулировках в [15] и в [14] есть небольшое отличие: в [15, с. 171] говорится о системе множеств , а в [14, с. 8] говорится о классе множеств . По-видимому, Ширяев употребляет фразы «система множеств» и «класс множеств» как синонимы, поскольку, например, Ширяев сначала говорит о системе подмножеств , а затем говорит о той же системе подмножеств  как о классе всех подмножеств пространства  [15, с. 171]. Аналогично у Дороговцева и др. фразы «система подмножеств» и «класс подмножеств» используются как синонимы, например, в задании I.1.26 говорится о классе подмножеств, а в задании I.1.27 в аналогичной ситуации говорится о системе подмножеств [14, с. 7].

Также Ширяев доказывает теорему о том, что для любой алгебры  выполняется

т.е. наименьший монотонный класс и наименьшая сигма-алгебра, включающие алгебру  совпадают. Далее Ширяев дает определение -систем и -систем множеств [15, с. 175]. Согласно Ширяеву, система  подмножеств  называется -системой, если она замкнута относительно взятия конечных пересечений: если , то , а система  подмножеств  называется -системой, если

a) ,

b) ,

c) .

Ширяев также отмечает, что в определении -системы можно заменить пару условий b) и c) на другую пару условий:

d) если , то ,

e) если  для , то .

Здесь можно заметить, что Ширяев злоупотребляет обозначением . В свойстве c) записано, что . По-видимому, запись  следует читать как запись, сделанную в определении сигма-алгебры,  Однако, остается вопрос, что означает запись ? Вероятно, такое злоупотребление записью характерно для литературы по теории вероятностей, поскольку подобные записи встречаются и в [14], например, в определении сигма-алгебры [14, с. 3]. К счастью, у Дороговцева и др. кое-где встречаются расшифровки, поясняющие обозначение . Например, в задаче I.1.6 написано «пусть  – последовательность множеств» [14, с. 4]. В других задачах встречаются другие пояснения. Так в задаче I.1.10 встречается пояснение «пусть  – некоторая последовательность подмножеств » [14, с. 5]. Здесь  взято в фигурные скобки, которые подчеркивают, что речь идет не об одном элементе из последовательности, а обо всей последовательности и кроме того, в пояснении уточняется, что  является подмножеством . Уточнение о принадлежности  множеству  в большинстве случаев опускается, но, по-видимому, неявно подразумевается. К сожалению, Дороговцев и др. тоже в большинстве случаев пренебрегают употреблением фигурных скобок и уже в задачах I.1.12 и I.1.13 пишут «пусть  – последовательность подмножеств ». В тоже время, когда в [14] употребляется запись , то почему-то не уточняется, какие значения может принимать , хотя такое уточнение разумно и при использовании фигурных скобок. Запись  означает, что  принимает значения, являющиеся последовательными натуральными числами, и многоточие в конце означает, что используется сколь угодно большие натуральные числа, т.е. последовательность  является бесконечной последовательностью множеств, пронумерованных натуральными числами, причем для любого значения  выполняется . Из того, что элементы бесконечной последовательности множеств пронумерованы натуральными числами, следует что эта последовательность  сама является счетным множеством. В последней фразе как раз видно, насколько важно употребление фигурных скобок, когда речь идет о всей последовательности, чтобы отличать это от случая, когда речь идет об элементе последовательности, который в свою очередь является множеством, поскольку элемент последовательности множеств в свою очередь может быть счетным множеством. У Шкляева в свою очередь, встречается очень интересный вариант записи « принадлежат » [16, с. 53], который означает, что рассматривается бесконечная последовательность множеств  и каждый элемент этой последовательности, обобщенно обозначаемый , принадлежит . Запись Шкляева, по существу, близка к записи Дороговцева и др. « – последовательность подмножеств » [14, с. 5], где Дороговцев и др. также вводят обобщенное обозначение члена бесконечной последовательности , при этом явно употребляется слово «последовательность», а ее бесконечность подчеркивается заданием правила для индекса , который является обобщенным обозначением элемента бесконечной последовательности . Более корректной записью, по сравнению с записью «», была бы запись «». Последняя запись является более корректной, поскольку она подчеркивает, что запятую, которая стоит после единицы, не следует рассматривать как завершение формулы . Если посмотреть определение сигма-алгебры в [14, с. 3], то можно увидеть запись «», напоминающую запись в пункте c) у Ширяева [15, с. 175]. Соответствующую запись у Дороговцева и др. следует читать как «рассматривается бесконечная последовательность множеств, где , и каждый элемент этой последовательности, обобщенно обозначаемый , принадлежит ». Соответственно, запись Ширяева «», по-видимому, следует читать аналогично: «рассматривается бесконечная последовательность множеств , где , и каждый элемент этой последовательности, обобщенно обозначаемый , принадлежит ». Далее в формулировке свойства c) у Ширяева встречается запись , которая означает, что рассматривается монотонная последовательность множеств , .

Однако, в пункте e) Ширяев еще больше злоупотребляет обозначениями, записывая « для ». Первая часть этой записи «» была расшифрована выше, но возникает вопрос что означает вторая часть записи « для »? Наибольшую странность в этой записи имеет способ задания , для которого сказано только, что  не равно . Если расшифровать вторую часть записи, то, по-видимому, ее следует читать как «для любых , когда  выполняется ».