Прямая и обратная задача теории рассеяния для возмущенного оператора Штурма-Лиувилля
Конференция: XXXI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Секция: Вещественный, комплексный и функциональный анализ

XXXI Международная научно-практическая конференция «Научный форум: технические и физико-математические науки»
Прямая и обратная задача теории рассеяния для возмущенного оператора Штурма-Лиувилля
Аннотация. В данной работе решается прямая и обратная задачи теории рассеяния для возмущенного оператора Штурма-Лиувилля, т.е. находятся необходимые условия на набор величин при которых они служили бы, данными рассеяния заданного оператора, затем доказывается достаточность этих условий.
Ключевые слова: Уравнение Штурма-Лиувилля; Теория рассеяния; Обратная задача, оператор преобразования, равенство Парсеваля.
1. Введение. Есть несколько версий обратной задачи Штурма-Лиувилля. Первые важные результаты в этом направлении, были получены [1]. Интерес к обратным задачам возрос из-за связей обратных задач с некоторыми важными нелинейными уравнениями математической физики. Подробное изложение связей обратных задач с нелинейными уравнениями (не только Кортефега – де Фриза) посвящена монография В.Е.Захарова, С.В.Манакова. В настоящее время, обратные задачи изучаются для некоторых специальных классов обыкновенных дифференциальных операторов. Эффективный метод построения регулярного и сингулярного оператора Штурма-Лиувилля по спектральной функции или по двум спектрам дается [2, 3, 4]. Детали обратных задач для сингулярных уравнений были приведены в [5, 6,] и в ссылках в них. Следует отметить, что в процессе эффективного решения обратных задач рассеяния оператор преобразования с условиями на бесконечности открытый Б.Я.Левиным играет важную роль. Принципиальным моментом здесь является построение оператора преобразования с условиями на бесконечности, переводящего решение невозмущенного уравнения ![]() в решение возмущенного уравнения
в решение возмущенного уравнения ![]() , при условии
, при условии
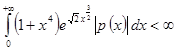 (1)
(1)
Доказывается, что ядро ![]() (8) оператора преобразования является решением граничной задачи (9)-(10). Методом Римана доказывается, что для решения граничной задачи (9)-(10) достаточно интегральное уравнение (14). Применяя метод последовательных приближений, доказывается единственность решения этого уравнения. С помощью оператора преобразования находим асимптотику нормированных собственных функций граничной задачи
(8) оператора преобразования является решением граничной задачи (9)-(10). Методом Римана доказывается, что для решения граничной задачи (9)-(10) достаточно интегральное уравнение (14). Применяя метод последовательных приближений, доказывается единственность решения этого уравнения. С помощью оператора преобразования находим асимптотику нормированных собственных функций граничной задачи
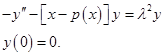
Далее выводится и исследуется основное интегральное уравнение (17) для ядра ![]()
2.Равенство Парсеваля для ![]() .
.
В случае ![]() можно показать, что функция
можно показать, что функция
 (2)
(2)
является решением уравнения
![]() (3)
(3)
и ![]() при
при ![]() - цилиндрические функции Ганкеля.
- цилиндрические функции Ганкеля.
Обозначим через ![]() решение уравнения (3), удовлетворяющее условиям
решение уравнения (3), удовлетворяющее условиям
![]() (4)
(4)
Используя формулу (2) доказываем,что
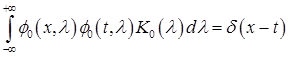 (5)
(5)
где
 (6)
(6)
3.Оператор преобразования с условием на бесконечности.
Здесь мы находим условия существования оператора преобразования типа, введенным Б.Я.Левиным.
Теорема. Пусть выполняется условие (1). Тогда при любом ![]() уравнение
уравнение ![]() имеет решение
имеет решение ![]() с условием
с условием
![]() (7)
(7)
и существует ядро ![]() такое, что
такое, что
 (8)
(8)
где ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
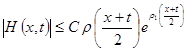 (12)
(12)
и
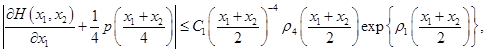 (13)
(13)
где
![]()
4. Разложения по собственным функциям оператора ![]() .
.
Обозначим через ![]() решение уравнения
решение уравнения ![]() удовлетворяющее условиям (4). Мы доказываем справедливость существования разложения:
удовлетворяющее условиям (4). Мы доказываем справедливость существования разложения:
![]() (14)
(14)
где ![]() . Таким образом, функция
. Таким образом, функция
![]()
является нормированной собственной функцией непрерывного спектра оператора ![]() .
.
Введя обозначение ![]() мы замечаем, что для вещественных значений
мы замечаем, что для вещественных значений ![]()
![]() (15)
(15)
![]() (16)
(16)
Из этой формулы следует, что при ![]() асимптотическое поведение
асимптотическое поведение ![]() определяется функцией
определяется функцией ![]() . Эту функцию мы назовем функцией рассеяния оператора
. Эту функцию мы назовем функцией рассеяния оператора ![]() .
.
Лемма 1. Функция рассеяния ![]() определена на всей вещественной оси, унитарна:
определена на всей вещественной оси, унитарна:
![]() и
и ![]()
Лемма 2. Интегральное уравнение
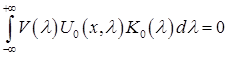
имеет лишь тривиальное решение в ![]()
![]()
5. Основное уравнение для ядра ![]() .
.
Умножим обе части равенство (15) на ![]() и проинтегрируем по параметру
и проинтегрируем по параметру ![]() от
от ![]() до
до ![]() .
.
Используя равенство Парсеваля (14) после элементарных преобразований мы получим основное интегральное уравнение типа В.А.Марченко:
![]() (17)
(17)
где
 (18)
(18)
![]()
функцию ![]() будем называть функцией перехода. Она играет важную роль при решении обратной задачи.
будем называть функцией перехода. Она играет важную роль при решении обратной задачи.
Лемма 3. Функция перехода ![]() удовлетворяет неравенству
удовлетворяет неравенству
![]() (18')
(18')
и непрерывные частные производные ![]() удовлетворяют неравенству
удовлетворяют неравенству
![]() , (19)
, (19)
где ![]() убывающая и интегрируемая функция на
убывающая и интегрируемая функция на ![]() .
.
Доказательство.
Для доказательства применим основное уравнение (17) и оценку (12). В основном уравнении (17) возьмем функцию ![]() в качестве неизвестного. Тогда для функции
в качестве неизвестного. Тогда для функции ![]() получим уравнение
получим уравнение
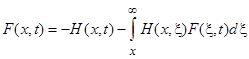
Возьмем
![]()

Учитывая оценку (12), имеем
![]()


![]()
Следовательно, ![]() . Методом математической индукции доказывается, что
. Методом математической индукции доказывается, что ![]() ,
, ![]() .
.
Следовательно, ряд  , сходится равномерно в области
, сходится равномерно в области ![]() , и функция
, и функция ![]() является решением основного уравнения, и для него справедливы оценки (18').
является решением основного уравнения, и для него справедливы оценки (18').


