ПРИМЕНЕНИЕ CAE МОДЕЛИРОВАНИЯ ДЛЯ АНАЛИЗА ПРОЦЕССА РЕЗАНИЯ

APPLICATION OF CAE SIMULATION FOR ANALYSIS OF THE CUTTING PROCESS

Alexey Pakhomov

PhD Student, Moscow State University of Technology "STANKIN", Russia, Moscow

Аннотация. Данная статья посвящена проблеме применения технологий компьютерного инжиниринга (CAE) для моделирования и анализа процесса резания металлов. Основное внимание автор уделяет использованию программного комплекса Abaqus / CAE для предсказания сил резания, тепловых полей, зон повреждений и других критически важных параметров. В работе обоснована значимость CAE-подхода при проектировании режущего инструмента и выборе режимов его обработки, что позволяет существенно сократить затраты на физические испытания. Приводятся примеры из научной литературы и результаты собственной симуляции ортогонального точения. Описана методология задания условий моделирования, включая расчетную сетку, начальные и граничные условия, а также использование критерия Джонсона–Кука для характеристики пластичности материала и эволюции повреждений. Представлены графики температурных распределений, полей напряжений и повреждений. Обоснована применимость различных типов моделей (2D и 3D) в зависимости от целей исследования. Результаты проведенной научной работы демонстрируют практическую ценность при прогнозировании износа, повышении стойкости инструмента и оптимизации режимов резания.

Abstract. The article examines the application of Computer-Aided Engineering (CAE) technologies for simulating and analyzing the metal cutting process. The primary focus is on using the Abaqus/CAE software suite to predict cutting forces, thermal fields, damage zones, and other critical parameters. The significance of the CAE approach in designing cutting tools and selecting machining parameters is substantiated, as it enables a significant reduction in the costs associated with physical testing. Examples from the literature and results from the author's own orthogonal turning simulation are presented. The methodology for defining simulation conditions is described, including the finite element mesh, initial and boundary conditions, as well as the use of the Johnson-Cook criterion to model material plasticity and damage evolution. Graphs illustrating temperature distributions, stress fields, and damage fields are presented. The applicability of different model types (2D and 3D) depending on research objectives is justified. The results demonstrate the practical value of this approach for predicting tool wear, increasing tool life, and optimizing cutting parameters.

Ключевые слова: CAE-моделирование; Abaqus; модель Джонсона—Кука.

Keywords: CAE simulation; Abaqus; Johnson–Cook model.

Введение. Современное CAE-моделирование позволяет подробно ана-лизировать процесс резки металлов, моделируя основные деформационные зоны и связанные с ними поля температур и напряжений. Можно определить следующие рабочие зоны рассматриваемого процесса:

• первичную зону – в материале у режущего лезвия;
• вторичную зону – на поверхности инструмента вследствие трения;
• третичную зону – позади режущей кромки.

Использование CAE в резании особенно оправдано при работе с труднообрабатываемыми материалами, для которых характерны низкая удельная теплопроводность и высокие силовые нагрузки, а проведение физических экспериментов является дорогостоящим и сложным.

Преимущества CAE-моделирования включают в себя:

• Прогнозирование дефектов, позволяющее выявить образование трещин и задиров в материале, оптимизировать режимы резки: скорости, подачи, охлаждения и подобрать оптимальные инструментальные материалы [4], [5].
• Анализ температурных полей и распределения сил – это возможность провести изучение без множества физических испытаний, позволяя снизить затраты на эксперименты на 40–60 % [7].
• Адаптация к новым материалам и сложным геометриям заготовок. Численные модели могут быстро настраиваться для исследования новых материалов и обработки деталей с нестандартной формой.

Например, исследования [1] показали, что включение модели накопления повреждений в расчёты увеличивает прогнозируемые силы резки и остаточные напряжения, приближая результаты симуляции к экспериментальным. В литературе [2] также приводятся примеры верификации CAE моделей для резания композитных материалов.

• Цель исследования: исследовать моделирование, заключающиеся в нем вводные данные и уравнения.

Для моделирования процесса резки задаются физические параметры и закономерности. В частности, вводится безразмерная температура:

 ,                                                                                                     (1)

где  ​ – температура окружающей среды,

​ – температура плавления материала.

Нормализация подобного рода позволяет масштабировать текущую температуру по шкале от 0 (комната) до 1 (плавление).

Для описания пластической деформации вводится Модель Джонсона-Кука

,                                                                  (2)

где         – предел текучести (МПа);

A – начальный предел текучести (МПа);

       – коэффициент упрочнения (МПа);

  – экспонента упрочнения (безразмерная);

 – эквивалентная пластическая деформация;

 – коэффициент скорости деформации (безразмерный);

– скорость пластической деформации (с⁻¹);

 – эталонная скорость деформации (обычно 1 с⁻¹);

 – безразмерная температура;

 – температурная экспонента (безразмерная).

При достижении критического уровня D моделируется раздробление или износ материала (рисунок 1).

Например, в модели Джонсона–Кука повреждение суммируется по уравнению инициирования повреждения:

 ,                                                                 (3)

где D₁, D₂, D₃, D₄, D₅ – экспериментальные константы материала.

σ* = σₘ / σₑᵩ*                                                                                                      (4)

коэффициент триаксиальности, представляющий отношение гидростатического напряжения к эквивалентному напряжению Мизеса.

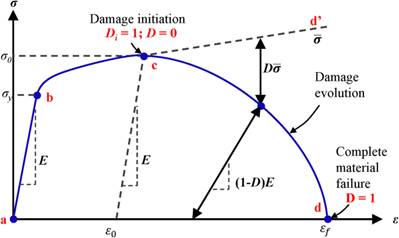
Рисунок 1. График деформации, по модели Джонсона–Кука [8]

При моделировании деталей из конструкционных сталей обычно используется Модуль Юнга. Типичное значение для углеродистых и легированных сталей E=210  ГПа. Коэффициент теплового расширения может приниматься равным α_eff=0.9, что означает – примерно 90 % пластической работы превращается в тепло (остальное рассеивается) [3].

Стандартное значение Cp для стали составляет порядка 400 Дж/(кг\К).

С помощью параметров ρ, Cp и теплопроводности k решается уравнение теплопроводности:

,                                                                                                 (5)

где  – изменение тепловой энергии в единице объема;

 – перенос тепла теплопроводностью,

Все материалы моделируются с учётом термо-механических свойств и пластичности.

Для динамических задач часто используют явные схемы (Abaqus / Explicit и др.). На основании вышеуказанных данных задаются начальные условия и ограничения, включая геометрию, зажим, скорость резания, конвективные теплоотводы и т.д.

Типовая схема этапов CAE-моделирования процесса резания показана на рисунке 2:

Рисунок 2. Схема СAE моделирования

На первом этапе исследования выбирается размерность модели (2D или 3D), задаётся геометрия инструмента и заготовки, вводятся материаловые параметры и граничные условия. После этого выполняется расчёт и последующий анализ результатов: силы резанья, температурных полей, деформаций и напряжения. Такая последовательность реализуется в большинстве систем CAE.

Сравнение методов моделирования

Ортогональное точение (2D):

Наиболее распространённый подход – двумерная постановка в плоскости, при которой игнорируется продольная геометрия инструмента. Моделируются основные зоны: зона деформации материала и зона трения «инструмент–стружка». Трение обычно описывается законом Кулона или его усовершенствованными версиями. Например, иногда применяют постоянный коэффициент скольжения, хотя более точные модели учитывают зависимость от температуры [6]. Преимущества 2D-модели: высокая скорость расчетов и приемлемая точность в оценке температурных полей и распределения напряжений в зоне резания.

Точение с вращением заготовки (3D):

Реалистичная трёхмерная модель с учётом вращательного движения заготовки и центробежных сил реализуется в Abaqus / Explicit. Модели учитывают форму спиральной стружки, кривизну фланца и вариации тепловых потоков вдоль окружности. 3D моделирование необходимо при точном прогнозе сил резки и при анализе динамики станка.

Фрезерование с отделением стружки

Фрезерование отличается прерывистым контактом зубьев инструмента с заготовкой. Модели учитывают поочерёдное вхождение и выход лезвий из резания, что вызывает дополнительные импульсы в силах и увеличивает вибрации. Важным становится моделирование обратимых нагрузок на инструмент и усталостных эффектов.

Критерии выбора модели

Выбор между 2D и 3D зависит от требуемой точности и вычислительных ресурсов. Для предварительной оценки, например, температурных полей и напряженности достаточно 2D модели (которая представлена на рисунке 3). Для точного воспроизведения эксперимента или при сложной геометрии предпочтительна 3D модель. Фрезерование всегда моделируется в 3D из-за прерывистого резания и влияния оборотов инструмента.

Результаты моделирования ортогонального точения

Силы резания (рис.3):

В симуляции определяются три основные компоненты векторов сил по осям инструмента:

Fx (главная режущая сила),

Fy (боковое сопротивление резанию),

Fz (вертикальная составляющая, связанная с силой прижатия).

Рисунок 3. Начальные геометрические условия при ортогональном точении

Численные значения сил резки вычисляются по реакциям зажимов на инструментах и анализируются в зависимости от ее режимов.

Температурные поля

Тепловые поля: моделируется уравнение теплопроводности. Это позволяет получить распределение температуры в заготовке и в инструменте. На рисунке 4 представлено температурное поле, рассчитанное для задачи ортогонального течения.

Рисунок 4. Температурное поле при ортогональном точении

Модель теплопроводности позволяет выявить зоны перегрева. На рисунке видно, что максимальные температуры наблюдаются в первичной зоне в области разделения стружки и на режущей кромке инструмента, что важно для анализа термического износа.

Практическое применение результатов

Результаты САЕ-моделирования позволяют принимать правильные инженерные решения:

Оптимизация охлаждения: по картам температурных полей можно выявлять критические зоны перегрева и направлять потоки СОЖ на наиболее горячие области.

Прогноз износа: по параметру повреждения DDD прогнозируют приближение к разрушению (например, D≈1D\approx1D≈1). Учёт модели повреждения показал увеличение прогнозируемых нагрузок; ученые [8] сообщили, что включение «damage» в модель подняло силовые прогнозы и остаточные напряжения на 10–14 %. Таким образом, при D→1D\to1D→1 можно ожидать интенсивный износ или разрушение.

Снижение вибраций: по расчёту сил резки и динамических характеристик узла вращения можно определить собственные резонансные частоты станка и режимы с минимальной вибрационной нагрузкой.

Выводы

CAE-моделирование резания показывает высокую эффективность, которая выражается в следующем:

• позволяет прогнозировать ключевые физические поля: температуру, напряжения, силы резания;
• сокращает число дорогостоящих экспериментов. Экономия по трудозатратам может достигать 40–60 %.

Особую роль играет модель Джонсона–Кука, а также учет накопления повреждений – их включение в расчёт кардинально влияет на результаты оценки износа и качества реза. Приближённые 2D-модели ортогонального точения подходят для быстрого анализа температуры и основных трендов сил. Однако для более точного анализа, особенно при учёте вращения заготовки или сложного взаимодействия инструмента с материалом, требуются 3D-модели (например, в Abaqus / Explicit). Ключевые результаты, получаемые в CAE, – это распределение температур и векторы сил резания. Их точный расчёт обеспечивает понимание физических основ процесса и позволяет оптимизировать режимы для повышения производительности и ресурса инструмента.