Оптимальные словарные раскраски взвешенных графов

Optimal word colourings of weighted graphs

Tatyana Smirnova

candidate of physical and mathematical sciences, associate professor, Lobachevsky State University of Nizhni Novgorod, Russia, Nizhni Novgorod

Аннотация. Правильная словарная раскраска графа есть сопоставление его вершинам слов, при котором слова, соответствующие смежным вершинам, находятся в отношении антипрефиксности. В статье изучаются классы графов, для которых возможно нахождение оптимальной словарной раскраски графа за полиномиальное время.

Abstract. A regular word colouring of a graph is a correspondence between words and its vertices under which the words corresponding to adjacent vertices are in the antiprefix relation. In the present article we are studуing the classes of graphs for which is possible the finding an optimal word colouring of the graph for polynomial time.

Ключевые слова: правильная словарная раскраска графа, неравенство Мак-Миллана, оптимальный префиксный код.

Keywords: regular word colouring of a graph; hydraulic systems; Macmillan’s inequality, optimal prefix coding.

В работе рассматривается задача о правильной словарной раскраске [1,2] обыкновенного графа, которая представляет собой обобщение хорошо известной задачи о правильной вершинной раскраске графа.

Правильной словарной раскраской обыкновенного графа  называется функция , где , такая, что слова, соответствующие смежным вершинам графа, находятся в отношении антипрефиксности:

,                                (1)

(здесь  − отношение антипрефиксности на паре слов, означающее, что никакое из них не является начальным отрезком другого). Две вершины графа назовем соцветными, если существует такая правильная словарная раскраска этого графа, при которой этим вершинам сопоставлены одинаковые слова.

Правильная словарная раскраска графа  может быть задана словарным вектором . Характеристикой словарной раскраски  графа  является спектральная функция словарной раскраски: , где  − длина слова , которую будем называть спектром длин словарной раскраски.

Пусть  − спектральная матрица графа , строками которой являются минимальные попарно несравнимые спектры длин словарных раскрасок графа . Отметим, что множество строк  конечно для любого графа по теореме Диксона и для любого графа может быть расшифровано, однако сложность расшифровки спектральной матрицы  может быть велика, так как задача относится к числу NP-трудных задач.

Для полных графов  правильные словарные раскраски − это в точности префиксные коды. Так как необходимое и достаточное условие существования правильной словарной раскраски  есть неравенство Мак-Миллана:

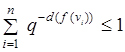,                                                   (2)

а правильная словарная раскраска на каждой клике графа  должна быть префиксным кодом, получаем очевидное необходимое условие существования правильной словарной раскраски  в виде системы неравенств Мак-Миллана:

,                                 (3)

где:  − множество всех клик графа .

При  система неравенств (3) определяет также и достаточное условие существования правильной словарной раскраски , однако при  подобное утверждение не имеет места.

Рассмотрим взвешенный граф , на вершинах которого задана вероятностная функция , где  для всех , 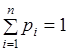. Величину  назовем стоимостью словарной раскраски  взвешенного графа .

Правильная словарная раскраска  называется оптимальной, если

.                                   (4)

Обратим внимание, что для полного взвешенного графа  оптимальная правильная словарная раскраска − есть в точности оптимальный префиксный код, который может быть получен при помощи алгоритма Хаффмана [3]. В общем случае задача оптимальной словарной раскраски взвешенного графа  включает в себя две проблемы: во-первых, построение спектральной матрицы графа , во-вторых, минимизация линейной формы относительно вероятностного вектора .

Граф G = (V, E) называется -дольным, если множество его вершин можно разбить на  непересекающихся подмножеств , , …, , так что каждое ребро графа  инцидентно вершинам из разных подмножеств  и , где . Полным -дольным графом называется -дольный граф  с разбиением вершин на доли , , …, , при котором каждая вершина любой из долей , где , соединена со всеми вершинами каждой из остальных долей.

Пусть , ,…,  ‑ разбиение вершин полного -дольного графа . В этом графе имеется в точности  клик, которые могут быть перечислены с помощью прямого произведения . Следует отметить [4], что у графов рассматриваемого класса количество клик может быть асимптотически максимальным (порядка ), поэтому сложность расшифровки спектральной матрицы для полного -дольного графа может быть весьма велика.

Рассмотрим полиномиальный алгоритм построения оптимальной правильной словарной раскраски для класса полных -дольных графов.

Пусть  ‑ взвешенный полный -дольный граф, множество вершин которого разбито на доли , ,…, , и каждой вершине  приписана вероятность .

Теорема 1. Если  − оптимальная правильная словарная раскраска взвешенного полного -дольного графа , тогда вершины, принадлежащие каждой доле графа, соцветны, т.е.  для всех .

Теорема 2. Стоимость оптимальной правильной словарной раскраски полного -дольного графа 

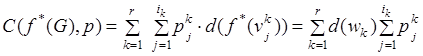,          (5)

где:  для всех .

Таким образом, для нахождения оптимальной правильной словарной раскраски взвешенного полного -дольного графа , имеет место следующий алгоритм.

Шаг 1. Определяем 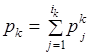 для всех . Пользуясь алгоритмом Хаффмана находим оптимальный префиксный код  относительно вероятностного вектора .

Шаг 2. Находим оптимальную правильную словарную раскраску взвешенного полного -дольного графа , учитывая соцветность вершин из каждой доли графа. Получаем  для всех .

Оценивая трудоемкость отдельных шагов алгоритма, можно установить, что она равна , где  ‑ число вершин графа.