Особенности высокоскоростного удара шара из углеродистой стали по алюминиевым и титановым пластинам

Features of high-velocity impact of a sphere of carbon steel on aluminum and titanium plates

Vladimir Meshkov

doctor of technical sciences, professor, Tver State Technical University, TvSTU., Russia, Tver

Maxim Vasiliev

сandidate of Technical Sciences, Tver State Technical University, TvSTU., Russia, Tver

Anton Kozlov

student of magistracy, Tver State Technical University, TvSTU., Russia, Tver

Аннотация. Оценка высокоскоростных воздействий на элементы конструкций является важной задачей при проектировании современной техники. В работе проведено компьютерное моделирование высокоскоростного удара шара по пластинам, дана оценка защитных свойств исследуемых пластин, а также определена минимальная толщина пластин, при которой шар не пробивает конструкцию.

Abstract. Assessment of high-velocity impacts on structural elements is an important task in the design of modern engineering. In work, a computer simulation of a high-speed velocity of a sphere on obstacles has been carried out, an assessment of protective properties of investigated plates is given, in which the sphere does not break through the structure.

Ключевые слова: высокоскоростной удар; напряжённо-деформированное состояние; компьютерное моделирование; пластины; метод конечных элементов.

Keywords: high-velocity impact; stress-strain state; computer simulation; plates; finite element method.

1.  Актуальность исследования

В процессе проектирования новых изделий в различных отраслях машиностроения требуется учёт возможных процессов, связанных с интенсивными высокоскоростными воздействиями различной природы, сопровождающиеся большими деформациями и разрушением элементов конструкций. Оценка и анализ напряжённо-деформированного состояния твёрдых тел при высокоскоростном ударе представляет собой важное направление в обеспечении безопасности и нормального функционирования изделий.

Существует два основных метода решения рассматриваемых задач: проведение экспериментальных исследований и компьютерное моделирование. Экспериментальные исследования обладают высокой точностью и достоверностью, но стоимость проведения эксперимента высока и занимает длительное время. Наиболее перспективным является компьютерное моделирование в специализированных программно-вычислительных комплексах конечно-элементного моделирования (ANSYS, ABAQUS и др.). Компьютерное моделирование позволяет получать нужную информацию в интересующей точке взаимодействия твёрдых тел, даёт возможность оценивать степень деформации и разрушения исследуемых объектов. Этот метод получил широкое распространение и применяется как в отечественных, так и зарубежных исследованиях.

В исследовании [3] моделировался процесс группового удара высокоскоростных элементов по космическому аппарату. Авторы отмечают, что применение численных методов представляется теоретически и практически важной задачей. Результаты моделирования показали, что воздействие высокоскоростных элементов группы стержней представляет большую опасность по сравнению с воздействием одиночного ударника. В работе разработана численная методика, позволяющая моделировать процессы взаимодействия оболочек космических аппаратов с высокоскоростными стержнями в широком диапазоне скоростей.

В работе [4] проведено расчётно-экспериментальное исследование стойкости брони при воздействии пули калибра 7,62 мм. Результаты компьютерного моделирования показали хорошее соответствие с экспериментальными данными. На основе результатов расчёта была выбрана наиболее рациональная конфигурация брони и разработана конструкторская документация противоосколочной защиты кузова-контейнера.

В работе [6] представлено экспериментальное и численное исследование поведения многослойных композитов. Натурные испытания на пробитие были проведены на многослойных панелях, наружный слой которых состоял из алюминиевого сплава или титанового сплава, а внутренний наполнитель из композита на основе полиэфирэфиркетона (ПЭЭК). Результаты моделирования находятся в хорошем согласовании с экспериментальными данными, максимальная ошибка с результатами эксперимента составила 15%. Авторы отмечают, что многослойные композиты на основе ПЭЭК являются перспективным материалом для применения в противоударных элементах различных конструкций.

Целью настоящей работы является оценка высокоскоростного воздействия стального ударника на алюминиевые и титановые пластины, а также подбор оптимальной конструкции препятствующей пробитию.

2.  Постановка задачи

Расчётная схема представляет собой две плоские прямоугольные пластины размером 76х76 мм. Пластины закреплены жёсткой заделкой за боковые грани. Ударяющее тело – шар диаметром 7,6 мм из стали У12А. Скорость шара составляет V = 800 м/с, вектор скорости направлен перпендикулярно к поверхности пластины в её центр. В работе рассматривается удар по двум разнесённым на расстояние 15 мм пластинам трёх конструкций:

A.материал 1 и 2 пластины – алюминиевый сплав АМг6, толщина 1 пластины h = 3 мм, толщина 2 пластины h = 2 мм;

B. материал и толщина 1 пластины аналогичны конструкции А, материал 2 пластины – титановый сплав ВТ6 толщиной h = 2 мм;

C. материал и толщина 1 пластины аналогичны конструкции А, материал 2 пластины – титановый сплав ВТ6 толщиной h = 3 мм.

В таблице представлены свойства используемых материалов, приведённые из [1; 2; 5].

Таблица 1.

Свойства материалов

3.  Компьютерное моделирование

Компьютерное моделирование проводится методом конечных элементов в программном комплексе ANSYS/LS–DYNA.

В программном комплексе для расчёта применяется пластическая кинематическая модель материала (Plastic Kinematic), использующая определяющее уравнение Купера-Саймондса (Cowper-Symonds):

                                 ,                                       

где: 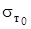 – статический предел текучести, МПа;  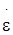– скорость деформации, с^-1; D, P – коэффициенты уравнения;  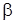– параметр упрочнения; 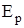– модуль упрочнения, МПа;  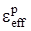– эффективная пластическая деформация.

Используемая модель учитывает кинематическое и изотропное упрочнение, а также описывает зависимость динамического предела текучести 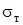 от скорости деформации. Критерием разрушения является достижение эффективной пластической деформацией  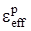предельного значения.

При построении сетки конечных элементов используется элемент 3D Solid 164, представляющий собой объёмный шестигранник с восьмью узлами, расположенными в вершинах. Сетка конечных элементов пластин имеет сгущение в месте взаимодействия тел. Средний размер конечных элементов шара и пластин равен 0,9 мм.

Количество слоёв конечных элементов составляет 3 слоя при толщине пластины h = 2 мм, и 4 слоя при толщине пластины h = 3 мм.

Для моделирования контактного взаимодействия в расчёте используется эрозионный тип контакта. Выбранный тип характеризуется тем, что контакт между телами происходит по поверхностям. Если поверхность, состоящая из узлов, разрушилась, в контакт вступают следующие узлы.

4.  Результаты моделирования

Результаты моделирования высокоскоростного удара шара по трём различным конструкциям показали следующее.

Конструкция А.

Стальной шар пробил насквозь две алюминиевые пластины, рисунок 1а. На периферии сквозных отверстий образовались две лунки. Максимальные перемещения в 1 пластине равны l_max ≈ 2,4 мм, а во 2 пластине – l_max ≈
≈ 3,5 мм. Диаметр отверстия в 1 пластине равен d₁ ≈ 8,19 мм, во 2 равен d₂ ≈
≈ 8,2 мм. Скорость шара после пробития 1 пластины упала на 120 м/с, что составляет 15 % от начальной скорости шара. После пробития 2 пластины скорость шара упала на 75 м/с, что составляет 9,4 % от начальной скорости. Масса шара после пробития пластин практически не изменилась, образовалась пластическая деформация в виде вмятины.

Конструкция Б.

В алюминиевой и титановой пластинах шар пробил сквозное отверстие, рисунок 1б. На периферии сквозных отверстий также образовались две лунки. Скорость шара, диаметр отверстия и максимальные перемещения после пробития алюминиевой пластины аналогичны ранее зарегистрированным показателям в первой конструкции. Максимальные перемещения во 2 пластине равны l_max ≈ 8 мм. Диаметр отверстия во 2 пластине равен d₂ ≈ 7,8 мм. После пробития титановой пластины скорость шара упала на 280 м/с, что составляет 35 % от начальной скорости. В результаты пробития двух пластин произошло местное разрушение шара. Масса ударяющего тела уменьшилась на 0,19 г, что составляет 10,5 % от начальной массы, рисунок 2а.

Конструкция В.

Шар насквозь пробил алюминиевую пластину, а в титановой пластине оставил вмятину, рисунок 1в. Скорость шара, диаметр отверстия и максимальные перемещения после пробития алюминиевой пластины аналогичны ранее зарегистрированным показателям в первой конструкции.

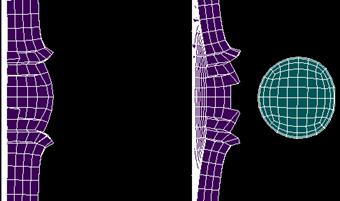
а)                                  б)

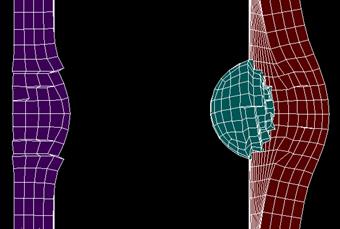
в)

Рисунок 1. Деформированная модель: а – конструкция А; б – конструкция Б; в – конструкция В

Максимальные перемещения во 2 пластине равны l_max ≈ 5,8 мм. Максимальные напряжения в области контакта 2 пластины и шара составляют σ_max ≈ 1250 МПа, что превышает предел прочности σ_в титанового сплава. При данных напряжениях происходит локальное разрушение нескольких слоёв конечных элементов титановой пластины, и, вероятно, образуются трещины рядом с областью удара.

После контакта со 2 пластиной и ее прогиба, скорость шара упала, после чего траектория движения шара изменилась на противоположную по оси удара, а его скорость составила 40 м/с. В результате контакта с титановой пластиной масса шара упала на 0,642 г, что составляет 35,7 % от начальной массы, рисунок 2б.

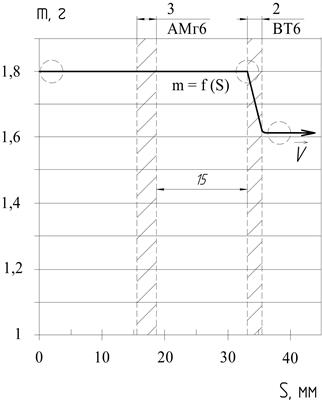
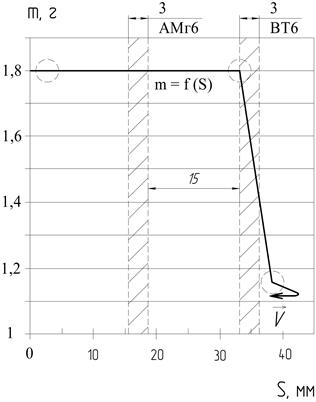
а)                                  б)

Рисунок 2. График зависимости массы шара от пройденного пути S: а – конструкция Б; б – конструкция В

Оптимальной конструкцией препятствующей пробитию, является конструкция В: первая пластина – АМг6 толщиной h = 3 мм, вторая пластина – ВТ6 толщиной h = 3 мм.