Напряженно-деформированное состояние металл-полимерных трубопроводов

The title of scientific paper

Vladimir Oparin

Doctor of Science, associate Professor, Samara state University, Russia, Samara

Aleksandr Sinygin

graduate student Samara state University, Russia, Samara

Аннотация. Изучение напряженно-деформированного состояния армированных труб. Получена расчетная эквивалентная модель для такого типа труб. Разработанные принципы могут быть использованы на этапах конструирования, проектирования и эксплуатации армированных труб.

Abstract. Study of stress-strain State of metal-polymer pipelines. Analytical and experimental method. Received an estimated equivalent design model for reinforced pipes. Principles developed can be used on stages of construction, design and operation of reinforced metal pipes.

Ключевые слова: напряженно-деформированное состояние; анали­тический и экспериментальный метод, проектирование и эксплуатация армированных труб.

Keywords: stress-strain State; analytical and experimental method, design and operation of reinforced pipes.

Острой проблемой нефтегазодобывающей отрасли являются аварии промысловых трубопроводов. В настоящее время на нефтепромыслах страны действует разветвленная система нефтепроводов, продуктопро­водов общей протяженностью более 300 тыс. км.

Ежегодно происходит около 50-70 тыс. нарушений герметичности и разрывов труб. При этом количество аварий с каждым годом возрастает в связи с износом металлических трубопроводов и увеличением их протяженности.

Основной причиной аварий является коррозия металла. Из общего числа аварий до 55 % приходится на долю систем нефтесбора и 30-35 % – на долю линий поддержания пластового давления (ППД). При этом 42 % труб не выдерживают пятилетней эксплуатации, а 17 % – и двух лет.

Альтернативой металлическим трубопроводам являются коррозионно-устойчивые армированные трубопроводы, которые обладают рядом преимуществ перед традиционными стальными трубопроводами. Они имеют высокую коррозионную стойкость; возмож­ностью монтажа секциями до 250 м; наличием разъемных соединений. Это позволяет при монтаже отказаться от проведения сварочных работ. Такие трубы обладают высокой технологичностью монтажа; а также низкой степенью шероховатости поверхности, что уменьшает гидравлическое сопротивление в трубопроводной системе.

Предметом исследования в настоящей работе являются гибкие полимерно-металлические трубы (ГПМТ) со стальным проволочным каркасом.

Ранее расчетные модели для такого типа труб строились на методике расчета шлангокабелей, что не совсем является корректным. Более точные модели практически не поддаются расчетам, поскольку неизвестны многие коэффициенты взаимодействия различных слоев, из которых состоит труба.

В данной работе представлена эквивалентная модель, описывающая многослойную гибкую трубу как двухслойный сплошной тонкостенный цилиндр с ортотропными механическими свойствами каждого из слоев. Сформулирован метод заполненного периметра, использованный для расчета механических свойств эквивалентной двухслойной модели, а также дан сравнительный анализ результатов расчета модели и традиционных расчетных методик.

Рисунок 1. Гибкая армированная труба

Примечание: 1 – внутренняя камера из полиэтилена низкого давления (ПНД); 2 – стальной проволочный каркас; 3 – гидроизолирующие из клейкой поливинилхлоридной ленты (ПВХ); 4 – грузонесущие повивы из полипропиле­нового шпагата (ПП); 5 – внешний слой из экструдированного полиэтилена высокого давления (ПВД).

В ходе исследования гибких труб выдвинуто предположение о возможности замены многослойной конструкции гибкой трубы экви­валентной двухслойной моделью с такими механическими свойствами, чтобы внутренний слой воспринимал радиальные нагрузки, а внешний – осевые, причем передача осевой составляющей внутреннего давления происходила от внутреннего слоя к внешнему.

Минимально допустимый радиус изгиба ГПМТ составляет 0,6; 0,75 и 1,1 метра в зависимости от условного диаметра. В местах изгиба будет наблюдаться увеличение шага спирали по внешней образующей дуги трубы и, как следствие, местное уменьшение прочности конструк­ции. В этом случае требуется определить значения безразмерных коэффициентов a и b для внутреннего и внешнего слоя модели. Площадь соприкосновения внутренней трубы с металлическим бандажом при ее изгибе несколько увеличивается, и новое значение коэффициента a₁ (см. ниже) составит 0,71 в отличие от 1 (для недефор­мированной трубы).

Для определения значения Е_{радиальное} в программном комплексе ANSYS были построены 6 пар моделей с внутренними диаметрами 69, 85, 96, 105, 116 и 125 мм. Толщина проволоки спирального проволочного бандажа и цилиндрической стенки во всех случаях составила 3 мм, шаг спирали – 3,2 мм. Все модели были нагружены внутренним давлением в 5 МПа.

Результаты моделирования представлены в Таблице.

Таблица 1.

Деформация спиральных и цилиндрических моделей

Отношение деформации цилиндров к деформации спиралей будет определяться коэффициентом а₂, характеризующим величину Е_{радиальное}:

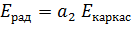
Таким образом, для рабочих параметров необходимо соблюдение следующих условий.

1.    для внутреннего слоя модели:

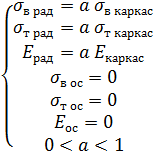                                                                                                           (1)

где:   σ_{в рад}, σ_{т рад}, Е_рад – пределы прочности, текучести и модуль Юнга внутреннего слоя эквивалентной модели в радиальном направлении; σ_{в ос}, σ_{т ос}, Е_ос – в осевом; σ_{в каркаса}, σ_{т каркаса}, Е_{каркаса} – механические свойства воспринимающего радиальные нагрузки материала прово­лочного каркаса;

2.    для внешнего слоя модели:

                                                                                                             (2)

где:   σ’_{в ос}, σ’_{т ос}, Е’_ос – пределы прочности, текучести и модуль Юнга внешнего слоя эквивалентной модели в осевом направлении; σ’_{в рад}, σ’_{т рад}, Е’_рад – в радиальном; σ_{в груз}, σ_{т груз}, Е_груз – механические свойства материалов, воспринимающих осевые нагрузки.

Геометрические размеры слоев эквивалентной модели совпадают с размерами основных грузонесущих слоев гибкой трубы. Внутренний слой имеет толщину 3 мм, что соответствует толщине слоя проволочного каркаса, а внешний – 8 мм, что равно толщине слоя грузонесущих повивов. (см. рис. 1).

В качестве вывода можно заключить, что впервые представлена эквивалентная двухслойная цилиндрическая модель, заменяющая при прочностном расчете многослойную модель композитной армированной трубы. Получены и обоснованы ортотропные значения механических свойств слоев эквивалентной модели. Определено влияние на осевую прочность конструкции всех слоев армированной трубы.