Определение оптимальных размеров пластиковой катушки для сварочной проволоки

Definition the optimal size of the plastic spool for welding wire

Sergey Konev

candidate of engineering sciences, assistant professor of Magnitogorsk state technical University named after G.I. Nosov, MGTU, Russia, Magnitogorsk

Vladimir Mikhaylets

candidate of engineering sciences, assistant professor in Magnitogorsk state technical University named after G.I. Nosov, MGTU, Russia, Magnitogorsk

Ivan Teftelev

head of preproduction Department in Magnitogorsk hardware-metallurgical plant- United joint stock company - OAO “MMK-Metiz”, Russia, Magnitogorsk

Аннотация. В промышленности нашли широкое применение пластиковые катушки для смотки металлической проволоки и полимеров. Однако имеет место разрушение катушек. В статье исследуются напряжения и упругие деформации в наиболее нагруженных точках катушки. По результатам расчетов выбраны оптимальные соотношения размеров бокового элемента катушки.

Abstract. In industry widely used plastic spool for coiling metal wire and polymers. However, there is a breakage of the spool. The article examines the tensions and elastic deformations in the most loaded points of the spool. According to the analysis selected the optimal ratio of the size of the spool`s sidewall.

Ключевые слова: пластиковая катушка; элементы катушки; гибкая круглая пластина; напряжения; упругие деформации.

Keywords: plastic spool; details of spool; flexible round plate; tensions; elastic deformations.

Пластиковые катушки типоразмеров Д200 и Д300 по ГОСТ 25445-82 широко используются в промышленности, в частности, для смотки проволоки, полимерного кабеля для 3D-принтеров и т.д. Конструктивно катушка состоит из двух плоских боковин 1 (рис. 1), имеющих форму кольцевой пластины, и жестко соединяющих их барабана 2.

При использовании пластиковых катушек для смотки сварочной проволоки на ОАО «ММК-МЕТИЗ» отбраковывается до 10% катушек по причине разрушения боковины катушки (сколы боковины и ее отрыв от барабана с образованием трещины 4 на начальной стадии отделения). Разрушения катушек происходят при многорядной намотке проволоки на барабан, как следствие упругой деформации от давления витков проволоки на боковины. Определение причин разрушения катушек особенно актуально при использовании для изготовления катушек пластиковых материалов вторичной переработки, которые обладают худшими прочностными характеристиками. Поэтому необходимо исследовать напряженно-деформированное состояние боковины катушки и определить места опасных напряжений.

Боковина катушки 1 представляет пластину с круговым вырезом, жестко защемленную в сердечнике 2 катушки, нагруженную перпендикулярно ее срединной плоскости распределенной нагрузкой. В результате действия нагрузки образуется трещина 4.

Рисунок 1. Схема конструкции пластиковой катушки и нагрузки на боковину

Для выяснения причин разрушения катушки рассмотрим её боковину, как тонкую упруго деформируемую пластину, имеющую форму кольца с размерами b, a и h, где b - внешний радиус, а – внутренний радиус, h – толщина боковины (рис.2, h/ b ≪1). Исследуемая пластина жестко закреплена по внутренней окружности радиуса а. Нагрузку q в первом приближении будем считать равномерно распределенной по высоте смотки, т.е. q = const.

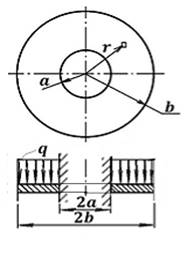
Рисунок 2. Расчётная схема нагружения боковины катушки

Проведенными испытаниями в сталепроволочном цехе ОАО «ММК-Метиз» установлено, что реальные прогибы боковины не превышают ее толщины (см. таблицу). Методика испытаний заключалась в замере расстояния между боковинами катушки после ее полного заполнения (до диаметра 2b) по стандартной технологии намотки проволоки на линии рядной намотки проволоки.

Таблица

Упругие деформации боковины катушки

Таким образом, для расчета напряженно-деформированного состояния точек боковины катушки можно применить уравнения теории упругости для тонких гибких пластин [1]:

Для решения воспользуемся дифференциальными уравнениями Софи Жермен [2]:

                                                                      (1)

где

w – поперечная деформация пластины;

q – поперечная нагрузка на боковину;

r –радиус положения точки;

D – цилиндрическая жёсткость пластины,

Выделяя кольцевую часть пластины от радиуса a до радиуса r (r – текущая координата внутри интервала (a, b), рис. 3), найдем Q(r) – уравновешивающую поперечную силу, возникающую в пластине и необходимую для составления частного и общего решений уравнения (1).

Рисунок 3. Схема для определения равновесного состояния пластины

Поскольку из уравнения равновесия части пластины    следует, что

                                                                             (2)

то получаем необходимое для решения выражение поперечной силы

                                                                                             (3)

Тогда частное решение уравнения (1) может быть найдено в виде:

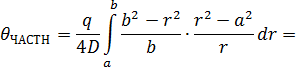
                                                                      (4)

А общее решение уравнения (1) будет иметь вид:

                                                                   (5)

Подставляя в решение граничные условия  при  и  при  , получим уравнения для нахожденияпостоянных интегрирования A и B.

Определим выражения изгибающих моментов действующих на боковину вдоль радиуса r и в ортогональном ему направлении.

                                                         
     и 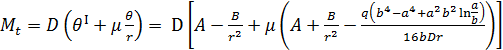                                                         (6)

Для оценки прочности пластинки необходимо найти напряжения, которые будут максимальны при  и находиться на поверхности пластинки при :

                                                                                    (7)

Поскольку материал пластинки пластичный (ударопрочный полистирол), то оценим его эквивалентные напряжения по третьей теории прочности:

                                                                (8)

Из анализа выражения (8) видно, что эквивалентные напряжения обратно пропорциональны радиусу положения точки r и поэтому максимальное значение они будут иметь при r = a.

Найденные из выражения (8) величины напряжений в критических точках исследуемой боковины катушки, при отношении диаметров  a/b = 0,3…0,9, (при заданных значениях q, h, b и при использовании полимерных материалов с различным коэффициентом Пуассона [3], представлены на графике на рис. 4. Анализ графика позволяет утверждать, что при прочих равных параметрах, оптимальный размер внутреннего (посадочного) диаметра катушки должен составлять не менее 0,5 внешнего диаметра этой катушки.

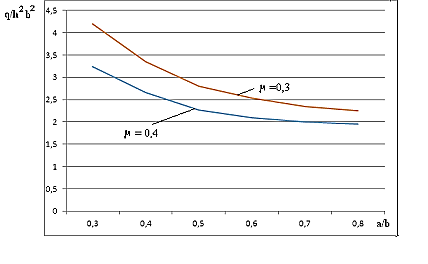
Рисунок 4. Зависимость напряжений в боковине катушки от параметра a/b

Выводы:

- Определены напряжения в материале бокового элемента катушки для намотки проволоки, как пластины с круговым вырезом, нагруженной распределенной нагрузкой постоянной интенсивности в радиальном направлении, с использованием разрешающего уравнения С. Жермен.

- С использованием полученных разрешающих уравнений установлены оптимальные соотношения размеров бокового элемента пластиковой катушки.