Сверхбыстрое нахождение всех простых чисел – формула
Конференция: VII Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Секция: Математическая логика, алгебра и теория чисел

VII Международная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Сверхбыстрое нахождение всех простых чисел – формула
ULTRA FAST FINDING ALL THE PRIME NUMBERS: FORMULA
Viktor Shcherban
student, faculty of mathematics and information technology, Kurgan State University, Russia, Kurgan
Аннотация. Нахождение очень больших простых чисел до сих пор считается трудоемкой работой. Существующие алгоритмы уже используют разложение на простые множители чисел, которые превышают 10110. Это целые сутки непрерывной работы самого мощного в мире ЭВМ. Теперь мы убедимся в обратном – никаких алгоритмов простоты произвольного числа не требуется. Достаточно выбрать конкретный порядковый номер числа Фибоначчи и произвести несложные арифметические действия. Для очень больших чисел Фибоначчи, это непродолжительная работа среднемощного компьютера и результат готов. Огромные простые числа лежат в основе защиты электронной коммерции и электронной почты. Поскольку некоторым злоумышленникам со временем все же удается их вычислить, то знающие шифровальщики постоянно обновляют арсенал огромных простых чисел – это практика, а простая любознательность и научный престиж будет стимулировать охотников за большими простыми числами, так это теория.
Abstract. Finding very large prime numbers is still considered a hard work. Existing algorithms already employ splitting numbers into simple multipliers, which exceed 10110. This well takes 24 hours of the world’s most powerful ECM. Now we shall prove the opposite: no algorithms of random number primality is needed. Not a continuous work of a medium-power computer and the result is ready. The large prime numbers make the basis for protection of electronic commerce and electronic post. As some of intruders gradually manage to compute them, knowing cryptologists keep renewing inventory of the large prime numbers, which is a practice, while a mere curiosity and a scientific prestige will stimulate hunters for the large prime numbers, which is a theory.
Ключевые слова: простые числа; числа Фибоначчи; арифметические числовые таблицы.
Keywords: prime numbers; Fibonacci sequence; arithmetic number table.
До сих пор предмет арифметики, как науки о целых числах, не смог даже точно составить вопрос (именно так), об обобщении всех арифметических числовых таблиц и бесспорно определить те правила вещественных действий, которые для таблиц должны иметь место. Арифметические таблицы в отличие от всех других таблиц можно расположить в трёхмерном пространстве, где обозначение цифровых символов, например, можно заменить количеством натуральных (вещественных) предметов. Современные арифметические числовые таблицы умножения - это просто элементарные таблицы для быстрого счета. Одновременно они же являются для не направленного нахождения всех составных чисел в ряде натуральных чисел. В нашей квалификации они являются числовыми таблицами Первого Порядка.
Математическая логика подсказывала, что должны существовать таблицы для не направленного, а возможно и направленного, нахождения всех простых чисел. Это логическое изыскание привело к открытию числовых таблиц Второго Порядка (рекуррентных последовательностей) и нахождению простых чисел с помощью возвратных рядов, например, чисел Фибоначчи (см. таблица 1). И что самое главное, так это для правильного понимания ниже предоставленного уникального математического материала, нет нужды в предварительных знаниях, кроме умения производить несложные тождественные преобразования.
Теперь приступаем к непосредственному нахождению простых чисел – всех или конкретных. Для этого предоставим уникальное решение главной задачи всей арифметики, которое было приведено в авторской работе, но без полного и исчерпывающего доказательства [1]. Рассмотрим самый известный ряд чисел Фибоначчи, у которого каждое порядковое число равно сумме двух предыдущих чисел, а первые два числа равны нулю и единице. Первые двадцать одно число этой возвратной последовательности, следующие:
Vq = 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765…
Числовое сравнение: Vq + Vq+2 ≡ 1(mod q),
разрешимо только тогда, когда порядковый номер (q) – есть число простое!
Порядковый номер – это позиционное место конкретного числа Фибоначчи во всем его числовом ряду. Примеры:
семнадцатое число этого ряда равно 987, девятнадцатое число равно 2584,
значит: V17 + V19 – 1 = 987 + 2584 – 1 ≡ 0(mod 17),
далее: V18 + V20 – 1 = 1597 + 4181 – 1 ≢ 0(mod 18),
девятнадцатое число равно 2584, двадцать первое число равно 6765,
значит: V19 + V21 – 1 = 2584 + 6765 – 1 ≡ 0(mod 19);
Доказательством данного утверждения есть составленная беспредельная арифметическая таблица (см. таблицу 1).
Для больших чисел Фибоначчи воспользуемся услугами интернета и еще раз убедимся, что определение простоты любого наперед заданного числа есть невероятно простая задача [2].
В представленной таблице – первое число не натуральное и равно нулю (очень важное уточнение, так как нуль не является натуральным числом).
Например, выберем простое число 53.
Пятьдесят третье число Фибоначчи равно: 32 951 280 099.
Пятьдесят пятое число Фибоначчи равно: 86 267 571 272.
Значит: (32951280099 + 86267571272) – 1 = 53(2249412290) ≡ 0(mod 53).
Следующее простое число 59.
Пятьдесят девятое число Фибоначчи равно: 591 286 729 879.
Шестьдесят первое число Фибоначчи равно: 1 548 008 755 920.
Значит: (591286729879 + 1548008755920) – 1 = 59(36259245522) ≡ 0(mod 59).
Для ясности – выше приведенное арифметическое положение можно перевести и в элементарную алгебраическую форму.
Повторим и рассмотрим самый известный числовой ряд Фибоначчи (Vq), у которого первые два числа являются нуль и единица.
Система числовых сравнений разрешима только тогда,
когда порядковый номер (q) – [mod q], есть число простое:
{ 5-е число Фибоначчи } + { 7-е число Фибоначчи } – 1 ≡ { результат: (mod 5) },
{ 6-е число Фибоначчи } + { 8-е число Фибоначчи } – 1 ≡ { результат: (mod 6) },
{ 7-е число Фибоначчи } + { 9-е число Фибоначчи } – 1 ≡ { результат: (mod 7) },
Vq + Vq+2 – 1 ≡ 0(mod q), (1)
в точности: левая сторона данной формулы является формой количественной, а правая сторона – качественной и является поместным (позиционным) порядком каждого конкретного числа Фибоначчи. Например, если первое число ряда Фибоначчи взять натуральное число один, тогда формула (1) будет иметь другой вид.
Подтверждаем, что нахождение простых чисел не требует особых знаний, а только умение производить не сложные арифметические действия.
Следующее простое число 61.
Шестьдесят первое число Фибоначчи равно: 1 548 008 755 920.
Шестьдесят третье число Фибоначчи равно: 4 052 739 537 881.
Значит: (1548008755920 + 4052739537881) – 1 = 61(91815545800) ≡ 0(mod 61).
Множество числовых рядов с нахождением простых чисел бессчетно (то есть, невозможно подсчитать), так как они взяты, включая числа Фибоначчи, из арифметического треугольника Паскаля, который бесконечен [3]. Данное утверждение не приводится, в виду числовой громоздкости его изложения, но принцип нахождения и построения некоторых числовых рядов необходимо объяснить. Например, к возвратному уравнению ряда Фибоначчи прибавим число один. Тогда получим новый числовой ряд, у которого каждое число равно сумме двух предыдущих чисел с прибавлением единицы: W1 = 0, W2 = 1, W3 = 2, W4 = 4, W5 = 7,...; (см. таблицу 1).
Первые пятнадцать чисел этого ряда в математическом виде:
(Wq) = 0,1,2,4,7,12,20,33,54,88,143,232,376,609,986,…; (Wq = Wq-1 + Wq-2 + 1).
Отметим только одно из всего множества числовых свойств данного ряда чисел.
Числовое сравнение: 2(Wq) – Wq-1 ≡ 0(mod q), разрешимо только тогда, когда порядковый номер (q) – есть число простое. Примеры:
2(W11) – W10 ≡ 0(mod 11), или , 2(143) – 88 = 11·18 ;...,
2(W13) – W12 ≡ 0(mod 13), или , 2(376) – 232 = 13·40 ;...;
Над натуральными числами существуют только три равновеликих по сути безграничных и беспредельных арифметических действий, которые можно отобразить в виде бесконечных арифметических таблиц.
1. Числовые таблицы операций сложений: их последовательная сумма есть действие сложение.
2. Числовые таблицы операций умножений или таблицы для быстрого счета: их последовательная числовая сумма есть действие умножение. Они же служат для не направленного нахождения всех составных чисел. Эти таблицы нам известны с первого класса начальной школы.
3. Числовые таблицы операций сравнений (общепринятое понятие – по числовому модулю) или таблицы для сверхбыстрого и мгновенного счета: их не последовательная числовая сумма есть действие сравнение. Они же служат для направленного нахождения всех простых чисел.
Сверхбыстрый простой пример: число сто сравнимо с числом три или нет? Сложный, но тоже быстрый по результату пример: сравнимость простых чисел в числовых последовательностях (1). Первая из множества таких таблиц рассмотрена – далее, (см. таблицу 1).
В арифметике как науке, математическое действие деление натуральных чисел на чисел отсутствует, потому что фактически оно не определено. Так как в числовых таблицах отсутствует операция деления, тогда сравнимость чисел (ɑ) и (b) по модулю (q), означает только возможность представить (ɑ) в виде (ɑ = b + qt ), где число (t) – целое.
Уникальные по значимости и объёму таблицы по числовому модулю, начиная с ряда Фибоначчи, найдены из треугольника Паскаля, построенного в трёхмерном пространстве, где значение чисел можно заменить реальными натуральными предметами. Все выше названные числовые таблицы имеются у автора данной публикации.

Рассмотрим общий принцип составления арифметических таблиц и как ими пользоваться. Начнем с самой известной возвратной последовательности чисел – ряда Фибоначчи. Каждое число Фибоначчи (Vq ) равно сумме двух предыдущих чисел: 0,1,1,2,3,5,8,13,21,34,55,89,…(Vq = Vq–1 + Vq–2 ).
Следующий второй (Wq ) возвратный числовой ряд: 0,1,2,4,7,12,20,33,54,88,… имеет возвратное уравнение с прибавлением единицы - (Wq = Wq–1 + Wq–2 + 1).
Теперь составим следующую общую числовую таблицу Второго Порядка для нахождения всех простых чисел. Основное числовое свойство таблицы размещается посредством действий (операций) над числами, лежащими на фиксированных горизонталях.
Таблица 1.
Нахождение всех простых чисел
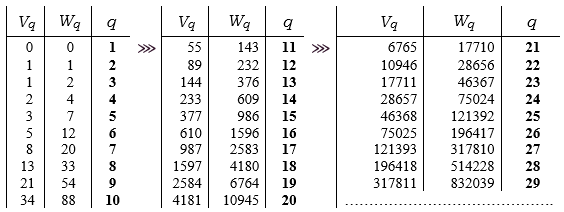
Числовое сравнение: Vq + Wq ≡ 0(mod q), разрешимо только тогда, когда порядковый номер (q), есть число простое. Примеры:
V17 + W17 = 987 + 2583 ≡ 0(mod 17),
V18 + W18 = 1597 + 4180 ≢ 0(mod 18),
V19 + W19 = 2584 + 6764 ≡ 0(mod 19)…;
Для нахождения формулы имеем очевидное числовое равенство: Vq = Wq–2 + 1.
И тогда: Vq + Vq+2 ≡ 1(mod q), что соответствует ряду чисел Фибоначчи (1).
Числовые таблицы сравнений по реальному модулю являются таблицам Второго Порядка (сумма существующих арифметических операций таблиц Первого Порядка). В основе любой отдельно взятой числовой таблицы должен лежать первородный возвратный ряд чисел – любые два соседних числа такой последовательности равны нулю и единице. Первородный ряд чисел имеет возвратное уравнение: (Vq = Vq–k + Vq–s). Количество классов определяется числом (k). Каждый класс имеет свою группу подклассов (s).
Осталось особо отметить, что не все числовые свойства возвратных рядов могут быть закодированы, а значит, найдены в арифметическом пространстве для натуральных чисел, это например, следующий числовой ряд:
(Vn) = 7,7,31,79,151,247,…(Vn = 3Vn–1 – 3Vn–2 + Vn–3).
Данная числовая возвратная последовательность имеет исключительное числовое свойство. Все простые сомножители каждого порядкового члена, имеют только вид:
(p – 1) ≡ 0(mod 3), например, (V6 = 247 = 13 ·19), (V16 = 2527 = 7 · 19 · 19).
Современные арифметические числовые таблицы сложения реально и разумно изъяты из безусловного закона Паскаля – «возмущения», действующего в одноименной арифметической таблице – треугольника, но само понятие сложение так формально и не определено. Теперь будет ясно почему. Действующие числовые таблицы сложения, а далее таблицы для быстрого счета (умножения), лишены беспредельной числовой памяти – первородных возвратных рядов, поэтому для умноженных чисел, это таблицы Второго Порядка, действие (не операция!) сложения НЕ равносильна умножению.


