Структурный и кинематический анализ кривошипно-ползунного механизма

STRUCTURAL AND KINEMATICAL ANALYSIS KROVOSHIPNO-SOLUBLE MECHANISM

Oleg Pavlov

associate professor of the Leninogorsk Branch of the FGBOU IN THE KNITU them A.N. Tupolev – KAI, Russia, the Republic of Tatarstan, Bugulma

Аннотация. Статья посвящена методике проведения практических занятий по анализу механизмов различного типа со студентами машиностроительного профиля. Рассмотрен пример проведения структурного и кинематического анализа кривошипно-ползунного механизма с подробным описанием методики выполнения домашних заданий по учебной дисциплине «Теория механизмов и машин». Методика предполагает повышение практических навыков обучающихся, прежде всего за счет индивидуализации обучения.

Ключевые слова: механизм; структура; кинематика; анализ; звено; пара; цепь; скорость; ускорение.

Кинематическую основу любой машины составляют механизмы, предназначенные для преобразования заданного движения входному (ведущему) звену в требуемые движения остальных звеньев, как правило, с изменением скоростей и ускорений [1].

Одной из основных задач учебной дисциплины «Теория механизмов и машин» является производство структурного и кинематического анализа механизмов. В процессе обучения студентов качественному выполнению данной процедуры приходится сталкиваться с недостаточным количеством учебного времени, особенно при заочном и очно-заочном обучении. Для  повышения эффективности получения студентами практических навыков анализа работы различных типов механизмов предлагается выдавать им в качестве домашних индивидуальных заданий выполнение структурного и кинематического анализа механизма по схеме, предложенной ниже для кривошипно-ползунного механизма с учетом рекомендаций авторов [1].

Структурный анализ механизма. Структурная схема, исходные данные и общий анализ механизма.

Исходные данные:

- начальное положение ведущего звена кривошипа φ₁ = 45°;

- размеры звеньев: ℓ_ОА = 0,05 м; ℓ_АВ = 0,20 м.

- частота вращения ведущего звена n = 765 об/мин.

Структурная схема механизма представлена на рисунке 1. На ней указаны неподвижное звено (стойка), подвижные звенья, заглавными латинскими буквами обозначены центры вращения кинематических пар, входное звено и направление его движения. Звенья на схеме обозначим арабскими цифрами 1, 2, 3, 4, начиная с входного (ведущего) звена.

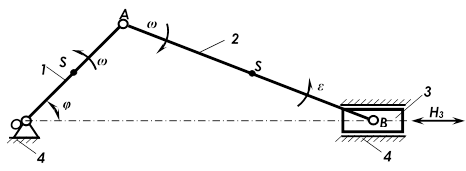
Рисунок 1. Схема кривошипно-ползунного механизма

Определение числа звеньев, кинематических пар  и их характеристика

Данный механизм включает четыре звена [2].

Звено 1 – кривошип, который совершает полнооборотное вращательное движение.

Звено 2 – шатун-звено, совершающее сложное плоскопараллельное движение и образующие кинематические пары только с подвижными звеньями.

Звено 3 – ползун, совершает возвратно-поступательное движение.

Звено 4 – стойка, неподвижна.

Число подвижных звеньев n = 3.

Кинематические пары (КП), образуемые звеньями [2]:

4 - 1 ("0") – вращательная, одноподвижная, низшая;

1 - 2 ("А") – вращательная, одноподвижная, низшая;

2 - 3 ("В") – вращательная, одноподвижная, низшая;

3 – 4 ("Н₃₄")  – поступательная, одноподвижная, низшая.

Всего кинематических пар 4 и все КП одноподвижные, т.е. р₁ =4.

Двухподвижных КП нет, т.е. р₂ = 0[2].

 Определение числа степеней свободы механизма

Для плоского механизма

W = 3n – 2p₁ – 1p₁ = 3 · 3 – 2 · 4 – 1 · 0 = 1.

W = 1 означает, что достаточно задать движение одному подвижному звену и все звенья получат движение.

Анализ принципа образования механизма

В состав механизма входят две структурные группы:

а) группа начальных звеньев, состоящая из звеньев 1 и 4 с одной вращательной кинематической парой "0" (рисунок 2 а).

Степень подвижности группы

W₁ = 3n – 2p₁ = 3 · 1 – 2 · 1 = 1;

б) группа с нулевой степенью подвижности (группа Ассура), состоящая из звеньев 2 и 3 и трех кинематических пар "А", "В" - вращательные;

"Н₃₄" - поступательная (рисунок 2б). Степень подвижности группы

W' = 3n – 2p₁ = 3 · 2 – 2 · 3 = 0.

Рисунок 2 (а, б) Структурные группы механизма

Таким образом, механизм образован последовательным присоединением к группе начальных звеньев с W = 1 одной двухповодковой группы (диады) Ассура с W = 0 и является механизмом 1 класса 2-го порядка.

Перейдем к кинематическому анализу механизма  Построение плана механизма в 6 – 8 положениях (через 45º или 60º)

Исходные данные: ℓ_ОА = 0,05 м; ℓ_АВ = 0,20 м.

Из условия размещения плана на листе выбирается масштабный коэффициент длины звеньев, например, по звену ОА

К_ℓ = ,

где  – длина отрезка, изображающего длину звена на плане.

С учетом К_ℓ = 0,002 м/мм длина звена АВ на плане:

 =  =  = 100 мм.

В выбранном масштабе вычерчиваются планы механизма (рисунок 3).

Из точки "O" проводится окружность радиусом ОА – траектория движения точки "А", которая делится на 8 равных частей (через 45°), восемь положений кривошипа и горизонтальная линия – траектория движения точки "В".

Точки А нумеруются от 1 до 8 в направлении вращения. Из каждой точки А₁…А₈ на горизонтальной линии, проведённой из точки О отмечаются места положения ползуна В₁…В₈ отсекая их дугой окружности радиусом . На середине каждого отрезка А_nВ_n отмечается точка положения центра масс шатуна S₁… S₈. Соединение этих точек позволяет получить фигуру в виде овала, которая соответствует траектории движения центра масс шатуна S₂.

Траектория движения центра масс шатуна (точки S₂) и  характеристика траекторий движения точек А, В.

По планам механизма (рисунок 3) получена траектория движения центра масс шатуна, которая представляет собой эллипс. Траектория движения точки "А" – окружность, точки "В" (ползуна) – прямая линия. Ползун является рабочим органом, совершает возвратно-поступательное движение из одного  крайнего положения в другое (имеет две мертвые точки).

Рисунок 3. Планы положений механизма

Кинематическая схема механизма в заданном положении

Исходные данные: φ₁ = 45^°; ℓ_ОА = 0,05 м; ℓ_АВ = 0,20 м;

n₁  = 765 об/мин или угловая скорость вращения кривошипа

ω₁ =  =  = 80 рад/с.

В принятом масштабе К_ℓ= 0,002 м/мм кинематическая схема механизма (план механизма) при φ₁ = 45° для анализа изображена на рисунке 4. Планы скоростей (рисунок 5) и ускорений (рисунок 6) построить на том же листе.

Рассмотрим  определение линейной скорости точек А, В; угловой скорости шатунa и их направления

Линейные скорости точек υ_ί механизма определяются из плана скоростей, который строится из полюса плана в масштабе К_υ = , где  - длина отрезка в мм, изображающая скорость точки υ_ί на плане. Скорость точки А: υ_А = ω₁ ℓ_ОА = 80 · 0,05 = 4 м/с. Вектор _А приложен в точке А перпендикулярно звену 1 и направлен в сторону его вращения. Принимаем масштабный коэффициент скорости К_υ = 0,1 . На плане скорость _А изображается отрезком =  =  = 40 мм, отложенным из полюса плана р_υ (рисунок 5). Скорость неподвижной точки О равна нулю. Для определения скорости точки В используем векторное уравнение

                                                                                                           (1)

где  - относительная скорость точки В при вращении вокруг точки А, направлена перпендикулярно звену ВА. С учетом этого

=  +                                                                                                             (2)

 ||ОВ  АОВА.

Векторное уравнение (2) с двумя неизвестными величинами  и  решается путем построения плана скоростей.

Построение плана скоростей производится в следующей последовательности.

Из произвольно выбранного полюса р_υ (рисунок 5) откладываем отрезок  = 40 мм перпендикулярно звену АО, в направлении вращения. Из полюса  р_υ проводится направление вектора параллельно ОВ, а из точки "а" (конца вектора ) проводится направление вектора  перпендикулярно ВА до пересечения с направлением вектора . Пересечение направлений дает точку "в" – конец векторов  и . Измерив по плану отрезки  и  в мм получим:

υ_В = К_υ· = 0,1 · 34 = 3,4 м/с;

υ_ВА = К_υ· = 0,1 · 29 = 2,9 м/с.

Величину угловой скорости шатуна определяем по формуле:

ω₂ = υ_ВА/ℓ_АВ = 2,9/0,2 = 14,5 рад/с;

Для определения направления угловой скорости ω₂ переносим вектор относительной линейной скорости  в точку В плана механизма (рисунок 4) и укажем их направление.

Рисунок 4. Кинематическая схема механизма

 Определение линейного ускорения точек А, В; углового ускорения шатуна и их направления

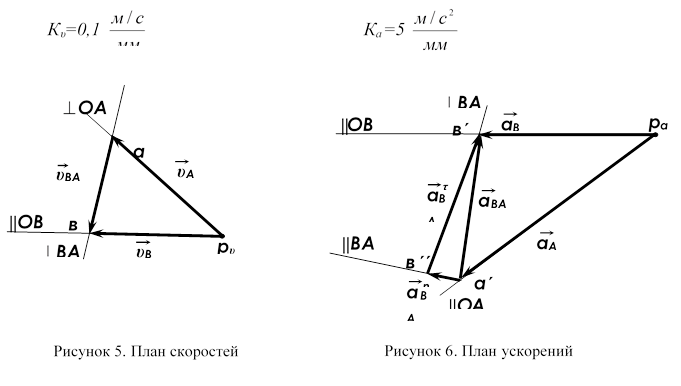
Линейные ускорения характерных точек механизмов (А, В) определяются из плана ускорений, который строится в выбранном масштабе.

Так как звено 1 (ОА) вращается равномерно (ω₁ = 80 рад/с = const), то точка А имеет только нормальное ускорение

а_А =  =  · ℓ_ОА = 80² · 0,05 = 320 м/с².

Принимаем масштабный коэффициент ускорения К_а = 5 .

Вектор  приложен в точке А и направлен вдоль звена АО к центру вращения в точке О. На плане ускорений ускорение  изображается отрезком ´ =  =  = 64 мм, отложенным из полюса плана р_а (рисунок 6).

План ускорений строится по аналогии с планом скоростей, с использованием векторного уравнения:

 =  +  =  +  + ,

где  || ОВ;  || ОА;  || ВА;   ВА.

Нормальная составляющая  равна:

 =  = 14,5 · 0,2 = 42 м/с²

и направлена вдоль линии ВА к центру вращения в точке А.

В масштабе К_а = 5 (м/с²) / мм отрезок, изображающий нормальное ускорение , на плане представлен:  =  =  = 8,4 мм.

Согласно векторному уравнению из точки В´´ проводится линия действия тангенциальной составляющей относительного ускорения  перпендикулярно линии ВА, а из полюса р_а – линия действия абсолютного ускорения точки В параллельно линии ОВ. Точка пересечения этих линий В´ определяет вектор ускорения .

Измерив по плану ускорений соответствующие отрезки, получим:

а_В = К_а ·  = 5 · 46 = 230 м/с²;

 = К_а ·  = 5 · 45 = 225 м/с².

Величина углового ускорения звена 2 определяется по формуле:

ε₂ =  =  = 1125 рад/с².

Для определения направления углового ускорения звена 2 переносим вектор касательной составляющей ускорения  в точку В плана механизма (рисунок 4) и укажем их направление.

В результате структурно-кинематического анализа кривошипно-ползунного механизма в заданном положении φ = 45° установлено:

1. Механизм имеет одну степень подвижности.

2. Траекториями движения характерных точек являются: точки А (кривошипа) – окружность; точки В – прямая линия.

3. Звено 1 (кривошип) движется равномерно-вращательно, звено 2 (шатун) совершает сложное плоскопараллельное равнозамедленное движение, звено (3) – ползун совершает возвратно-поступательное равноускоренное движение.

Данный механизм может найти применение в поршневых машинах (двигателях внутреннего сгорания, компрессорах, насосах, прессах и т.д.).

Разработка индивидуальных заданий, а также проверка выполнения домашних работ осуществляется преподавателем, и результаты учитываются в виде дополнительных баллов, выставляемых студентам  в процессе промежуточной аттестации, о чем они предварительно оповещаются.

Список литературы:

1.     Артоболевский И.И. Теория механизмов и машин. М.: Наука, 1988.

2.     Павлов О.Ю. Механика. Учебное наглядное пособие. Лениногорск, 2014.