НЕЛИНЕЙНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ

NONLINEAR MATHEMATICAL MODELS

Lyubich Artyom Alekseevich

Student, Kuzbass Humanitarian and Pedagogical Institute, Kemerovo State University, Russia, Novokuznetsk

Zagorsky Kirill Pavlovich

Student, Kuzbass Humanitarian and Pedagogical Institute, Kemerovo State University, Russia, Novokuznetsk

Аннотация. Статья посвящена нелинейным математическим моделям. Рассмотрены их основные типы, ключевые свойства, методы исследования и практическая значимость в различных областях знания.

Abstract. The article focuses on nonlinear mathematical models. It examines their main types, key properties, research methods, and practical significance across various fields of study.

Ключевые слова: нелинейные модели, математическое моделирование, динамические системы, устойчивость, линеаризация, численные методы.

Keywords: nonlinear models, mathematical modeling, dynamical systems, stability, linearization, numerical methods.

Математическое моделирование [1] является одним из ключевых инструментов описания сложных процессов в естественных науках, инженерии, экономике и биологии. Важнейшее место среди этих методов занимают нелинейные математические модели, поскольку большинство реальных систем демонстрирует поведение, которое невозможно адекватно описать линейными зависимостями. Нелинейные модели позволяют учитывать насыщение, ограничение ресурсов, экспоненциальный рост, наличие пороговых эффектов и другие особенности, характерные для реальных объектов.

Нелинейной называется математическая модель, в которой связь между переменными не может быть выражена линейной функцией вида y = ax + b. К нелинейным моделям относят случаи, где используются степенные функции, экспоненциальные, логарифмические, рациональные, логистические, а также смешанные типы функций.

Нелинейные модели можно разделить на несколько основных групп. Статические, или алгебраические, модели характеризуют установившиеся зависимости между параметрами системы. Примерами служат вольтамперная характеристика диода

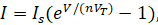
зависимость спроса от цены

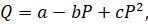
а также различные тепловые и механические нелинейные зависимости

, .

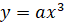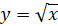Динамические модели [3], описываемые дифференциальными уравнениями, показывают изменение системы во времени. К ним относятся закон охлаждения Ньютона:

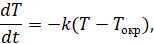
уравнение логистического роста

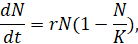
модели зарядки RC-цепи с нелинейным элементом (например, диодом), а также модели накопления средств со сложными процентами и изменяющейся доходностью.

Отдельную важную категорию составляют модели с обратной связью, используемые в экономике, инженерии и экологии. К ним относятся различные регуляторы, автоколебательные системы и классические модели типа «хищник–жертва».

Нелинейные системы обладают рядом особенностей, которые отличают их от линейных. К ним относятся: наличие нескольких решений (система может иметь несколько равновесных состояний); сложная картина устойчивости, когда даже небольшие изменения параметров могут резко изменить поведение; пороговые эффекты, при которых система кардинально меняет режим работы при достижении определённого уровня; эффект насыщения, когда увеличение входного воздействия перестаёт приводить к росту отклика; и нелинейная чувствительность, при которой малое изменение параметра вызывает непропорционально сильную реакцию. Эти особенности делают нелинейные модели одновременно более реалистичными и более сложными для анализа.

Исследование нелинейных математических моделей является более сложной задачей по сравнению с линейными, поскольку аналитические решения таких моделей существуют далеко не всегда. В связи с этим разработан широкий спектр методов анализа.

Графический метод является первым и наиболее наглядным шагом исследования нелинейной зависимости. Он позволяет визуально оценить форму функции, определить наличие экстремумов, выявить точки насыщения или перегиба, а также определить диапазон изменения выходных переменных. Для динамических моделей, описываемых дифференциальными уравнениями, часто используют фазовые портреты - графики, отражающие траекторию системы в пространстве состояний. Такие графики позволяют увидеть циклы, стремление к равновесию, а также оценить устойчивость или неустойчивость решений.

Когда точное аналитическое решение недоступно, широко применяется метод линеаризации. Поведение системы около точки равновесия можно описать, аппроксимировав её линейной моделью. Суть метода заключается в нахождении стационарной точки x₀ и разложении функции в ряд Тейлора около этой точки с сохранением только первого порядка малости: f(x) ≈ f(x₀) + f'(x₀)(x - x₀). Линеаризация особенно востребована в инженерных системах управления, моделировании электроцепей и экономических моделях с малым отклонением параметров от нормы, так как позволяет оценивать устойчивость и характер отклика системы на малые возмущения.

Одной из ключевых задач в нелинейных моделях [2] является определение устойчивости равновесных состояний. Именно этот параметр показывает, как система ведёт себя при малых отклонениях: возвращается ли к устойчивому равновесию, наращивает ли отклонения в случае неустойчивости или демонстрирует полуустойчивое поведение. Для анализа устойчивости используют знак производной в статических моделях, собственные значения матрицы Якоби в многопараметрических системах, метод Ляпунова в сложных кинетических моделях и анализ фазовых диаграмм. Этот метод широко применяют при исследовании популяций, моделей распространения инфекции, электронных схем и любых процессов с обратными связями [5].

В большинстве случаев нелинейные уравнения и системы не имеют аналитического решения, поэтому используются численные методы [6]. К ним относятся метод последовательных приближений и метод Ньютона для нахождения корней алгебраических уравнений. Для решения дифференциальных уравнений применяют метод Эйлера, усовершенствованный метод Эйлера и семейство методов Рунге–Кутты, которые являются наиболее популярными. Численные методы стоят в основе всех компьютерных симуляторов, начиная от моделирования климата и заканчивая расчётом электрических схем. Нелинейные модели находят широкое применение в технике, например моделирование электронных компонентов, термодинамика, в экономике это анализ спроса, оптимизация прибыли, модели финансовых рынков, в биологии участвует в росте популяций, взаимодействие видов, в физике используется в механике, колебаниях, теплопередач и в химии кинетика реакций с насыщением. Именно нелинейность позволяет моделировать ключевые реальные эффекты: экспоненциальный рост, насыщение, пороговый переход и резкие изменения поведения системы [4]. Таким образом, нелинейные математические модели являются важнейшим инструментом анализа сложных процессов, встречающихся в природе, технике и экономике. Они позволяют описывать системы, поведение которых невозможно представить в виде простой пропорциональной зависимости. Понимание структуры и свойств нелинейных моделей, а также владение методами их анализа - графическими, численными и аналитическими - позволяет эффективно применять их в различных областях знания для изучения реальных процессов.