Граничное интегральное представление полигармонической функции

The boundary integral representation of polyharmonic function

Anastasiya Kazakova

Candidate of Physical and Mathematical Sciences, associate professor, The Ulianov Chuvash State University, Russia, Cheboksary

Аннотация. На основании интегральной формулы Грина получено представление n-гармонической функции в области T через граничные значения полигармонических функций более низких порядков и их нормальных производных. В осесимметричной пространственной области выполнен переход к контурным интегралам по образующей граничной поверхности. Проведено исследование функций, входящих в полученные представления.

Abstract. The integral representation of n-harmonic function through the boundary values of lower-order polyharmonic functions and their normal derivatives is obtained by using the integral Green formula. In an axisymmetric spatial domain the transition to contour integrals along the generatrix of the boundary surface is performed. The functions entering into the received representations are investigated.

Ключевые слова: интегральная формула Грина; полигармоническое уравнение; функция Грина; краевые задачи; метод граничных элементов; логарифмиче­ская особенность.

Keywords: integral Green formula; polyharmonic equation; Green function; boundary-value problem; boundary element method; logarithmic singularity.

При изучении свойств гармонических функций, а также при разработке численных методов эффективно применение интегральной формулы Грина, которая для плоской области T имеет вид:

 ,                                                                                       (1)

где Δ – оператор Лапласа.

Из формулы (1) можно получить важную формулу, дающую выражение значения функции в любой точке  в плоской области T:

 ,                                                                                 (2)

где функция Грина для плоской области, расстояние от фиксированной точки  до переменной точки интегрирования.

Если гармоническая функция, то второе слагаемое правой части (2) обращается в нуль, и соотношение выражает значение функции  в любой внутренней точке области T через ее значения на границе. С помощью (2) были разработаны численные алгоритмы для гармонических уравнений, основанные на методе граничных элементов [1], что позволило рассчитать широкий круг задач механики сплошных сред [5], [4]. Аналогичный подход может быть применен и для решения краевых задач для полигармонического уравнения. Однако в этом случае второе слагаемое правой части содержит двойной интеграл. В настоящей работе для случаев плоской и осесимметричной пространственной области T формула (2) для полигармонической функции u преобразована к виду, содержащему только контурные интегралы.

Интегральное представление полигармонической функции в плоской области

Пусть функция  есть частное решение уравнения

  , .                                                                                                   (3)

Решение уравнения (3) может быть найдено интегрированием k-кратного оператора Лапласа в полярных координатах. Рассмотрим сначала случай :

 ,                                                                                              (4)

откуда, полагая константы интегрирования равными нулю,

.

Далее, при  уравнение (3) примет вид , , откуда:

               .

Продолжая аналогично далее, получим следующую формулу:

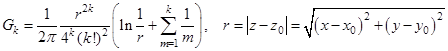.                                                                          (5)

Пусть полигармоническая функция n-го порядка, т.е. удовлетворяет дифференциальному уравнению . Введем обозначения:

 .                                                                                       (6)

Обратимся к уравнению (2) и рассмотрим второе слагаемое в его правой части. Интеграл  по области T можно представить в виде

.

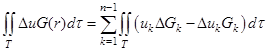На основании формулы Грина (1) интегралы в правой части последнего равенства представляются через контурные интегралы:

,

где оператор дифференцирования по внешней нормали.

Поэтому для второго слагаемого правой части (2) имеем окончательно:

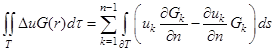                                .                                                                                       (7)

Подставляя (7) в (2), получим окончательно, что значение полигармонической функции внутри области выражается через граничные значения функций  и их нормальных производных по формуле:

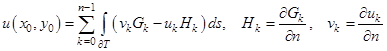                     .                                                                           (8)

С помощью формулы (8) можно получить решение основной краевой задачи для полигармонического уравнения [3].

Интегральное представление полигармонической функции в осесимметричной пространственной области

Формула (8) справедлива и в случае, если область T является трехмерной. При этом правая часть (8) будет представлять собой сумму поверхностных интегралов, функция Грина для пространственной области,

                                      , .                                                                                           (9)

Пусть поверхность граница области T. Тогда формула (8) примет вид

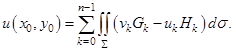                                                                                                                           (10)

Если поверхность  является осесимметричной и функции   обладают осевой симметрией, то поверхностные интегралы в (10) можно свести к контурным интегралам по образующей  поверхности . В цилиндрических координатах  функции  и  не зависят от , поэтому  из (10) следует

                                      .                                                                                      (11)

где расстояние от оси области T до переменной точки интегрирования,

                                     .                                                                                          (12)

Далее определим вид функций (12). Из (9) и (12) следует, что:

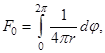
                                                                                                (13)

Цилиндрические координаты можно выбрать так, чтобы , поэтому

                       , .                                                                           (14)

Замена  сводит (14) к полному эллиптическому интегралу I рода :

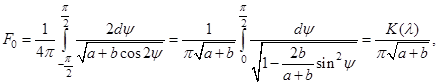
                                                                (15)  

Так как производная , то

                                                                                  (16)

Здесь полный эллиптический интеграл II рода. Насколько нам известно, впервые функции вида (15), (16) в иной форме получены в [2].

С помощью той же замены найдем функцию . После соответствующих преобразований, учитывая, что , имеем:

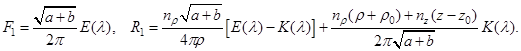                                                                       (17)

Для функций  можно получить рекуррентную формулу. Из (12)

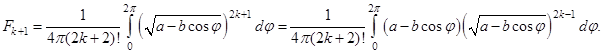
Последний интеграл можно разложить на сумму двух интегралов, первый из которых содержит функцию , а второй можно представить в виде

                                                                    (18)

Можно заметить, что первообразной в последнем интеграле является , и, следовательно, он обращается в нуль. Поскольку

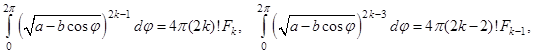
то функции

,

или, после сокращения и приведения слагаемых к общему знаменателю,

                                                                                                                (19)

Рекуррентное соотношение для нормальных производных имеет вид:

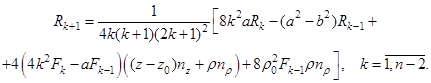                                                                                (20)

Исследование функций, входящих в интегральные представления полигармонической функции

Выясним вопрос об особенностях функций, входящих в (8) и (11), при
. В плоском случае речь идет о функциях вида (5) и их нормальных производных. Из (5) видно, что среди функций  только функция  имеет особенность (логарифмическую); для остальных функций 

   .

Вид функций  также получается непосредственно из (5). В частности,

                                                                   (21)

Исследуем поведение этой функции при . Пусть граница области  задана функциями дуговой координаты , . Тогда  и . В окрестности точки  (, ) имеем

Тогда можно считать, что (, , , )

 , .

В ряды в окрестности  можно разложить и компоненты нормали:

Тогда для функции  будем иметь

  .

Рассмотрим далее функцию

Функция  при  () стремится к нулю и не имеет в этой точке особенность. Это справедливо и для остальных функций  ().

Теорема 1. В плоском случае из всех функций , , входящих в интегральное представление для полигармонической функции, только функция  имеет особенность в точке  (), а именно логарифмическую, т.е. интегрируемую, особенность.

Проведем теперь исследование функций (12), входящих в представление (11). Пусть функции  определяют образующую , а  и – дуговые координаты точки интегрирования и фиксированной точки на . Исследуем поведение функций  при . Тогда , и можно показать, что  при . Так как , то .

Разложим функцию  в ряд в окрестности этой точки (, ):

В окрестности точки : , поэтому при достаточно близких к единице значениях  можно считать, что

                                                                                                                                    (22)

Подставляя в (22)  и учитывая, что , получим:

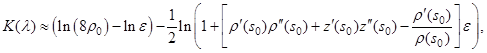
или, с учётом разложения в ряд Маклорена последнего слагаемого,

                                                                                            (23)

Выражение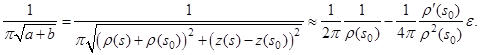 

Перемножим почленно последнее выражение и правую часть (23), тогда

откуда видно, при    имеет логарифмическую особенность.

Так как , то . Согласно рекуррентной формуле (19),

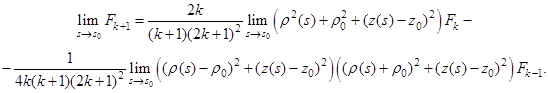
А так как второй предел, очевидно, равен нулю, то оказывается, что

 .

Исследуя функции  и используя формулу (20), можно получить, что

причём в окрестности точки 

Если положить  () и разложить в ряды компоненты вектора нормали в окрестности точки , то получим окончательно

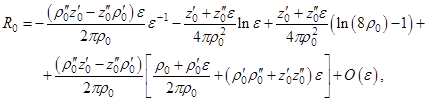
откуда видно, что  имеет в точке  логарифмическую особенность.

Теорема 2. В пространственном осесимметричном случае из всех функций , , входящих в интегральное представление для полигармонической функции, только функции ,  имеют особенность в точке  (), а именно обе логарифмическую, т.е. интегрируемую, особенность.

Заключение

Получены интегральные представления n-гармонической функции в плоской и в осесимметричной пространственной области через граничные значения полигармонических функций более низких порядков и их нормальных производных. В случае осесимметричной пространственной области осуществлен переход к контурным интегралам по образующей граничной поверхности. Полученные представления, а также проведенное в данной работе исследование входящих в них функций, могут оказаться полезными при разработке численных методов решения краевых задач для полигармонического уравнения.