Анализ резонансного преобразователя постоянного напряжения типа LLC

Analysis of the LLC Resonant DC-DC Converter

Gennady Belov

Doctor of Science, Professor, The Ulianov Chuvash State University, Russia, Cheboksary

Grigory Ohotkin

Doctor of Science, Associate Professor, The Ulianov Chuvash State University, Russia, Cheboksary

Anfisia Pavlova

Senior Lecturer, The Ulianov Chuvash State University, Russia, Cheboksary

Аннотация. Рассмотрен резонансный преобразователь постоянного напряжения (ППН) типа LLC, которому в зарубежной литературе уделяется большое внимание. Методом основной гармоники выведены основные расчётные соотношения для ППН с учётом активных сопротивлений LC-контура и использованием широко распространённой в отечественной литературе Т-образной эквивалентной схемы трансформатора. Учёт активных сопротивлений потерь позволил получить выражение для расчёта КПД преобразователя, отсутствующее в зарубежных публикациях. Известные из зарубежных публикаций расчётные соотношения получаются как частные случаи выведенных в предлагаемой статье.

Abstract. The LLC resonant DC-DC converter is considered, which is paid much attention in the foreign literature. By basic harmonic method, the main calculation ratios for DC-DC converter with allowance for the active resistances of the LC circuit and the use of the T-shaped equivalent circuit of the transformer widely used in the domestic literature are derived. Taking into account the active resistance of losses, it was possible to obtain an expression for calculating the converter efficiency, which is absent in foreign publications. Known from foreign publications, the calculated relationships are obtained as special cases derived in the proposed article.

Ключевые слова: резонансный преобразователь постоянного напряжения; условия резонанса; коэффициент передачи для индуктивного и ёмкостного режимов.

Keywords: DC-DC resonant converter; resonance conditions; transmission coefficient for inductive and capacitive modes.

Резонансные LLC преобразователи постоянного напряжения (ППН) отличаются возможностью получения высокого КПД, малых габаритов и массы при сравнительно высоких рабочих частотах. Резонансные ППН, работающие в режиме прерывистого тока в LC-контуре, когда индуктивность намагничивания трансформатора L_µ по крайней мере на два порядка превышает индуктивность рассеяния , были подробно рассмотрены ранее [1]. В настоящее время широко используются преобразователи, в которых индуктивность рассеяния соизмерима с индуктивностью намагничивания [2, 3].

Наиболее простым методом анализа и расчёта таких преобразователей является метод основной гармоники [4], который основан на предположении о том, что передача энергии от источника входного напряжения u_вх к нагрузке R через резонансный контур обусловлен первыми гармониками вызываемых в контуре напряжений и токов. Тогда ток в резонансном контуре i_к полагается чисто синусоидальным. Такой подход дает близкие к точным результаты при работе выше резонансной частоты в режиме непрерывного тока контура и весьма приближённые результаты на частотах переключений ниже резонансной (в режиме прерывного тока). Следует отметить, что при использовании метода основной гармоники многие детали работы схемы на периоде переключений будут потеряны.

Предположим, что каждый из транзисторов VT1, VT2 несимметричной полумостовой схемы (рисунок 1, а) открывается на полпериода в противофазе с другим. Выходное напряжение u_и (рисунок 1, б) инверторного полумоста (рисунок 1, а) может быть представлено в виде ряда Фурье [5]

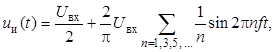
где f = 1/T – частота переключений, первая гармоника (n = 1)

                                                                                                                                                   (1)

Ток в резонансном контуре  где I_к – действующее значение тока контура, φ – фазовый сдвиг тока относительно первой гармоники напряжения u_и(1)(t). Этот ток отстает от напряжения u_и(1)(t) на угол φ > 0, если общее сопротивление контура носит индуктивный характер (индуктивный режим) (когда частота переключений больше резонансной частоты контура f_р), и опережает напряжение на угол φ < 0 при ёмкостном характере общего сопротивления контура (ёмкостной режим) (f < f_р).

Через источник входного напряжения u_вх протекает входной ток i_вх (рисунок 1, б), равный току контура на интервале T/2, когда проводит верхний транзистор VT1 (рисунок 1, а). В следующий полупериод входной ток равен нулю. Среднее значение входного тока определяется следующим образом:

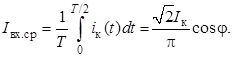
Тогда активная мощность, потребляемая от источника входного напряжения, определяется выражением , где согласно (1) величина  представляет собой действующее значение первой гармоники выходного напряжения инвертора.

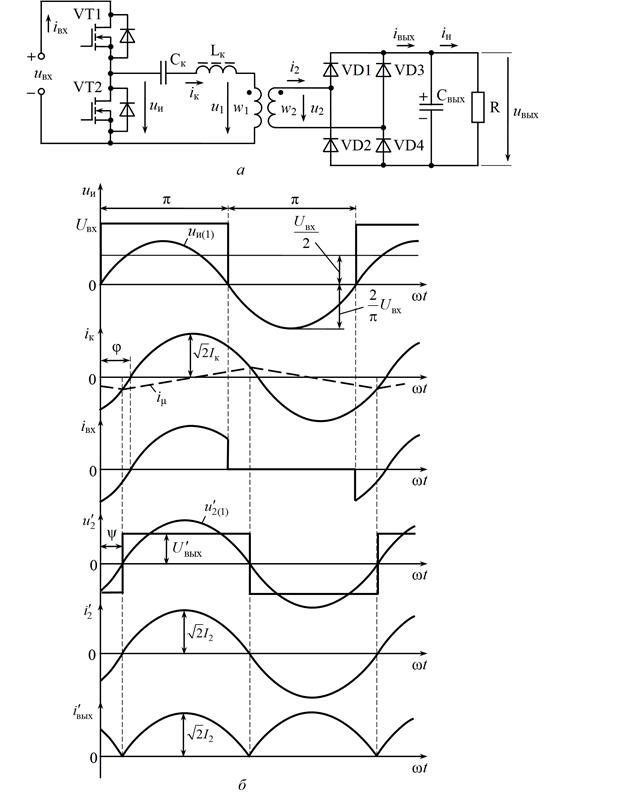
Рисунок 1. Схема силовой части несимметричного полумостового резонансного преобразователя (а);  временные диаграммы, иллюстрирующие работу преобразователя в установившемся режиме (б)

Диоды VD1, VD4 выходного выпрямителя открываются в момент перехода тока во вторичной обмотке трансформатора через нуль с отрицательного значения на положительное, а диоды VD2, VD3 – в момент перехода тока во вторичной обмотке через нуль с положительного значения на отрицательное. Если не учитывать ток намагничивания трансформатора i_µ , эти моменты совпадают с моментами перехода через нуль тока i_к резонансного контура. В реальной схеме отпирание диодов выпрямителя и изменение полярности напряжения на вторичной обмотке u₂ происходят при переходе через нуль тока вторичной обмотки трансформатора, приведенное к первичной обмотке значение которого равно , где i₁ = i_к – ток в первичной обмотке трансформатора, совпадающий с током LC-контура i_к . В свою очередь, изменение тока намагничивания i_µ связано с напряжением .

Напряжение на вторичной обмотке трансформатора u₂ с учётом рисунка 1, б может быть представлено в виде ряда Фурье [5]

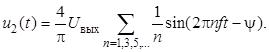
Первая гармоника этого напряжения определяется выражением

                                                                                                                                       (2)

где ψ – фазовый сдвиг первой гармоники относительно напряжения u_и(1)(t), выходное напряжение преобразователя u_вых принимается идеально сглаженным, u_вых = U_вых = const.

Полагая ток i₂ синусоидальным и совпадающим по фазе с первой гармоникой напряжения на вторичной обмотке u₂₍₁₎ , найдем среднее значение выходного тока, совпадающее со средним значением тока нагрузки I_н.ср ,     

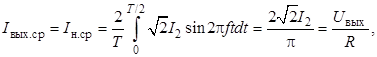
где I₂ – действующее значение тока i₂ . Из этого равенства найдем

                                                                                                                                                                (3)

Поскольку напряжение u₂₍₁₎(t) и ток i₂(t) находятся в фазе, входное сопротивление выходного выпрямителя на частоте переключений с учётом конденсатора C_вых и сопротивления нагрузки R является чисто активным. С учётом (2) и (3) найдем это входное сопротивление        

Имеем также очевидное равенство для выходной мощности

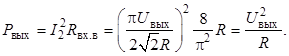
С учётом изложенного получаем линейную эквивалентную схему преобразователя для первых гармоник токов и напряжений (рисунок 2). Здесь принята Т-образная эквивалентная схема трансформатора, в то время как во многих работах вся индуктивность рассеяния трансформатора  считается сосредоточенной на первичной стороне и не учитываются активные сопротивления обмоток r₁ и  [2, 3].

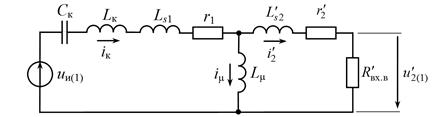
Рисунок 2. Эквивалентная схема преобразователя для первых гармоник токов и напряжений

Операторное входное сопротивление преобразователя (LC-контура) со стороны выходных зажимов инверторного полумоста

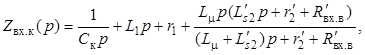                                                                                                    (4)

где L₁ = L_к + L_s1 – суммарная индуктивность цепи первичной обмотки.

Передаточная функция схемы на рисунке 2 определяется выражением

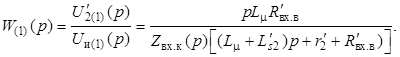                                                                                            (5)

Выражение (4) при подстановке p = jω представляется в виде

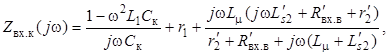
выделяя действительную r_к и мнимую X_к части из которого получаем

                                                                                                                                                   (6)

где

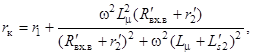
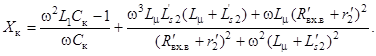
Введя относительные параметры

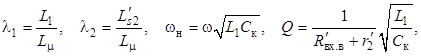
получим

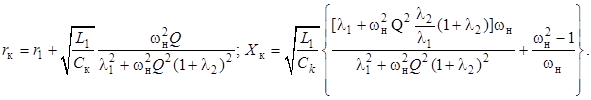                                                     (7)

Найдем нормированную резонансную частоту LC-контура из уравнения X_к = 0. С учётом (7) можем получить биквадратное уравнение          

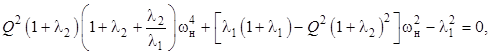                                                                             (8)

откуда следует квадрат нормированной резонансной частоты

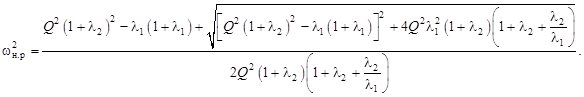                                                             (9)

Знание резонансной частоты важно, поскольку она дает границу между ёмкостным и индуктивным режимами LC-контура: ниже резонансной частоты сопротивление Z_вх.к(jω) имеет ёмкостной характер, выше – индуктивный.

Решая уравнение (8) относительно Q², найдем условие резонанса в виде

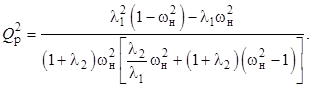                                                                                                                 (10)

Частотная передаточная функция LC-контура получается из (5) при p = jω:

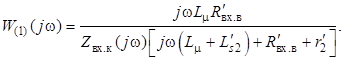
Модуль частотной передаточной функции с учётом (6) принимает вид 

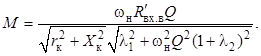
Отсюда с учётом выражений (7) получим

,

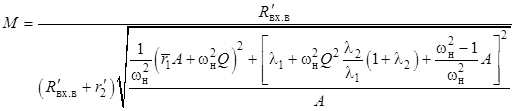где введены обозначения

Это выражение преобразуется к виду

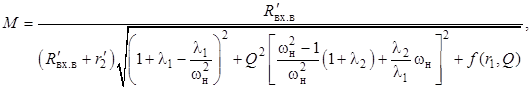                                                                           (11)

где f (r₁ , Q) – функция, зависящая от r₁ и определяемая выражением

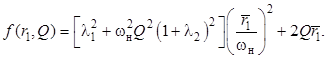
Подставив выражение (10) в равенство (11), после преобразований получим коэффициент передачи при резонансе

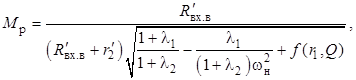                                                                                                           (12)

где функция f (r₁, Q), оказывающая незначительное влияние, не преобразована.

В статьях [2, 3] используется схема замещения трансформатора, в которой не учитываются активные сопротивления обмоток трансформатора и считается, что вся индуктивность рассеяния сосредоточена в цепи первичной обмотки. При таких допущениях в полученных выражениях необходимо принять , . Тогда получаемые выражения совпадают с известными из [2].

При этом формулы (7) для расчёта действительной и мнимой частей сопротивления Z_вх.к(jω) упрощаются к виду

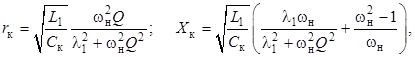                                                                                            (13)

формула (9) для расчёта квадрата нормированной резонансной частоты принимает вид

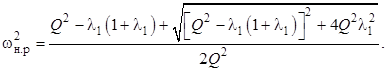                                                                                                    (14)

На рисунке 3 представлены построенные по формуле (14) зависимости нормированной резонансной частоты контура ω_н.р от Q при различных значениях λ₁ . Из (14) следует, что при коротком замыкании нагрузки (Q → ∞) нормированная резонансная частота ω_н.р = 1.

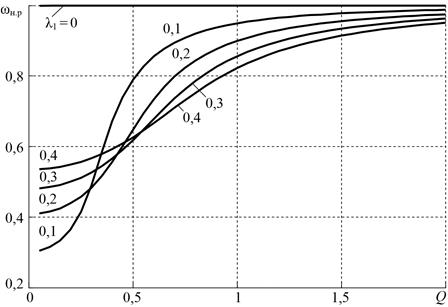
Рисунок 3. Кривые для определения нормированной резонансной частоты

Формула (10) при λ₂ = 0 принимает известный из [2] вид

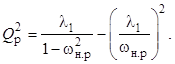
При резонансе сопротивление контура становится чисто вещественным, которое с учётом выражений (13) и (14) принимает вид

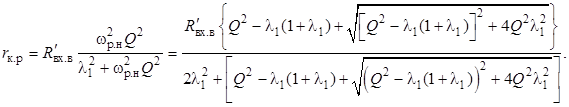
Формула (11) для модуля частотной передаточной функции при  также упрощается:

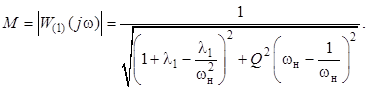                                                                                                  (15)

На рисунке 4 представлены зависимости коэффициента передачи  от нормированной частоты переключений ω_н при различных значениях Q и постоянном λ₁ = 0,2. Как видно из (15), при ω_н = 1 имеем  независимо от значений Q. Это значение  соответствует индуктивному характеру сопротивления контура, когда ток i_к отстает по фазе от напряжения u_н(1) , что является необходимым условием переключений при нулевом значении напряжения на транзисторе (ПНН) [2]. В работе [2] приведены подобные зависимости также при λ₁ = 0,3; 0,5; 0,9, которые показывают влияние параметра λ₁ на характер этих зависимостей и могут быть использованы при выборе значения λ₁ в ходе проектирования преобразователя. Максимумы этих характеристик находятся в ёмкостной области.

Обратим внимание на то, что коэффициент передачи M в индуктивной области уменьшается с ростом частоты ω_н .

Упрощенная формула для расчёта коэффициента передачи при резонансе получается из (12) подстановкой  и :

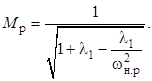
График этой зависимости для λ₁ = 0,2 представлен на рисунке 4 штриховой линией. Эта кривая является границей между индуктивным и ёмкостным режимами LC-контура: если точка (ω_н , M) располагается правее этой кривой, то входное сопротивление контура является индуктивным, в противном случае – ёмкостным.

Коэффициент передачи при резонансе можно определить также, полагая в общем выражении . Тогда получим

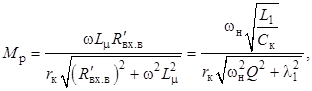
откуда с учётом выражения (13) для r_к найдем

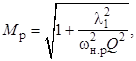
а с учётом выражения (14) –

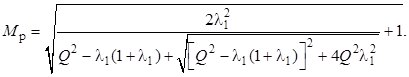
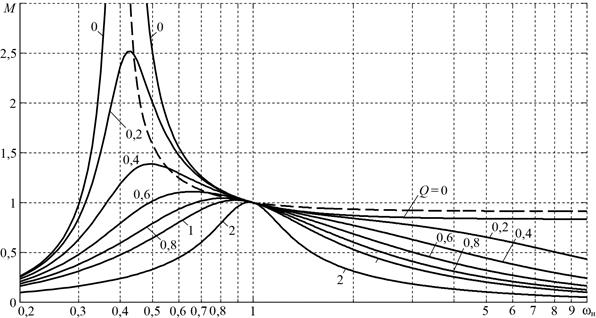
Рисунок 4. Регулировочные характеристики преобразователя для λ₁ = 0,2

В состоянии без нагрузки, когда  индуктивность LC-контура равна L₁ + L_µ , резонансная частота определяется выражением

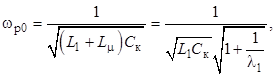
а нормированная резонансная частота при холостом ходе

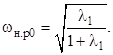
Модуль частотной передаточной функции для рассматриваемой схемы (рисунок 2) при , , , ,  имеет вид

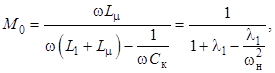                                                                                                                        (16)

что совпадает с выражением, получаемым из (15) при Q = 0.

Подстановка Q = 0 в выражение (14) приводит к неопределенности типа 0/0, хотя решение уравнения, получаемое из (14) при подстановке ω_н = ω_н.p0 , дает значение Q = 0 независимо от значения λ₁ .

Найдем КПД преобразователя. Активную входную мощность P_вх будем определять как действительную часть комплексной входной мощности

где  – комплексно сопряженная величина для тока , определяемого по формуле

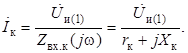
Величину  будем полагать чисто вещественной. Тогда сопряжённый ток

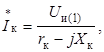
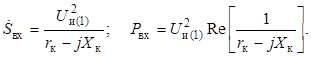
Выходная мощность и КПД определяются равенствами

  ,   

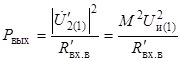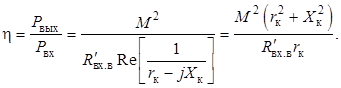
Учитывая выражение

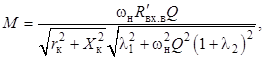
получим расчётное соотношение

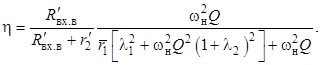                                                                                                                 (17)

На рисунке 5 представлены зависимости, построенные по формуле (17) при , λ₁ = 0,2, λ₂ = 0, а также экспериментальные точки, взятые из [3].

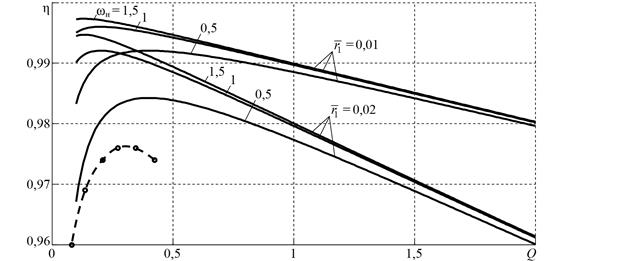
Рисунок 5. Зависимость КПД от «добротности» без учёта потерь в выходном выпрямителе, экспериментальные токи

Список литературы:

1.     Белов Г.А. Высокочастотные тиристорно-транзисторные преобразователи постоянного напряжения. – М.: Энергоатомиздат, 1987. – 120 с.

2.     Silvio De Simone. LLC Resonant Half-Bridge Converter Design Guideline. Application Note AN2450. – 2014. – www.st.com.

3.     Sam Abdel-Rahman. Resonant LLC Converter: Operation and Design. Application Note AN2012-09. – 2012. – Infineon Technologies North America (ITNA) Corp. – www.infineon.com.

4.     Забродин Ю.С. Промышленная электроника. Учеб. для вызов. – М.: Высшая школа, 1982. – 496 с.

5.     Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М.: Наука, 1967. – 608 с.